
Ташлыкова-Бушкевич - Физика. В 2 ч. Ч. 2. Оптика. Квантовая физика. Строение и физические свойства вещества (2014)
.pdf
С увеличением же энергии (т.е. с ростом квантового числа п) максиму-
2
мы распределения ψn(x) располагаются все ближе друг к другу. При
2
очень больших значениях п картина распределения ψn(x) практически «сливается» и распределение представляется равномерным. Следовательно, вероятность обнаружения частицы в разных точках потенциальной «ямы» становится одинаковой.
Отметим, что при возрастании квантового числа п энергетический спектр частицы в бесконечно глубокой потенциальной «яме» изменяется. Дискретность энергетического спектра будет играть все меньшую роль изза уменьшения отношения En к En (26.22б) ( En En ≈ 2
En ≈ 2 n ). Данный результат согласуется с принципом соответствия.
n ). Данный результат согласуется с принципом соответствия.
26.10. Гармонический осциллятор (результаты решения)
Линейным гармоническим осциллятором в классической механике называется система, совершающая колебательное периодическое движение под действием квазиупругой силы около положения устойчивого равновесия, описываемое уравнением вида (7.7) (см. подтему 7.2 ч. 1). Данная система является моделью, используемой при описании классических и квантовых систем. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов.
Согласно классической механике одномерный осциллятор совершает гармонические колебания с циклической частотой ω0 = κ m, где κ – постоянная квазиупругой силы. Поэтому потенциальная энергия одномерного гармонического осциллятора (см. формулу (7.19) ч. 1) может быть определена как
m, где κ – постоянная квазиупругой силы. Поэтому потенциальная энергия одномерного гармонического осциллятора (см. формулу (7.19) ч. 1) может быть определена как
|
κx2 |
mω02 x2 |
|
||
U = |
= |
|
. |
(26.24) |
|
2 |
|||||
|
2 |
|
|
||
Графиком функции (26.24) является парабола (рис. 26.6).
Поскольку потенциальная энергия (26.24) обращается в бесконечность при x → ±∞, то классическая частица может совершать лишь строго финитное движение. Классический осциллятор не может выйти
за |
пределы потенциальной «ямы» |
с |
координатами – xmax ≤ x ≤ xmax, |
где – xmax, xmax – координаты точек поворота, в которых E =U . Частица
U (x)
n = 2  E2 = 5 ω0
E2 = 5 ω0  2 n=1
2 n=1  E1 = 3 ω0
E1 = 3 ω0  2
2
n = 0 |
E0 = ω0 2 |
0Х
Рис. 26.6. График функции U(х), определяющей потенциальную энергию гармонического осциллятора
91

может двигаться только в области, где E ≥U, т.е. между точками поворота.
В квантовой теории задача о квантовом гармоническом осцилляторе сводится к задаче о движении частицы массой т в параболической потенциальной «яме» (26.24). Уравнение Шрёдингера (26.15) для одномерного квантового осциллятора при этом записывается так:
d2ψ |
|
2m |
|
mω02 x2 |
|
||
|
+ |
|
(E − |
|
)ψ = 0, |
(26.25) |
|
dx2 |
2 |
2 |
|||||
|
|
|
|
||||
где Е – полная энергия осциллятора. В уравнении (26.25) ω0 имеет смысл циклической частоты классического одномерного осциллятора. Для этого уравнения, как можно доказать, собственные значения энергии
|
|
1 |
|
n = 0, 1, 2, ... . |
|
|
En |
= n+ |
|
|
ω0, |
(26.26) |
|
|
||||||
|
|
2 |
|
|
|
|
Таким образом, энергия квантового осциллятора в отличие от классического не может быть произвольной, а квантуется (может иметь лишь дискретные значения). Разность энергии между соседними уровнями определяется как
E = En+1 − En = ω0.
Следовательно, уровни энергии квантового осциллятора расположены через равные интервалы ω0 и называются эквидистантными (рис. 26.6).
При n = 0 из выражения (26.26) определяется энергия нулевых колеба-
1
ний (нулевая энергия), равная E0 = 2 ω0, которая была оценена в подте-
ме 26.3 на основе соотношения неопределенностей. Минимальная энергия квантового осциллятора лежит выше минимума потенциальной энергии U = 0 . Квантовый эффект неравенства нулю E0 осциллятора – это следствие соотношения неопределенностей. Наличие нулевой энергии подтверждается экспериментально, например в опытах по рассеянию света кристаллами при низких температурах.
Правилами отбора в квантовой механике называются условия, накладываемые на изменения квантовых чисел при разрешенных переходах системы из одного состояния в другое. Точный расчет, выходящий за рамки данного курса, показывает, что правила отбора для квантового гармонического осциллятора имеют вид
n = ±1, |
(26.27) |
92

т.е. возможны лишь переходы между соседними уровнями энергии (рис. 26.6). Следовательно, энергия гармонического осциллятора в излучательных процессах может изменяться только порциями ω0 : гармонический осциллятор испускает и поглощает энергию квантами.
Решения уравнения (26.25) таковы, что имеется отличная от нуля вероятность обнаружить частицу за пределами области – xmax ≤ x ≤ xmax, т.е. в классически запрещенной области, где E <U . Существование отличных
от нуля значений |
|
ψn(x) |
|
2 |
за пределами потенциальной «ямы» объясняет- |
||
|
|
||||||
|
|
|
|||||
ся волновыми свойствами микрочастиц. |
|||||||
Квантовая плотность |
вероятности |
ψn(x) |
2 |
||||
обнаружения частицы |
|||||||
(квантового гармонического осциллятора) в окрестности точки х зависит от значения квантового числа п (рис. 26.7).
При малых значениях квантового числа функции |
|
ψn(x) |
|
2 |
||||
|
|
|||||||
|
|
имеют ко- |
||||||
нечные значения в области |
|
x |
|
≥ xmax и принципиально |
|
отличаются |
||
|
|
|
||||||
от плотности вероятности обнаружения классического осциллятора (пун-
ктирная линия на рис. 26.7, б). С ростом числа п функция |
|
ψn(x) |
|
2 |
прибли- |
||||
|
|
||||||||
|
|
|
|||||||
жается к классической кривой распределения. При n → ∞ график |
|
|
ψn(x) |
|
2 |
||||
|
|
||||||||
|
|
|
|
||||||
переходит в классическую функцию распределения плотности вероятности.
а |
|
б |
в |
|
ψ0 |
2 |
ψ1 2 |
ψ2 |
2 |
|
n = 0 |
n =1 |
|
n =2 |
− xmax0 xmax Х |
− xmax |
|
0 |
xmax Х |
− xmax |
0 |
xmax Х |
Рис. 26.7. Плотности вероятности |
ψn |
2 |
для квантового осциллятора при значениях глав- |
||||
ного квантового числа n = 0,1, 2 . Случай классического осциллятора показан для n = 1 |
|||||||
Рассмотренная модель гармонического осциллятора и связанная с ним задача о движении частицы в параболической потенциальной «яме» является идеализацией, которая справедлива только при малых отклонениях колеблющейся частицы от положения равновесия. В реальных системах потенциальная энергия U частицы, совершающей колебания около положения равновесия, имеет более сложный вид. При возрастании амплитуды колебаний движение частицы будет все больше усложняться, отличаясь от гармонических колебаний. Такое движение называют ангармоническим движением, а соответствующий осциллятор – ангармоническим осциллятором.
93
26.11. Прохождение частицы через одномерный потенциальный барьер
Если поместить частицу в потенциальную «яму» с конечной высотой стенок, то с точки зрения законов классической физики она может выйти из этой «ямы» лишь при условии, что ее полная энергия превышает глубину потенциальной «ямы». То есть частица, находящаяся внутри потенциальной «ямы», «заперта» в ней.
В квантовой механике существует принципиальная возможность прохождения («просачивания») частиц сквозь потенциальные барьеры. Это явление называется туннельным эффектом. Для его описания вводится понятие коэффициента прозрачности (пропускания) D потенциального барьера:
D = |
Iпрох |
= |
jпрох |
, |
(26.28) |
|
|
j |
|||||
|
I |
пад |
|
|
|
|
|
|
|
пад |
|
|
|
где Iпрох и jпрох – соответственно интенсивность дебройлевской волны, прошедшей барьер, и плотность потока частиц, прошедших барьер; Iпад и jпад – соответственно интенсивность волны де Бройля, падающей на барьер, и плотность потока частиц, падающих на барьер.
Коэффициент прозрачности D можно рассматривать как вероятность преодоления частицей потенциального барьера. Из обратимости по времени следует, что для переходов в «прямом» и «обратном» направлениях коэффициенты прозрачности одинаковы.
Аналогично можно определить коэффициент отражения барьера R как вероятность того, что поток частиц (частица) отразится от барьера:
R = |
Iотр |
= |
jотр |
, |
(26.29) |
|
|
j |
|||||
|
I |
пад |
|
|
|
|
|
|
|
пад |
|
|
|
где Iотр и jотр – соответственно интенсивность волны де Бройля, отразившейся от барьера, и плотность потока частиц, отразившихся от барьера и полетевших в обратном направлении. Расчеты показывают, что прозрачность барьера зависит от его «формы» и высоты.
Таким образом, согласно определению, R + D =1. Кроме того, значения R и D не зависят от направления движения частицы.
Существуют два простейших варианта одномерных потенциальных барьеров – прямоугольный потенциальный барьер в виде ступеньки, когда потенциальная энергия U при х = 0 скачком изменяется на конечную величину U0, а также потенциальный барьер прямоугольной формы высотой U0 и шириной l (рис. 26.8, а, б). Потенциальная энергия определяется соответственно так:
94

а |
|
|
б |
|
|
|
Е1 |
U |
|
|
U |
|
|
|
|
Е U0 |
|
|
||
Е2 |
U |
|
|
|
||
0 |
|
1 |
2 |
|
3 |
|
|
1 |
2 |
|
|||
|
|
|
|
|
||
|
0 |
|
Х |
0 |
l |
Х |
Рис. 26.8. Прохождение частицы через одномерный потенциальный барьер:
а и б – соответственно ступенчатый и симметричный прямоугольный потенциальный барьер
0, |
x < 0; |
0, x < 0 |
(область 1); |
|
|
, 0 ≤ x ≤ l |
|
||
U (x) = |
, x > 0, |
U (x) = U0 |
(область 2); |
|
U0 |
|
x > l |
(область 3). |
|
|
|
0, |
||
Пусть слева на границу барьера налетает частица (или поток частиц) с полной энергией Е (рис. 26.8, а). «Классическая» частица с энергией
E >U0 (E = E1) пройдет над барьером (R = 0), а при E <U0 (E = E2 ) отразится от него и будет двигаться в обратную сторону. В квантовой меха-
нике для микрочастицы при энергиях, превосходящих высоту барьера (и даже в отсутствие какого-либо барьера, например, при прохождении частицы над потенциальной ямой), есть вероятность надбарьерного отражения, когда частица отразится от барьера и будет двигаться в обратную сторону. Этот результат является чисто квантовым и объясняется наличием у частицы волновых свойств.
Вычислим вероятность надбарьерного отражения (рис. 26.8, а). В случае одномерного движения частицы слева направо вдоль оси Х уравнение Шрёдингера (26.15) запишется для областей 1 и 2 соответственно в виде (26.16):
d2ψ |
|
d2ψ |
2 |
|
|
|
1 |
+ k2 ψ = 0, |
|
+ η2 ψ |
|
= 0, |
|
d x2 |
d x2 |
|
||||
1 |
|
2 |
|
|||
где k = 2mE ; η = 2m(E −U0 )
; η = 2m(E −U0 ) . Общие решения будут следующими: ψ1(x) = A1eik x + B1e−ik x (при x < 0),
. Общие решения будут следующими: ψ1(x) = A1eik x + B1e−ik x (при x < 0),
ψ2(x) = A2eiη x (при x > 0),
где A1, B1 и A2 – постоянные. Решение уравнения Шрёдингера для области 1 является линейной комбинацией двух решений вида (26.16а). Пер-
95

вое слагаемое волновой функции ψ1(x) соответствует падающей на барьер частице, а второе слагаемое – отраженной от барьера частице. В области 2 частица, прошедшая над барьером, может двигаться только в положительном направлении оси Х.
Согласно условию непрерывности волновой функции на границе областей 1 и 2 запишем, что
ψ1 |
|
= ψ2 |
|
, |
dψ1 |
|
= |
dψ2 |
|
|
. |
|
|
||||||||||
|
|
d x |
|
d x |
|||||||
|
x=0 |
|
|
x=0 |
x=0 |
|
|
x=0 |
|||
|
|
|
|
|
|
|
|
||||
Тогда уравнения, связывающие постоянные A1 , B1 и A2 , имеют вид
A1 + B1 = A2 и ik A1 − ik B1 = iη A2.
Следовательно, |
|
|
|
||
B1 = |
k − η |
A2 = |
2k |
||
|
A1, |
|
A1. |
||
k + η |
k + η |
||||
Теперь получаем, что при движении над потенциальным барьером частица действительно с некоторой вероятностью R должна отражаться и менять направление движения. Согласно определению (26.29)
|
|
|
|
B1 |
|
|
2 |
|
E − |
E −U0 |
2 |
|
|
|
|
|
|
|
|
|
|||||||
R = |
|
|
|
|
|
= |
|
|
. |
(26.30) |
|||
|
|
|
|
|
2 |
E + |
E −U0 |
||||||
|
|
||||||||||||
|
|
|
|
A |
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Аналогично можно вычислить коэффициент пропускания D (D =1− R):
D = |
η |
|
|
A2 |
|
2 |
. |
(26.30а) |
|
|
|
|
|||||||
|
|
|
|
||||||
k |
|
A1 |
|
|
2 |
||||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
При движении частицы (или потока частиц) слева направо с энергией E <U0 коэффициент η будет мнимым и волновая функция экспоненциально затухает внутрь потенциального барьера (область x > 0), очень быстро становясь пренебрежимо малой. Отраженный поток равен падающему потоку частиц, т.е. частицы не могут проникнуть далеко и должны полностью отразиться от барьера с вероятностью R =1.
В классической физике проникновение частиц под барьер запрещено. Однако вероятность проникновения микрочастицы под барьер (область x > 0, рис. 26.8, а) отлична от нуля. Микрочастицу можно обнаружить
взапрещенной с точки зрения классической физики области, где E <U0,
вкоторой кинетическая энергия классической частицы p2 (2m) была бы отрицательна:
(2m) была бы отрицательна:
96

E = |
p2 |
+U (x), |
p2 |
|
|
|
< 0, |
||
2m |
2m |
|||
а ее импульс был бы мнимым.
Поясним прохождение микрочастицы в запрещенную область с помощью соотношения неопределенностей (26.2). Неопределенность импульса px микрочастицы, движущейся вдоль оси Х, на отрезке x = l составляет px ≥ 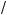 (2l). Тогда связанная с этим разбросом в значениях импульса кинетическая энергия ( px )2
(2l). Тогда связанная с этим разбросом в значениях импульса кинетическая энергия ( px )2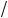 (2m) может оказаться достаточной для того,
(2m) может оказаться достаточной для того,
чтобы полная энергия частицы Е оказалась больше потенциальной U0 .
26.12. Туннельный эффект
Рассмотрим одномерный прямоугольный потенциальный барьер (рис. 26.9, а). Пусть слева (область 1) на него летит частица (или поток частиц). На языке квантовой теории будем рассматривать, как на барьер слева «падает» дебройлевская волна:
Ψ(x,t) = Aei(k x−ωt), |
(26.31) |
где k = 2mE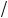 . Частота ω прошедших волн, так же как и отраженных, одна и та же (ω = E
. Частота ω прошедших волн, так же как и отраженных, одна и та же (ω = E ). Поэтому в дальнейших расчетах исследуем координатную часть этих волн ψ(x).
). Поэтому в дальнейших расчетах исследуем координатную часть этих волн ψ(x).
Будем решать стационарное уравнение Шрёдингера для свободной частицы (26.16). В табл. 26.1 представлен вид уравнения Шрёдингера и его решение для трех пространственных областей (рис. 26.9, а).
В случае, когда |
E >U0 , константа q опре- |
||
деляется |
так: |
q = 2m(E −U0 ) |
. Если |
E <U0, |
то q – мнимое число: q = iβ , где |
||
β = 2m(U0 − E) |
. Слагаемые, |
содержа- |
|
щие eikx и e−ikx, описывают волны, распространяющиеся соответственно в положительном и отрицательном направлениях оси Х. Результаты решения указанной задачи (рис. 26.9, б) внесем в табл. 26.1.
а
U
|
Е |
U0 |
|
|
|
|
1 |
2 |
|
|
3 |
б |
|
0 ψ |
(x) |
l |
Х |
ψ |
(x) |
2 |
|
ψ (x) |
|
|
|
|
|||
1 |
|
|
|
|
3 |
|
|
0 |
|
|
Х |
в |
|
|
|
|
ψ (x) 2 |
|
|
|
|
|
0Х
Рис. 26.9. К объяснению туннельного эффекта:
а – прямоугольный потенциальный барьер; б – закономерности изменения ψ-функции в областях 1, 2 и 3; в – график распределения плотности вероят-
ности ψ(x) 2местоположения частицы
97

|
|
|
|
|
|
|
|
|
|
Таблица 26.1 |
Вид решений стационарного уравнения Шрёдингера в случае одномерного |
||||||||||
|
|
|
|
|
|
|
|
прямоугольного потенциального барьера |
||
|
|
|
|
|
|
|
|
|
||
Область |
|
|
|
Уравнение |
Решение |
Решение |
||||
|
|
Шрёдингера |
при E >U0 |
при E <U0 |
||||||
|
|
|
||||||||
1 |
|
|
d2ψ1 |
|
+ k2ψ1 = 0 |
ψ1(x) = A1eikx + B1e−ikx |
ψ1(x) = A1eikx + B1e−ikx |
|||
x < 0 |
|
|
|
|
|
|
|
|||
|
|
d x |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
2 |
|
d2ψ |
|
|
|
|
||||
0 ≤ x ≤ l |
|
|
2 |
|
|
+q2ψ2 = 0 |
ψ2(x) = A2eiqx + B2e−iqx |
ψ2(x) = A2eβx + B2e−βx |
||
|
|
d x2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
||
|
d ψ3 |
+ k2ψ3 = 0 |
ψ3(x) = A3eikx |
ψ3(x) = A3eikx |
||||||
x > l |
|
|||||||||
|
2 |
|||||||||
|
|
|
dx |
|
|
|
|
|
|
|
Вид волновых функций, являющихся решениями уравнения Шрёдингера для областей 1, 2 и 3 (рис. 26.9, табл. 26.1) свидетельствует:
1) в области 1 волновая функция ψ1(x) представляет собой сумму двух плоских волн – падающей на барьер и отраженной от барьера. Падающая
волна характеризуется амплитудой A1 , а отраженная – амплитудой B1 ;
2) в области 2 при E >U0 имеются две плоские волны – падающая и отраженная от границы областей 2 и 3. При E <U0 функция ψ2(x) описывает состояние частицы, прошедшей в классически запрещенную область, и не соответствует плоским волнам, распространяющимся в обе стороны, так как показатели экспонент действительные. Можно показать, что при βl >>1 в случае высокого и широкого барьера B2 ≈ 0. Вероятность ψ(x) 2 убывает по экспоненте с глубиной проникновения частицы
взапрещенную область 2 вдоль оси Х;
3)в области 3 – области за барьером – имеется только плоская волна,
прошедшая через барьер с амплитудой А3 и распространяющаяся в положительном направлении оси Х.
На рис. 26.9, б показан качественный вид функций ψ(x) для случая
E <U0 , а также вид плотности вероятности ψ(x) 2 местоположения частицы: слева от барьера мы имеем падающую и отраженную волны, а за барьером – только прошедшую волну. Внутри барьера функция ψ(x) имеет неволновой характер и является неоднородной.
Условия непрерывности волновой функции ψ и ее производной ψ′x в точках x = 0 и x = l в случае, когда энергия частицы Е меньше U0 , дают следующую систему четырех уравнений для коэффициентов интегрирования:
98

ψ1(0) = ψ2 |
(0), или A1 + B1 = A2 + B2, |
|
|
|
|
|
||||||||
ψ2 |
(l) = ψ3(l), или A2e |
βl |
+ B2e |
−βl |
= A3e |
ikl |
, |
|
|
|
||||
|
|
|
|
|
|
(26.32) |
||||||||
ψ1′(0) = ψ′2 |
(0), или ik(A1 − B1) = β(B2 − A2 ), |
|
||||||||||||
|
|
|||||||||||||
ψ′ |
(l) = ψ′(l), или β(B e |
βl |
− A e |
−βl |
) = ikA e |
ikl |
|
|||||||
|
|
|
|
. |
|
|||||||||
2 |
3 |
|
2 |
|
|
2 |
|
|
|
|
3 |
|
|
|
В этой системе четырех уравнений имеется пять неизвестных. Однако если задать плотность потока частиц, падающих на барьер, то задача упрощается. Можно показать, что в случае однородного движения вдоль оси Х эта плотность задается соотношением
j = |
i |
(ψ |
dψ* |
− ψ* |
dψ |
|
|
|
|
), |
|||
2m |
d x |
|
||||
|
|
|
d x |
|||
в которое подставляется ψ = A1eikx . Таким образом, получают
jпад = |
|
A1 |
|
2 |
k |
|
|
|
|||||
|
|
|
|
. |
||
|
|
|
m |
|||
|
|
|||||
Аналогично для плотности потока отраженных частиц и частиц, прошедших через барьер, соответственно находим
jпрох = |
|
A3 |
2 |
k |
jотр = |
|
B1 |
|
2 |
k |
||
|
|
|
, |
|
|
|
|
. |
||||
|
|
m |
m |
|||||||||
|
|
|
|
|
||||||||
Обычно в подобных задачах плотность jпад выбирают такой, чтобы A1 =1. В этом случае система (26.32) будет неоднородной системой четырех линейных уравнений относительно четырех неизвестных коэффициентов. Решая систему, определяют A3 , а затем и прозрачность барьера согласно выражению (26.28):
|
|
|
|
|
|
|
|
|
A3 |
|
|
2 |
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
D = |
|
|
|
|
= |
A |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
A1 |
|
|
3 |
|
|
|||
При βl >>1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D ≈ D0 exp − |
|
|
|
|
2m(U |
0 − E) l , |
(26.33) |
|||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=16 |
E |
− |
E |
|
|
|
|
|
|
|
|
|
|
|||
где D0 |
|
1 |
|
|
– коэффициент, близкий к единице; т и Е – масса |
||||||||||||
|
|
|
|||||||||||||||
|
U0 |
|
|
U |
0 |
|
|
|
|
|
|
|
|
|
|
||
частицы и ее энергия. Как следует из выражения (26.33), чем шире барьер l, тем меньше вероятность прохождения сквозь него частицы.
99

U |
|
|
|
|
Если потенциальный барьер имеет сложную |
|||||
|
|
|
|
|
|
форму (рис. 26.10), то прозрачность барьера |
||||
E |
|
|
|
|
можно приближенно определить так: |
|
||||
|
|
|
|
|
2 x2 |
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
D ≈ D0 exp − |
|
∫ |
2m(U (x)− E) dx |
, (26.33а) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x1 |
x2 |
Х |
|
|
|||
|
|
|
|
1 |
|
|
||||
где D0 – постоянный множитель, зависящий от формы барьера; x1 и x2 – координаты начала и конца потенциального барьера U(x) для данного значения полной энергии Е частицы, т.е.
значения координат, при которых U (x) = E. Равенство (26.33а) является приближенным и тем точнее, чем меньше (U − E) по сравнению с Е.
Туннельный эффект играет заметную роль в тех случаях, когда прозрачность барьера D не слишком мала. С помощью формулы (26.33) можно оценить ширину потенциального барьера, для которого возможен туннельный эффект:
m(U0 − E) l ~1 или l ≤
~1 или l ≤  m(U0 − E) .
m(U0 − E) .
Следовательно, туннельный эффект возможен, когда линейные размеры потенциального барьера соизмеримы с атомными размерами. Напри-
D |
|
|
|
|
|
мер, при |
|
U0 − E =10 эВ |
для |
электрона |
||||
|
|
|
|
|
me ≈10 |
−30 |
кг, при l ≈10 |
−10 |
м коэффициент |
|||||
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
Квантовая частица |
прозрачности D ≈1 e . С увеличением мас- |
||||||||||
|
|
|
|
|
|
сы частицы и разности U0 − E |
прозрач- |
|||||||
|
|
|
«Классическая» |
ность барьера уменьшается. На рис. 26.11 |
||||||||||
|
|
|
приведена |
зависимость |
D(E U0 ) , рас- |
|||||||||
|
|
|
частица |
|||||||||||
|
|
|
|
|
|
считанная по формуле (26.33), – сплошная |
||||||||
0 |
1 |
2 |
E U0 |
|||||||||||
линия и зависимость |
D(E U0 ) для «клас- |
|||||||||||||
Рис. 26.11. Зависимость D от E U0 |
сической» частицы – пунктирная линия. |
|||||||||||||
Данные зависимости подчеркивают кван- |
||||||||||||||
|
|
|
частицы |
тово-механическую |
специфику микро- |
|||||||||
|
|
|
|
|
|
|||||||||
частиц.
Начальные представления о туннельном барьере были определены М.А. Леонтоновичем и Л.И. Мандельштамом в 1927 г. (проблема квантования для ангармоничного осциллятора). Теоретически эффект был предсказан в 1928 г. Г.А. Гамовым при объяснении альфа-распада в ядерной физике.
100
