Основные статистические показатели.
В психодиагностике часто используются различные цифры.
Переменные, представляющие собой результаты измерений, называются вариантами (они варьируются, то есть изменяются) и обозначаются Xi. Все значения переменной, расположенные в один ряд в порядке возрастания или убывания, образуют вариационный ряд. Количество повторений одинаковых результатов в составе вариационного ряда называется частотой данного значения переменной.
Данные вариационного ряда можно представить в форме таблицы.
Табличное представление значений варианты
№ п/п |
Варианта |
Частота |
1
|
Всегда |
6 |
2 |
Часто |
9 |
3 |
Иногда |
12 |
4 |
Довольно редко |
7 |
5 |
Никогда |
2 |
|
Итого |
36 |
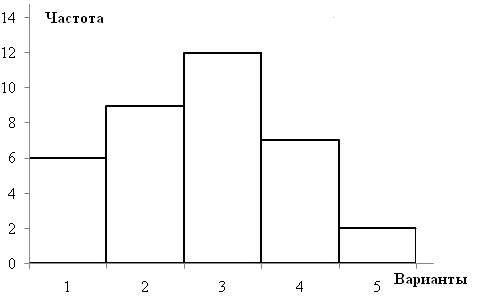
Рис. 5. Гистограмма частот различных значений варианты
Для дальнейшей статистической обработки необходимо вычислить среднее арифметическое, моду (или медиану), которые указывают на типичный, характеризующий данную группу или индивида результат.
Среднее арифметическое (среднее значение, или выборочное среднее) равно сумме всех значений варианты, деленной на количество членов вариационного ряда (N). Оно определяется по формуле 2:
,
(2)
или формуле 3
(3)
где Xi – варианта,
N – количество членов вариационного ряда.
Среднее значение используется в тех случаях, когда произведено интервальное измерение исследуемой переменной.
Медиана – это значение варианты, которое делит вариационный ряд пополам. Место расположения этого значения определяется по формуле 4
(4)
Мода – значение вариационного ряда, которое встречается наиболее часто.
Перечисленные три величины являются мерами центральной тенденции и используются в зависимости от характера распределения значений анализируемой переменной и задач, стоящих перед диагностом.
Для оценки изменения значений переменной используют такие характеристики, как дисперсия и среднее квадратичное (или стандартное) отклонение.
Дисперсия равна среднему квадрату отклонений значения варианты от среднего значения. Она выступает как одна из характеристик индивидуальных результатов разброса значений исследуемой переменной (например, оценок кандидата на вакантную должность) вокруг среднего значения.
Вычисление дисперсии осуществляется путем определения отклонения от среднего значения, квадрата указанного отклонения, сумы квадратов отклонения и среднего значения квадрата отклонения.
Стандартное отклонение широко применяется как мера разброса для различных характеристик.
Любое исследование, связанное с применением статистики и теории вероятностей, имеет целью изучение большого числа людей, их признакового пространства, для обобщений и типологических выводов относительно всей или определенной части наблюдаемой популяции. Эта популяция называется в психометрии генеральной совокупностью. В реальности исследователь не в состоянии изучить свойства всей популяции. Поэтому он работает с выборкой, то есть частью популяции, группой, а выводы с учетом определенных процессуальных правил распространяется на всю генеральную совокупность. Тем самым изучая свойства относительно небольшой группы, исследователь получает знание о свойствах генеральной совокупности в целом. По теореме Бернулли при бесконечном увеличении объема выборки эмпирическое распределение стремится по вероятности к распределению теоретическому.
Характеристики распределения генеральной совокупности называются параметрами, а характеристики выборочного распределения – оценками параметров. Для применения методов параметрической статистики осуществляется процедура определения вида статистического распределения эмпирических данных.
В психодиагностике в ходе оценки эмпирических данных используются различные распределения переменных. К наиболее известным относятся нормальное распределение, J-распределение, биноминальное распределение данных и др.
Метод наименьших квадратов в сочетании с гауссовским (нормальным) распределением эмпирических данных служат основой классической статистики. Предположения о нормальном распределении данных носят «модельный» характер. То есть реально они не могут выполняться абсолютно точно. Поэтому статистические выводы, составленные на основе модели, приближенной к нормальному распределению, носят более или менее точный характер. Оценка «приближенности» практической кривой к параметрам нормали осуществляется при помощи расчета: а) асимметрии и эксцесса и б) критериев согласия Пирсона (Хи-квадрат), Колмогорова и Ястремского. В первом случае оценивается положение вершины практической кривой относительно теоретической. Во втором – определение «участков» (групп частот) практической кривой относительно теоретической нормали.
То есть чем больше количество наблюдений, тем больше вероятность их совпадения и «более гладким» будет график распределения данных. Теоретически в условиях неопределенности результаты психологических переменных зависят от «случайности» и определяются большим количеством независимых факторов, влияние которых учесть невозможно. Но чем больше объем эмпирических данных, тем ближе реальное распределение к теоретически ожидаемой нормальной вероятности. График нормального распределения был впервые построен математиками П. Лапласом и К. Гауссом в результате исследований в области теории игр. В XIX веке бельгийский статистик А. Кутелет первым применил понятие нормального распределения эмпирических данных к исследованию антропометрических качеств человека. Он, в частности, заметив сходство графика нормального распределения с данными изменчивости антропометрических признаков, создал теорию, согласно которой стремление исследователей к экспериментальному «идеалу» или норме наталкивается в силу различных обстоятельств на неудачу. Опыт Кутелета по применению нормального распределения был переосмыслен и развит Ф. Гальтоном, который активно применял график нормального распределения для квантификации и преобразования данных индивидуальных и групповых различий.
Коэффициент асимметрии (As) показывает величину смещения вершины эмпирической кривой относительно расчетной вершины по горизонтали. Коэффициент эксцесса (Ex) определяет «крутизну» практической кривой, то есть смещение по вертикали.