1.4. Дифференциальные уравнения движения несвободной материальной точки в декартовой системе отсчёта

Р

Рис. 1.2

ассмотрим движение несвободной материальной точки под действием активных сил F_i^Е и реакций R_i^Е внешних связей в инерциальной системе отсчёта OXYZ (рис. 1.2).

Для обозначения инерциальной системы отсчёта использована аббревиатура ИСО.

Три уравнения: X = f₁(t); Y = f₂(t); Z = f₃(t) являются уравнениями движения точки в ИСО. Для рассматриваемой точки основное уравнение динамики имеет вид

m·a = P = ΣF_i^E + ΣR_i^E.

Спроецируем обе части последнего векторного равенства на координатные оси ИСО:

m· = Σ + Σ ;

m· = Σ + Σ ;

m· = Σ + Σ ,

где , , – проекции ускорения a на координатные оси; Σ , Σ , Σ – суммы проекций активных сил F_i^E на соответствующие координатные оси ИСО; Σ , Σ , Σ – суммы проекций реакций R_i^E внешних связей на оси ИСО.

Произведение массы m точки и проекции её ускорения a на координатную ось инерциальной системы отсчёта OXYZ равно сумме проекций активных сил F_i^Е и реакций R_i^Е внешних связей на ту же ось.

Последние уравнения называют дифференциальными уравнениями движения несвободной материальной точки в декартовой инерциальной системе отсчёта.

1.5. Дифференциальные уравнения движения несвободной материальной точки в естественных координатных осях

Естественные координатные оси – прямоугольная система осей с началом в движущейся точке, направленных соответственно по касательной, главной нормали и бинормали к траектории этой точки.

Из известного студентам курса кинематики уравнение движения точки в естественных координатных осях имеет вид S = f(t), где S – дуговая координата.

Рассмотрим движение несвободной материальной точки под действием активных сил F_i^E и реакций R_i^E внешних связей в естественных координатных осях (касательная, главная нормаль, бинормаль). Для понимания излагаемого материала напомним некоторые положения, относящиеся к этому движению.

Как это отмечалось ранее, естественными координатными осями называют три взаимно-перпендикулярные оси: касательная (единичный вектор τ всегда направлен в сторону возрастания дуговой координаты S); главная нормаль (единичный вектор n направлен к центру кривизны траектории движения); бинормаль (единичный вектор b перпендикулярен векторам τ и n и направлен так же, как и вектор k по отношению к векторам i, j в правой декартовой системе отсчёта OXYZ) (рис. 1.3).

Рис. 1.3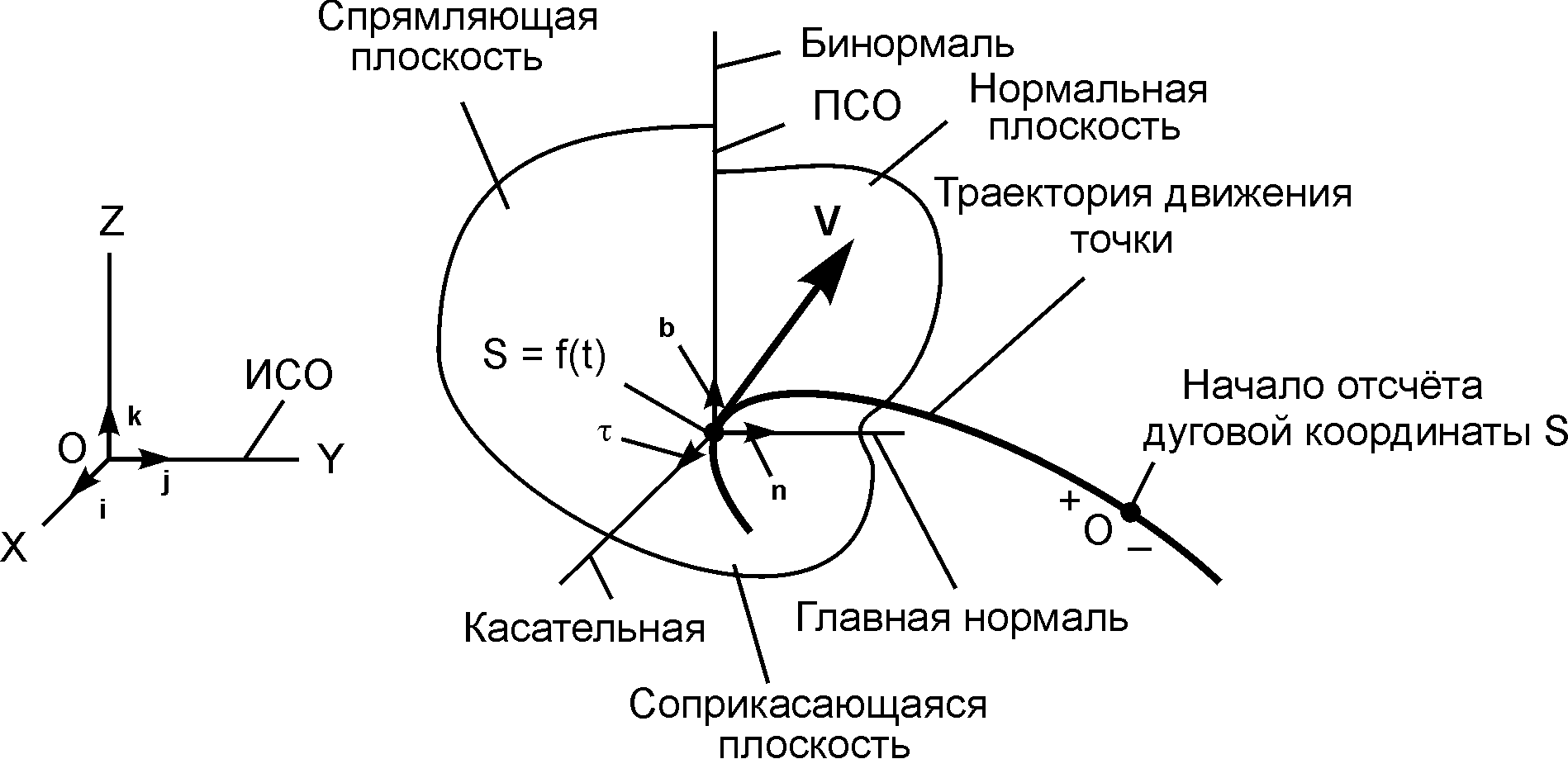

Начало естественных координатных осей всегда располагается на траектории в месте положения точки и, следовательно, перемещается вместе с точкой.

Таким образом, естественные координатные оси образуют подвижную систему отсчёта (ПСО).

Итак, рассматривается движение точки массой m в ПСО под действием активных сил и реакций внешних связей (рис. 1.4). Уравнение движения точки S = f(t) задано.

Из курса кинематики известно векторное выражение

a = a_oτ + a_on ,

где a – вектор ускорения точки; a_oτ – вектор касательного ускорения; a_on – вектор нормального ускорения.

Рис. 1.4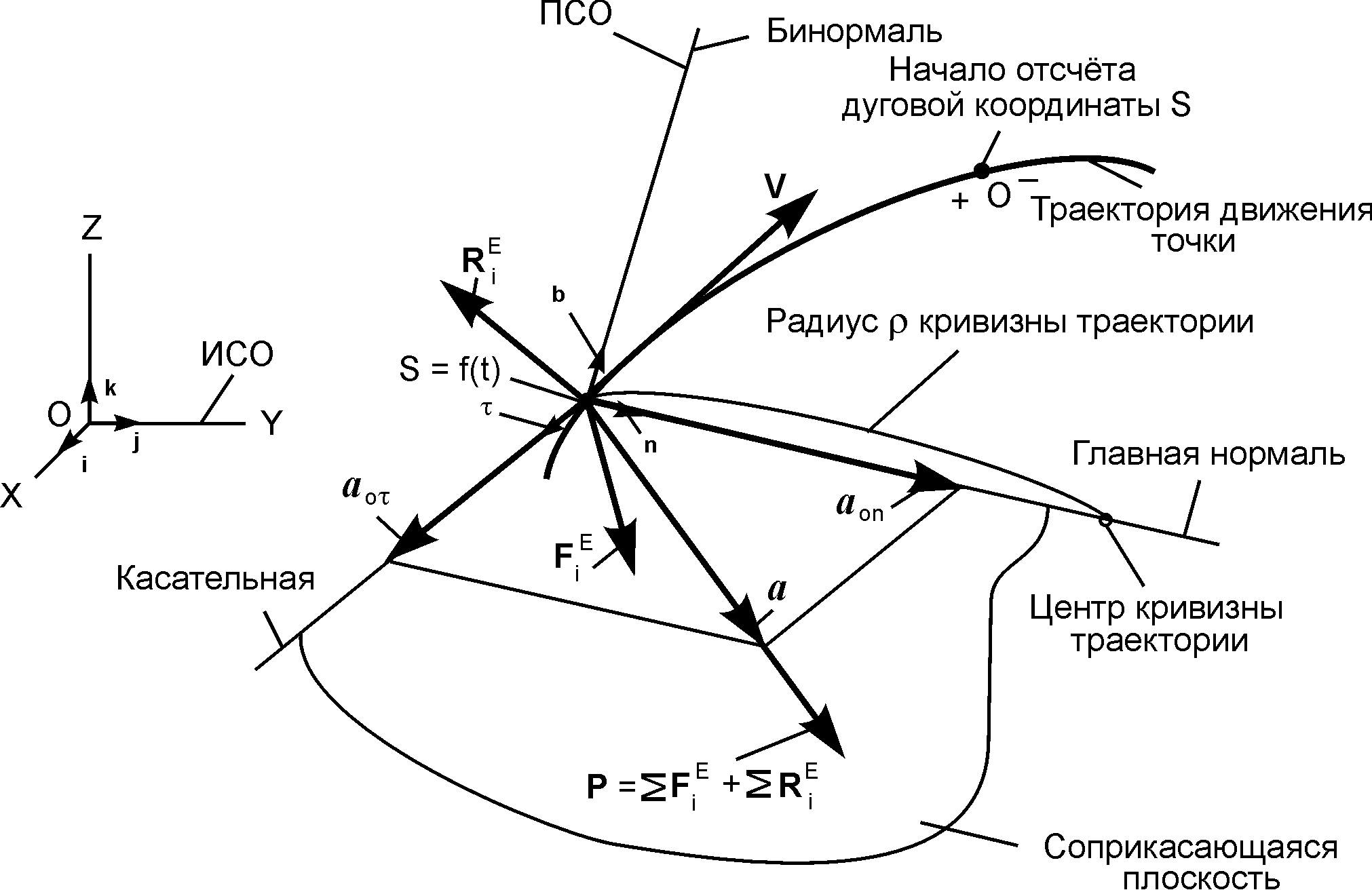

Спроецируем основное уравнение динамики m·a = ΣF_i^E + ΣR_i^E на координатные оси подвижной системы отсчёта:

m·a_oτ = Σ + Σ ;

m·a_on = Σ + Σ ;

m·a_ob = Σ + Σ ,

где a_oτ, a_on, a_ob – проекции ускорения a соответственно на касательную, главную нормаль и бинормаль; Σ , Σ , Σ – суммы проекций активных сил на оси ПСО; Σ , Σ , Σ – суммы проекций реакций внешних связей на оси ПСО.

Известно также, что a_oτ = ; a_on = /ρ, где ρ – радиус кривизны траектории точки. При этом a_ob = 0, так как вектор ускорения a лежит в соприкасающейся плоскости и на бинормаль не проецируется. С учетом изложенного выше последние математические выражения приобретают вид:

m· = Σ + Σ ;

m· /ρ = Σ + Σ ;

Σ + Σ = 0.

Произведения массы m точки и проекций её ускорения a на координатные оси ПСО равны сумме проекций активных сил F_i^Е и реакций R_i^Е внешних связей на те же оси ПСО.

Последние математические выражения называют дифференциальными уравнениями движения несвободной материальной точки в естественных координатных осях.

ПРИМЕЧАНИЕ. Дифференциальными уравнениями движения в естественных координатных осях удобно пользоваться тогда, когда точно известен вид траектории движения. В этом случае решение задачи существенно упрощается.