8.2. Удар шара о неподвижную плоскость

Рассмотрим удар поступательно движущегося шара о неподвижную плоскость (рис. 8.6).

Шар массой m движется поступательно и скорость V_C направлена по нормали к неподвижной массивной поверхности в точке А. В момент времени, когда шар достигает этой поверхности, происходит прямой центральный удар. Различают две фазы этого удара. В течение первой фазы шар деформируется до тех пор, пока скорость его не станет равной нулю. Во время этой фазы кинетическая энергия шара обращается в потенциальную энергию сил упругости деформируемых тел и частично расходуется на их нагревание. В течение второй фазы под действием сил упругости шар частично восстанавливает свою первоначальную форму. Из-за остаточных деформаций и нагревания шара первоначальная кинетическая энергия шара полностью не восстанавливается. Поэтому шар отделяется от неподвижной поверхности с абсолютной скоростью U_С, модуль которой меньше модуля его скорости V_C до удара.

Рис. 8.6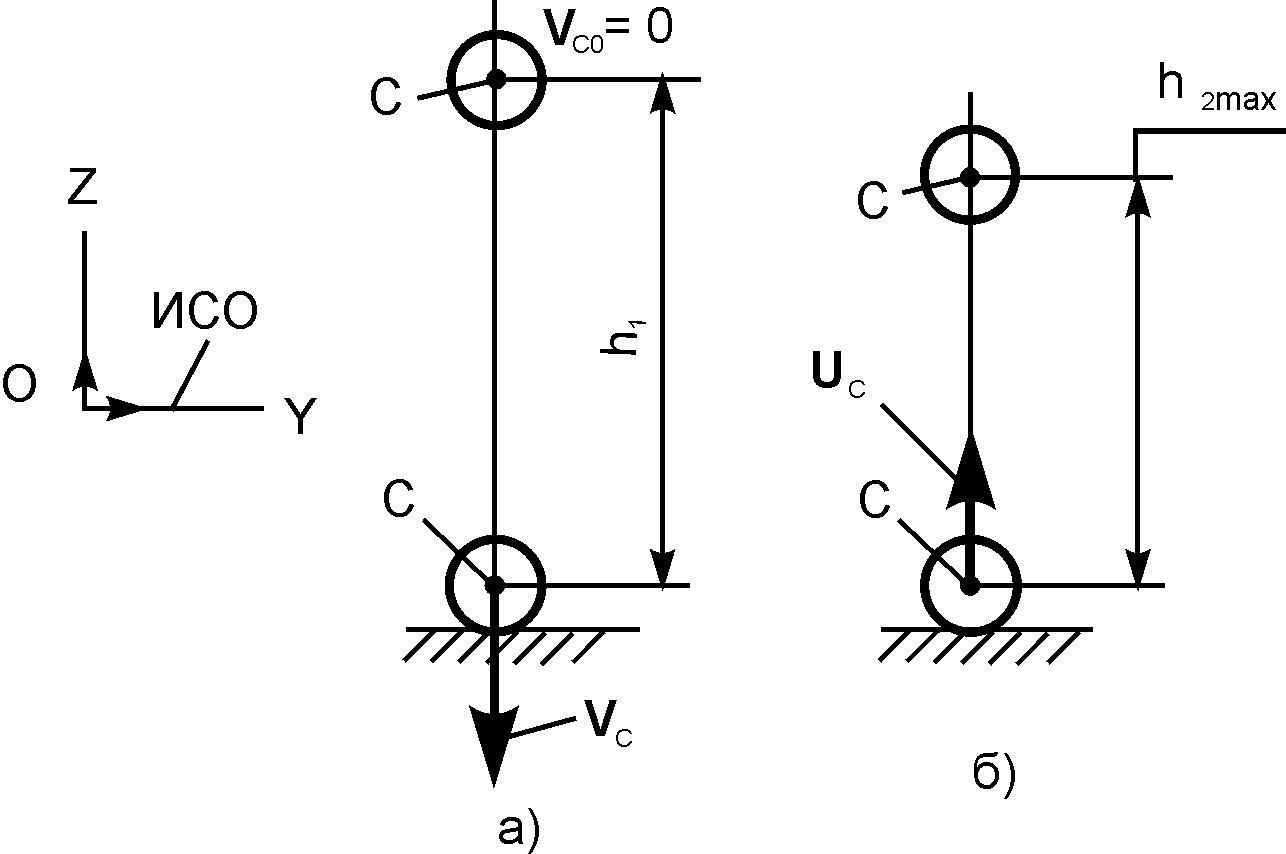

Согласно рис. 8.6, шар падает на неподвижную горизонтальную плоскость с высоты h₁, при этом начальная скорость его центра масс равна нулю (V_C0 = 0). В начале процесса удара скорость его центра масс равна V_C. В конце удара шар со скоростью центра масс U_С отрывается от неподвижной поверхности и поднимается на высоту h_2max, где скорость его центра масс равна нулю.

По известным величинам h₁, h_2max определяют коэффициент восстановления при ударе по формуле

k = .

Эта формула используется при экспериментальном определении коэффициента восстановления.

В случае абсолютно неупругого удара шар от плоскости не отделяется, т е. h₂ = 0. Тогда k = 0.

При абсолютно упругом ударе шар отскакивает от неподвижной плоскости и возвращается в исходное положение, т. е. h_2max = h₁. В этом случае k = 1.

При упругом ударе h_2max < h₁ и, следовательно, 0 < k < 1.

В случае прямого центрального удара тела о неподвижную поверхность модули скоростей связаны соотношением

U_С = k·V_C.

Р

Рис. 8.7

ассмотрим косой удар шара о неподвижную горизонтальную плоскость (рис. 8.7).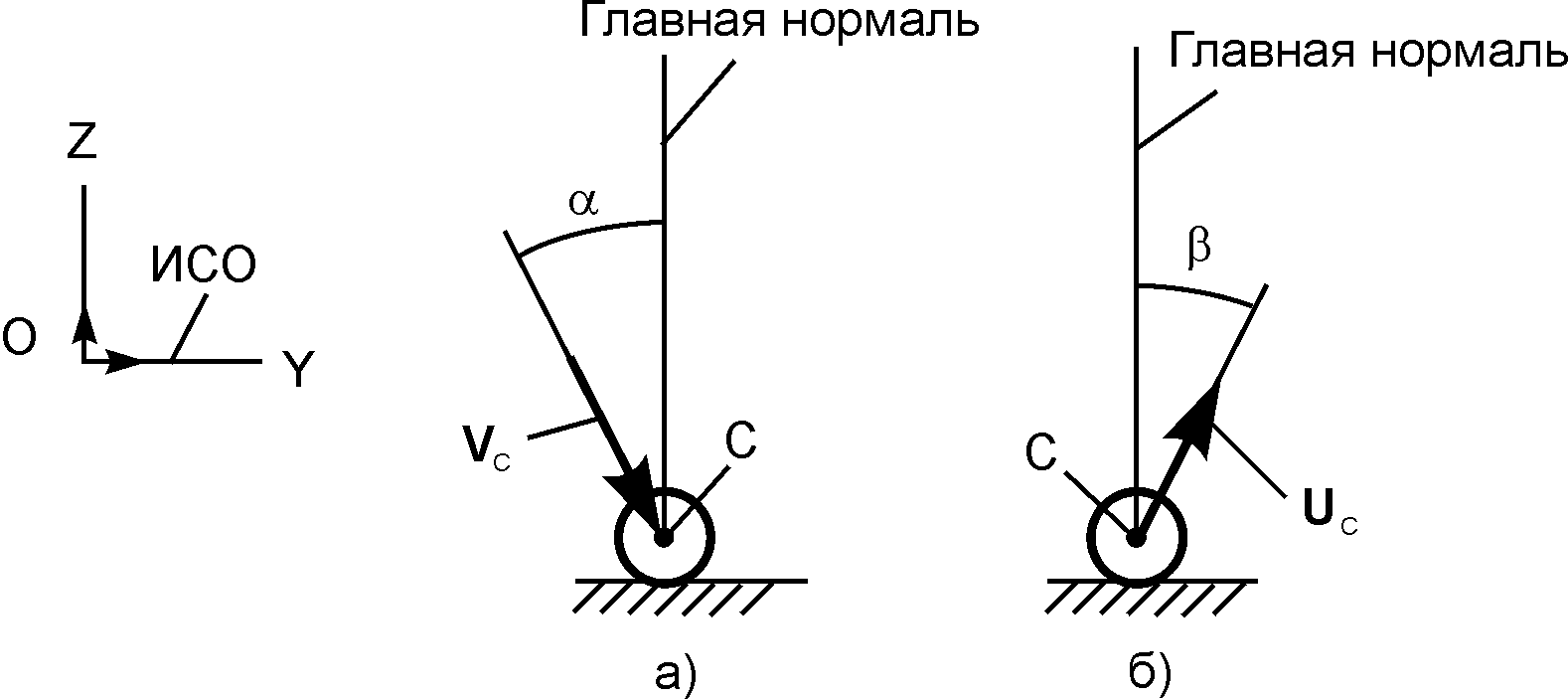

Шар ударяется о неподвижную плоскость со скоростью V_C, которая направлена к этой плоскости под углом α. После удара шар отскакивает от неподвижной плоскости со скоростью U_С, под углом β к плоскости. Коэффициент восстановления при ударе определяют по такой формуле

k = .

Последняя формула указывает удобный способ экспериментального определения коэффициента восстановления k при упругом ударе. По этому способу замеряют угол α и угол β отражения.

В случае абсолютно упругого удара угол α падения равен углу β отражения, откуда k = 1.

Задачи на определение коэффициента восстановления при ударе решают по следующему алгоритму.

1. Направить на рисунке главную нормаль (ось On) вдоль линии центров, а касательную (ось О – перпендикулярно к ней.

2. Вычислить проекции скоростей V_C1On, V_C2On центров С₁, С₂ масс соударяющихся тел в начале удара на главную нормаль.

3. Вычислить проекции скоростей U_C1On, U_C2On центров С₁, С₂ масс соударяющихся тел в конце удара на главную нормаль.

4. Определить коэффициент восстановления при ударе по формуле k = .