6.3. Принцип возможных перемещений
При решении задач на равновесие механических систем, например, для составной конструкции применяются соответствующие уравнения равновесия. Как правило, такие задачи являются статически неопределимыми. Для их решения требуется рассматривать равновесие каждого из тел системы под действием активных сил, реакций внешних связей и реакций внутренних связей. В результате того, что для каждого из тел системы составляются уравнения равновесия, приходится решать большие системы уравнений. Такой подход к решению задачи становится громоздким и потому малопригодным. В этих случаях целесообразно использовать принцип возможных перемещений, который существенно облегчает решение поставленной задачи.
Формулировка принципа возможных перемещений.
Для равновесия механической системы, на которую наложены стационарные идеальные связи, необходимо и достаточно, чтобы сумма работ активных (задаваемых) сил на любых возможных перемещениях механической системы равнялась нулю.
Этот принцип выражается формулой
δA = ΣδA(Fi) = ΣFi·δSi = ΣFi·δSi·cos(Fi, δSi) = 0,
где Fi – активная сила, приложенная к i-й точке механической системы; δSi – возможное перемещение точки приложения силы Fi.
Принцип возможных перемещений в декартовой системе отсчёта имеет вид
Σ(FiOX·δSiOX + FiOY·δSiOY + FiOZ·δSiOZ) = 0,
где FiOX, FiOY, FiOZ – проекции задаваемых (активных) сил на координатные оси; δSiOX, δSiOY, δSiOZ – проекции возможных перемещений δSi точки приложения сил Fi на координатные оси.
Если предыдущую формулу (ΣFi·δSi = ΣFi·δSi·cos(Fi, δSi) = 0) продифференцировать по времени, то получим
ΣFi·Vi = ΣFi·Vi·cos(Fi, Vi) = 0,
где Vi = d(δSi)/dt – возможная скорость точки приложения силы Fi.
Так как по определению F·V = F·V·cos(F, V) = N, где N – мощность, то последнее равенство трактуют как принцип возможных скоростей или принцип возможных мощностей.
Для равновесия механической системы, на которую наложены стационарные идеальные связи, необходимо и достаточно, чтобы сумма мощностей активных сил на любых возможных скоростях точек этой системы равнялась нулю.
Для закрепления изложенного теоретического материала рекомендуется выполнить курсовые задания Д 6, Д7.
6.3.1. Варианты курсового задания д 6
«Применение принципа возможных перемещений
к решению задач о равновесии сил, приложенных
к механической системе с одной степенью свободы»
Схемы механизмов, находящихся под действием взаимно уравновешивающихся сил, и необходимые для расчёта данные приведены в табл. 5.4. В расчётах использовать следующие условные обозначения: с – коэффициент жёсткости пружины (Н/см); h – деформация пружины (см); Q, P – силы (Н); М – момент пары сил (Н·м).
Примечания:
Вариант 6. Вес рукоятки О1А не учитывать.
Вариант 7. Пружина сжата.
Вариант 8. Пружина сжата.
Вариант 10. Вес рукоятки ОА не учитывать.
Вариант 14. Вес стержней ОА и ОВ не учитывать; пружина растянута.
Вариант 16. Вес стержней О1А и О2В не учитывать.
Вариант 18. Р – вес блока радиуса R3.
Вариант 19. Вес звена АВ не учитывать.
Вариант 24. Пружина сжата.
Вариант 25. Вес стержней АО и ВО не учитывать. Пружина растянута.
Вариант 26. Пружина растянута.
Применяя принцип возможных перемещений и пренебрегая силами сопротивления, определить величину, указанную в последнем столбце табл. 5.4.
Таблица 5.4
Номер варианта |
Расчётная схема механизма |
Исходные данные, определяемая величина |
1 |
2 |
3 |
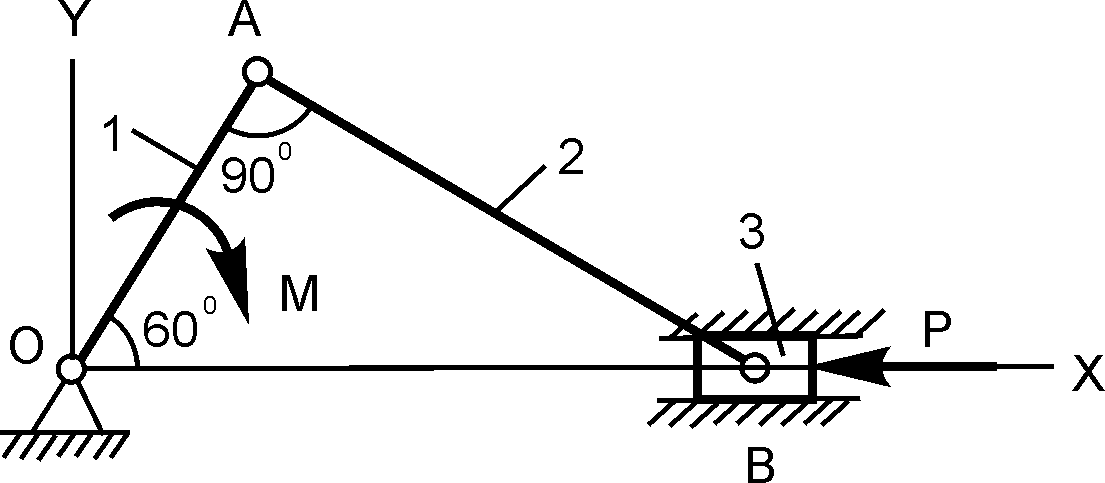
1 |
|
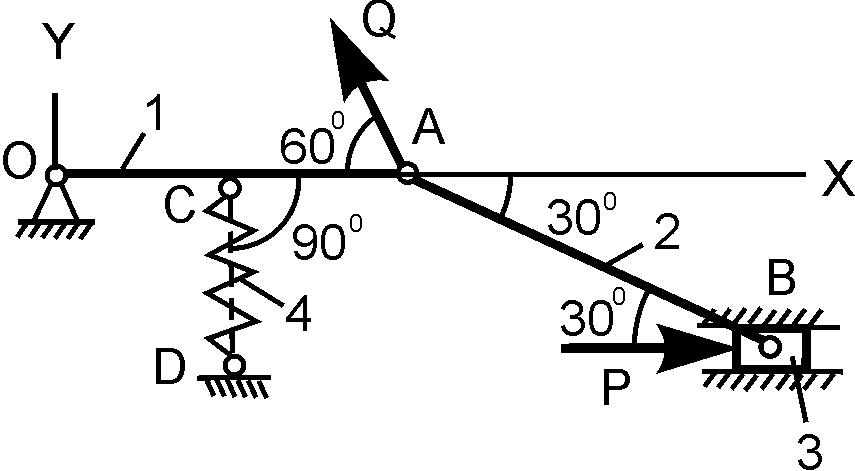
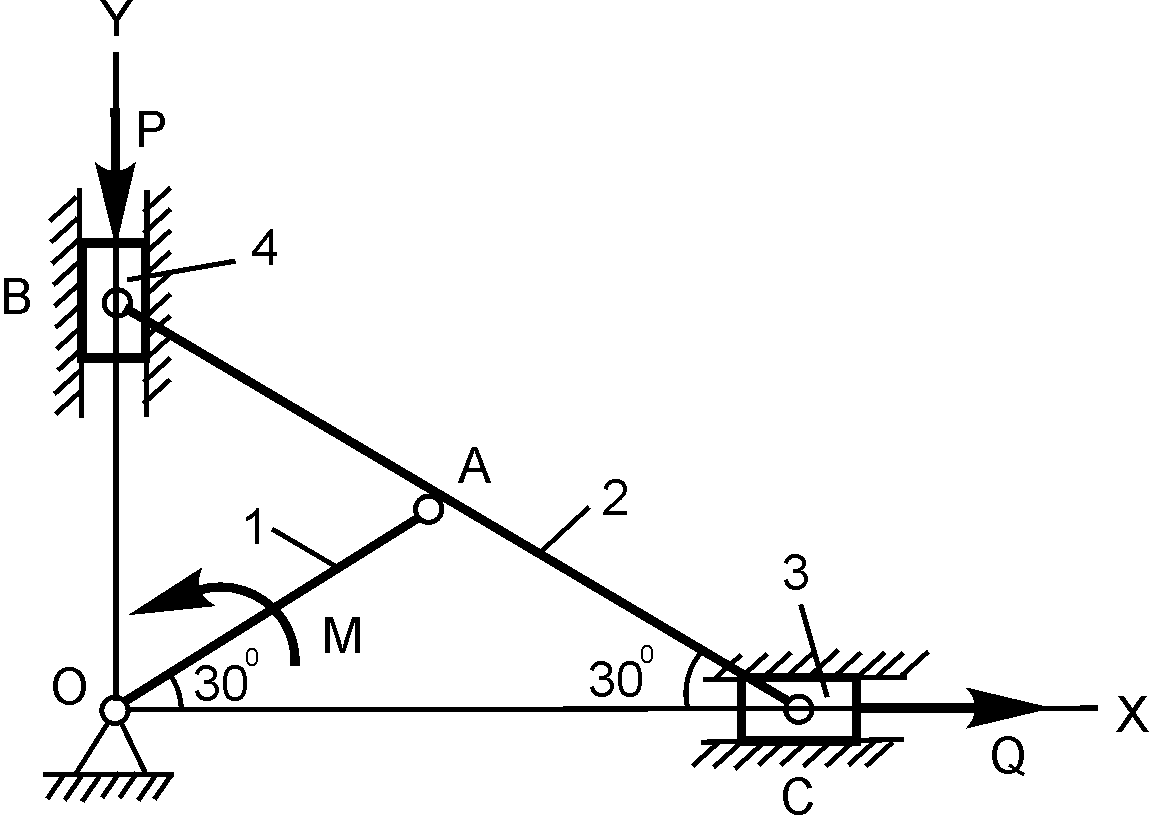
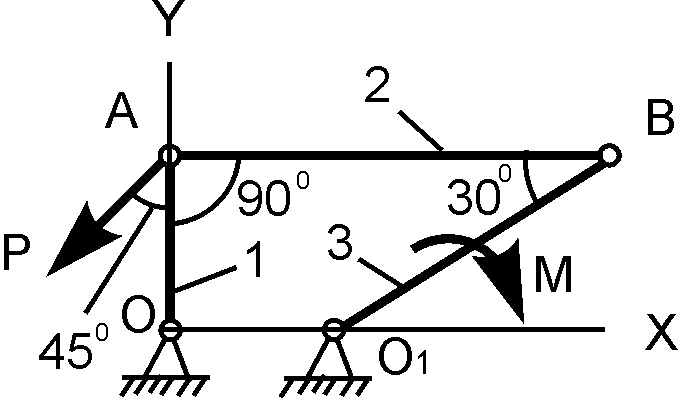
ОА = 10 см; М = 20 Н·м; P = ? |
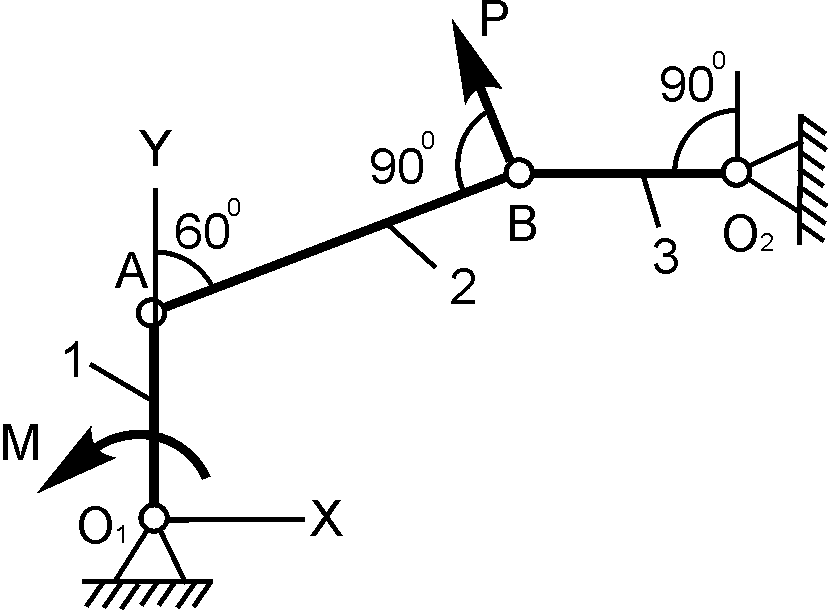
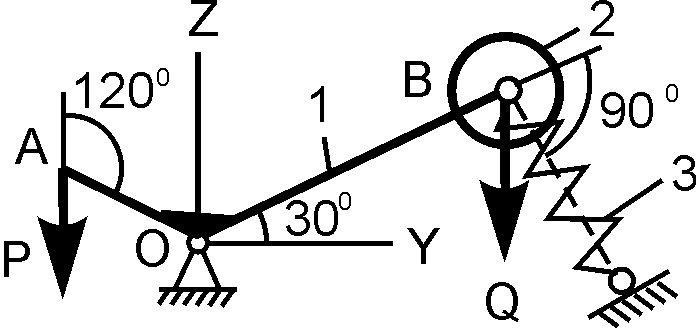
2 |
|
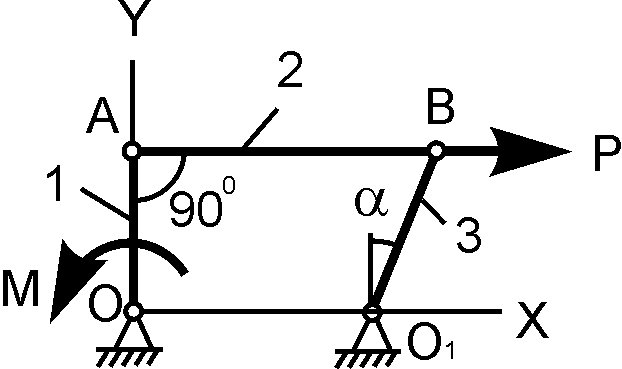
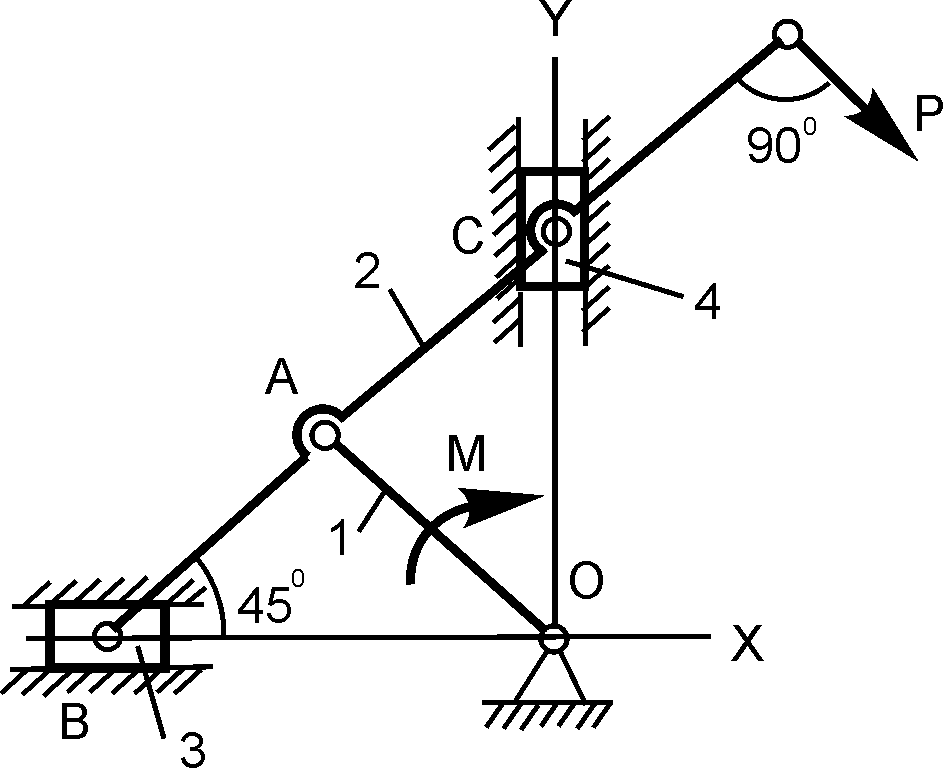
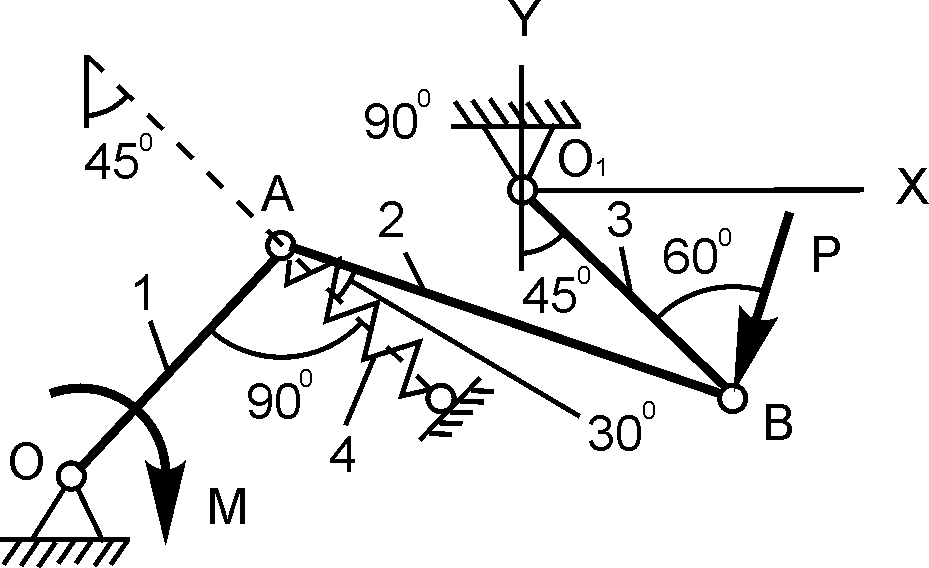
О1А = 20 см; Р = 100 Н; M = ? |
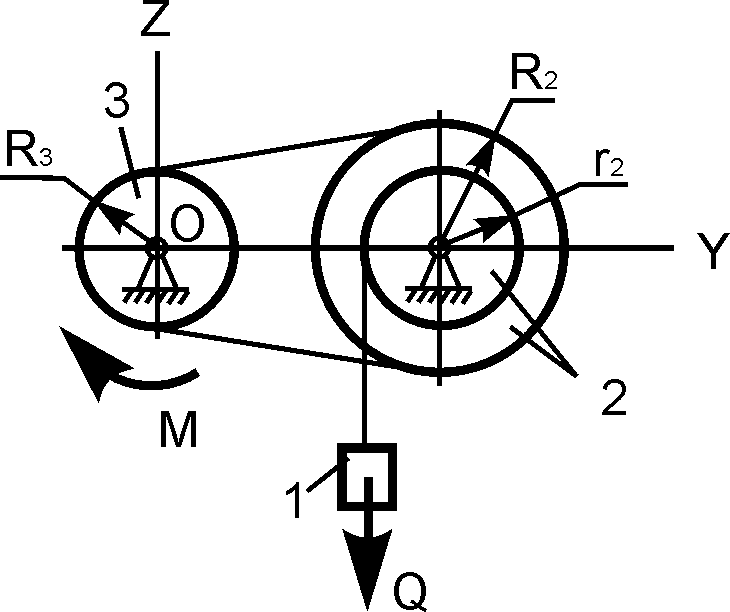
3 |
|
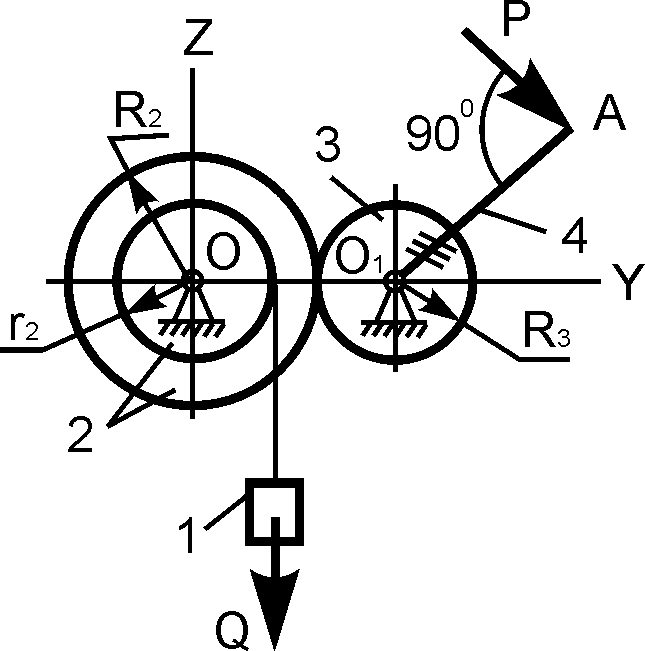
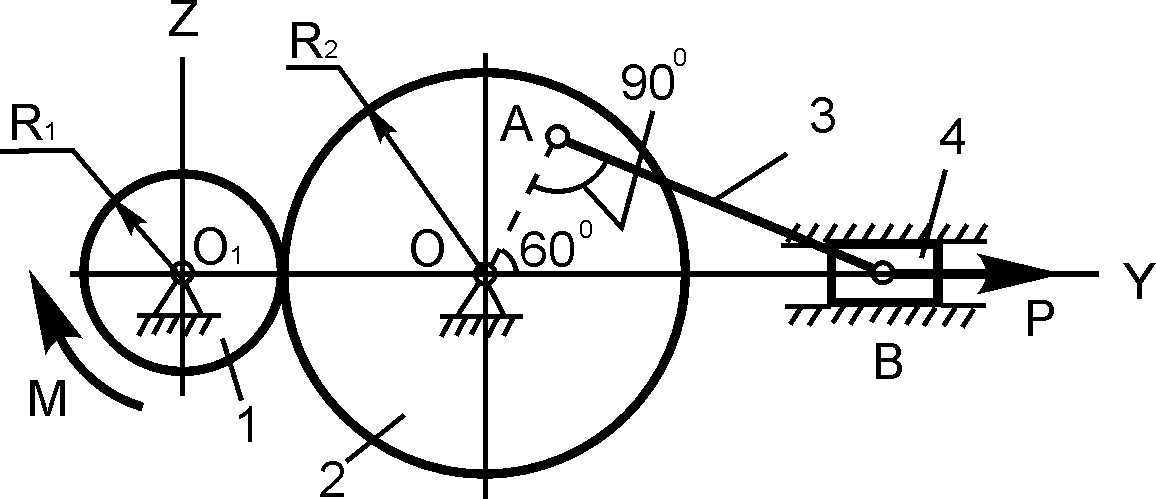
R2 = 40 см; r2 = 30 см; R3 = 20 см; M = 100 Н·м; Q = ? |
Продолжение табл. 5.4
1 |
2 |
3 |
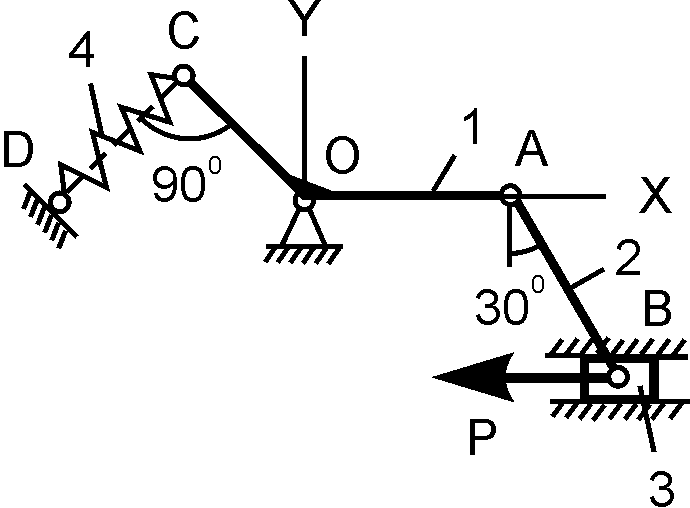
4 |
|
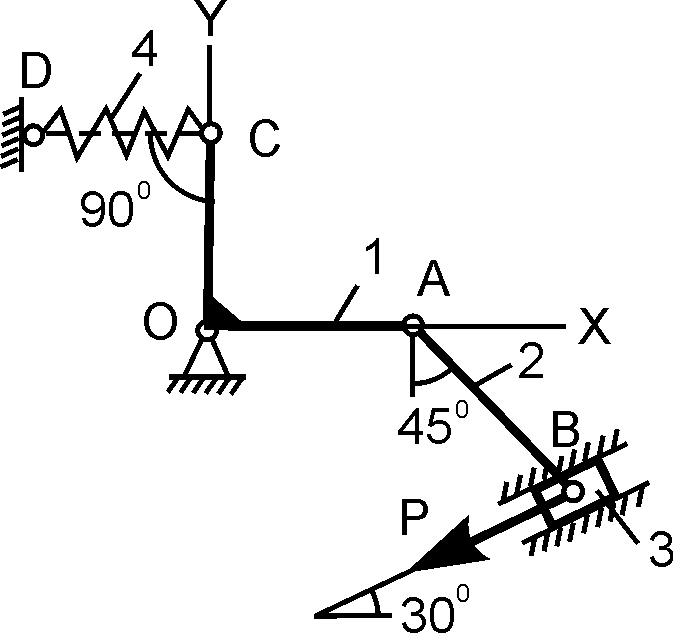
ОС/ОА = 4/5; Р = 200 Н; h = 4 см; с = ? |
5 |
|
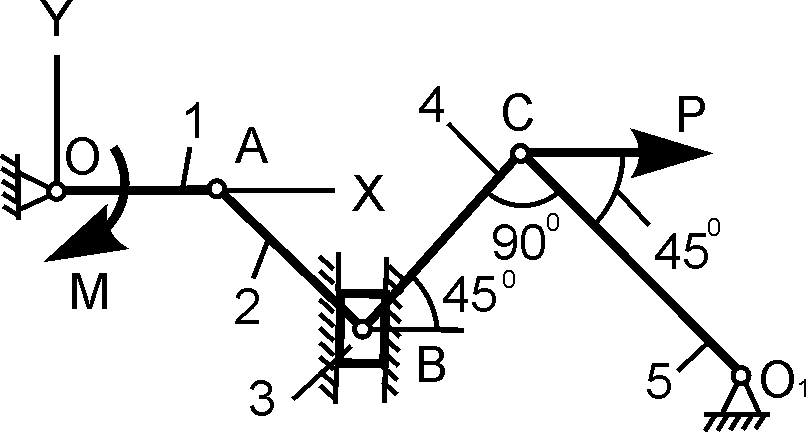
ОА = 100 см; М = 10 Н·м; P = ? |
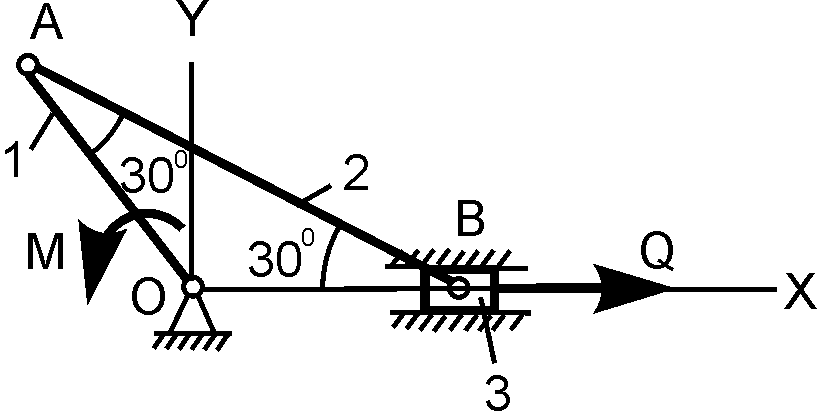
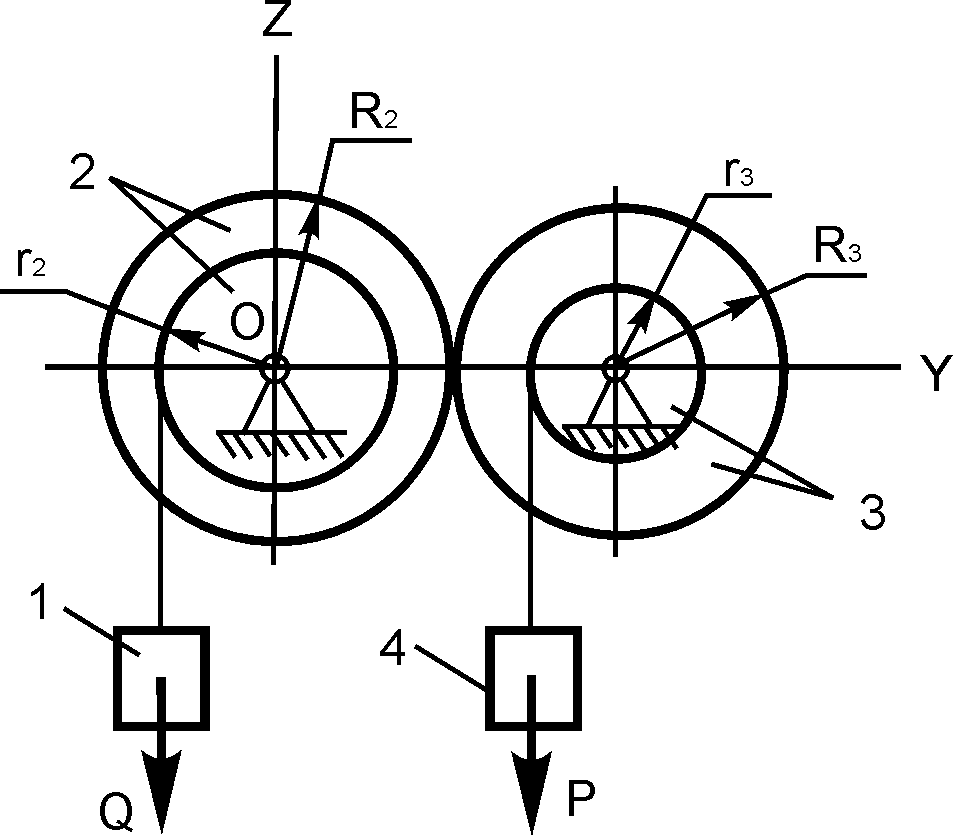
6 |
|
R2 = 50 см; r2 = 15 см; R3 = 20 см; О1А = 80 см; Q = 200 H; P = ? |
Продолжение табл. 5.4
1 |
2 |
3 |
7 |
|
OC = OA; с = 10 Н/см; h = 3 см; P = ? |
8 |
|
ОС = АС; Р = 200 Н; с = 10 Н/см; h = 2 см; Q = ?
|
9 |
|
ОА = 20 см; Q = 200 H; M = ? |
Продолжение табл. 5.4
1 |
2 |
3 |
10 |
|
R2 = 40 см; r2 = 15 см; R3 = 20 см; ОА = 100 см; Q = 2000 H; h = 4 см; с = ? |
11 |
|
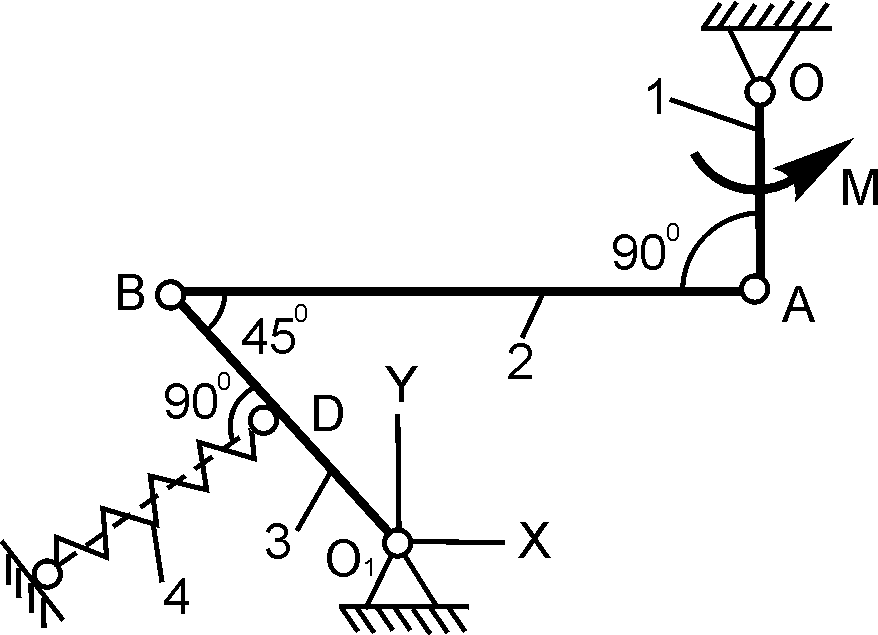
ОА = 20 см; М = 300 Н·м; P = ? |
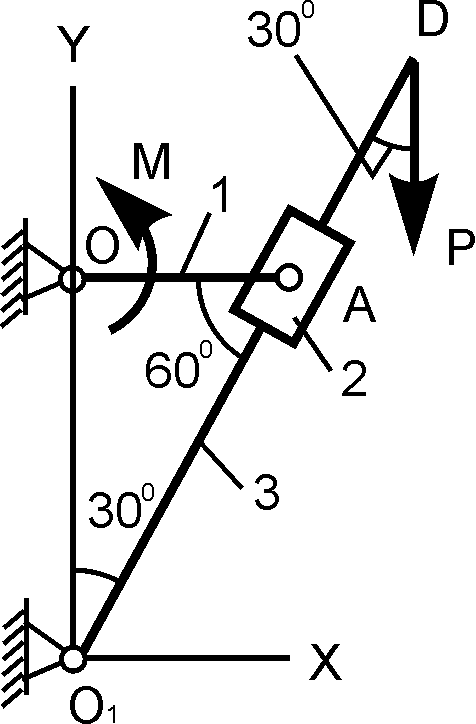
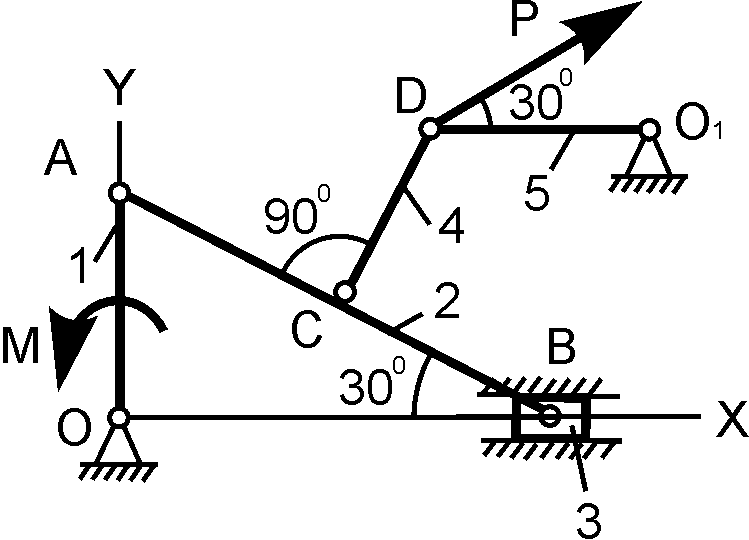
12 |
|
O1D = 60 см; АО = 20 см; М = 100 Н·м; P = ? |
Продолжение табл. 5.4
1 |
2 |
3 |
13 |
|
ОА = 40 см; М = 200 Н·м; P =? |
14 |
|
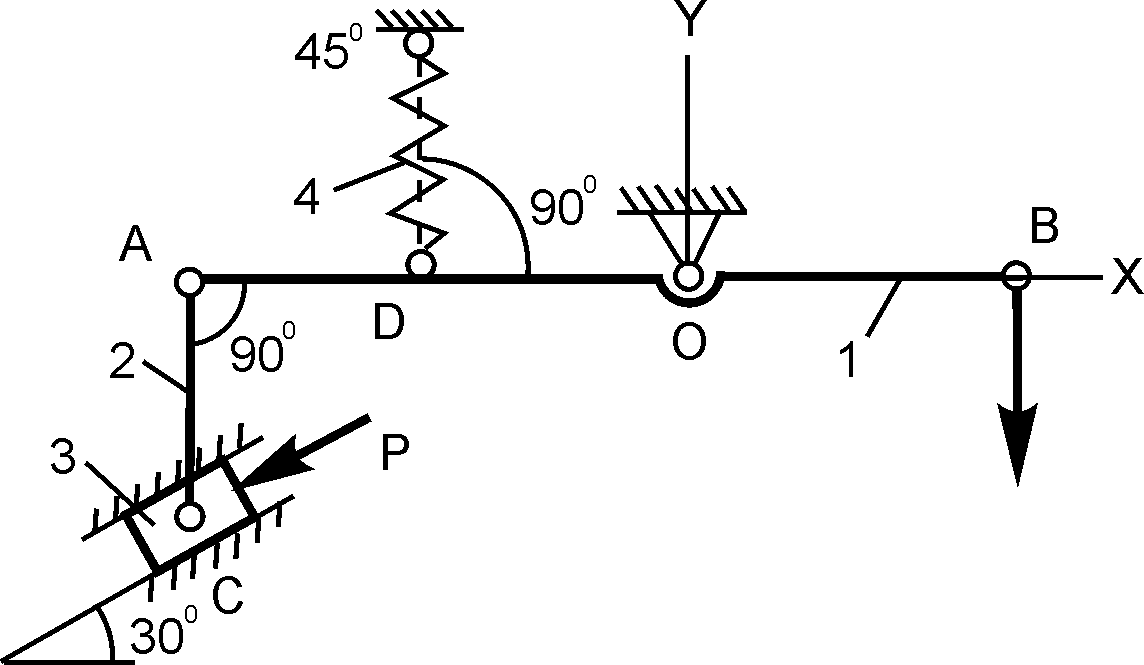
ОВ = 2ОА; Q = 20 H; с = 25 Н/см; h = 3 см; P = ? |
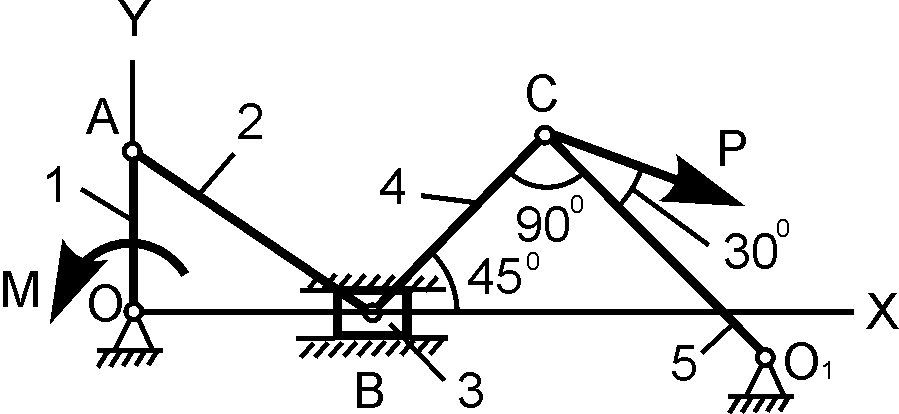
15 |
|
АС = ОС = ОD; Q = 3000 H; с = 250 Н/см; h = 3 см; P = ? |
Продолжение табл. 5.4
1 |
2 |
3 |
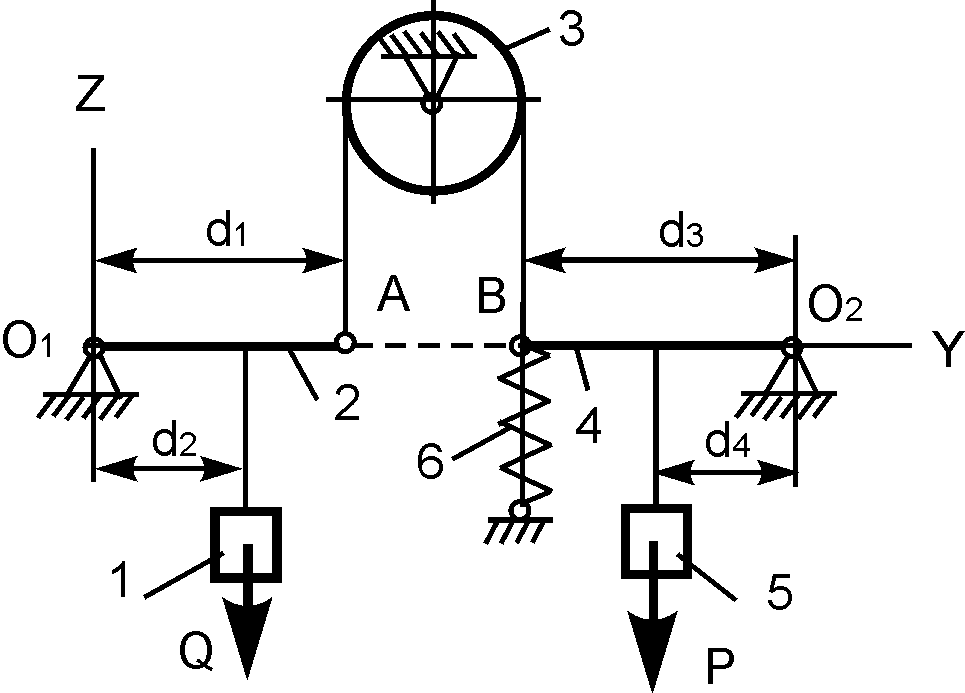
16 |
|
d1 = 100 см; d2 = 60 см; d3 = 80 см; d4 = 40 см; Q = 5000 H; c = 100 Н/см; h = 4 см; P = ? |
17 |
|
ОА = 20 см; М = 200 Н·м; P = ? |
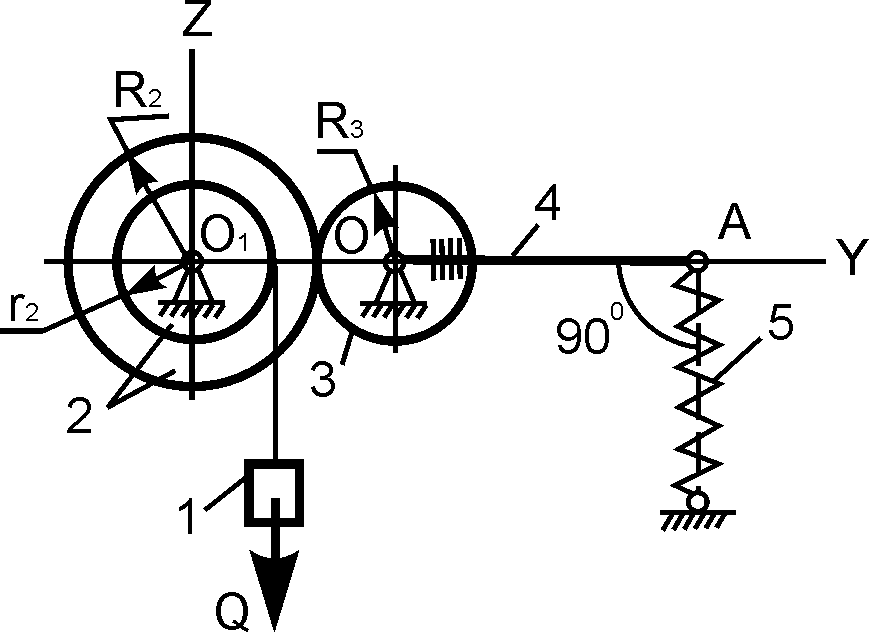
18 |
|
Q = 200 H; P = 200 H; с = 100 H/см; h = ? |
Продолжение табл. 5.4
1 |
2 |
3 |
19 |
|
R1 = 20 см; R2 = 30 см; ОА = 25 см; М = 100 Н·м; P = ? |
20 |
|
ОА=АВ =50 см; АС = 50 см; Q = 50 H; P = 100 H; M = ? |
21 |
|
ОА=АВ= 25 см; АС=DC= 25 см; Р = 200 Н; M = ? |
Продолжение табл. 5.4
1 |
2 |
3 |
22 |
|
ОА = 40 см; М = 400 Н/см; P = ? |
23 |
|
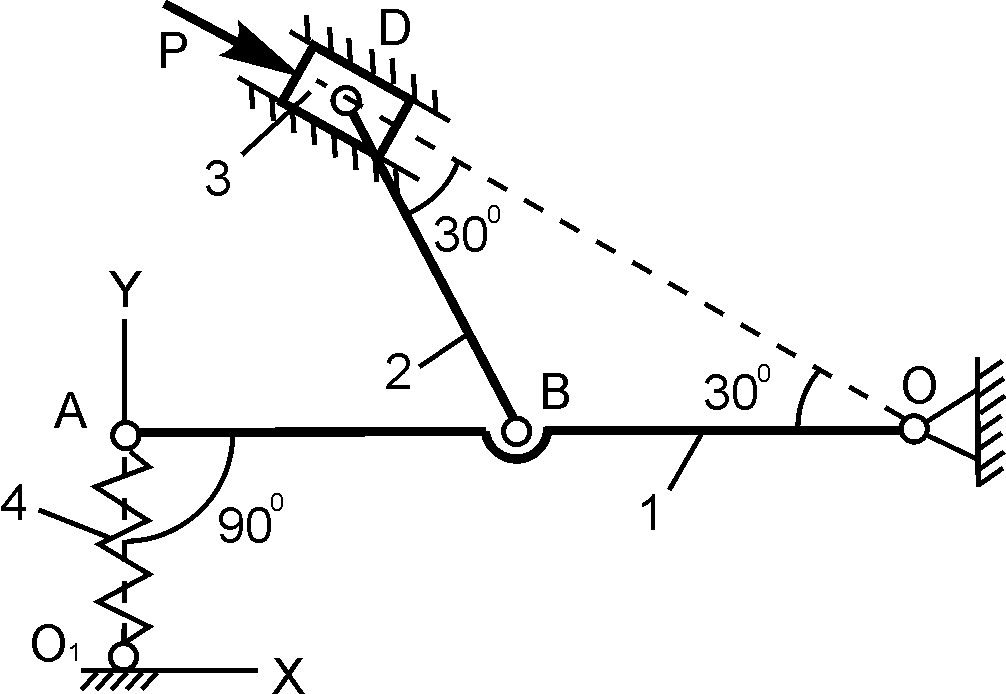
ОС =2ОА = 1 м; Р = 200 Н; М = 50 Н·м; с = 50 Н/см; h = ? |
24 |
Q
|
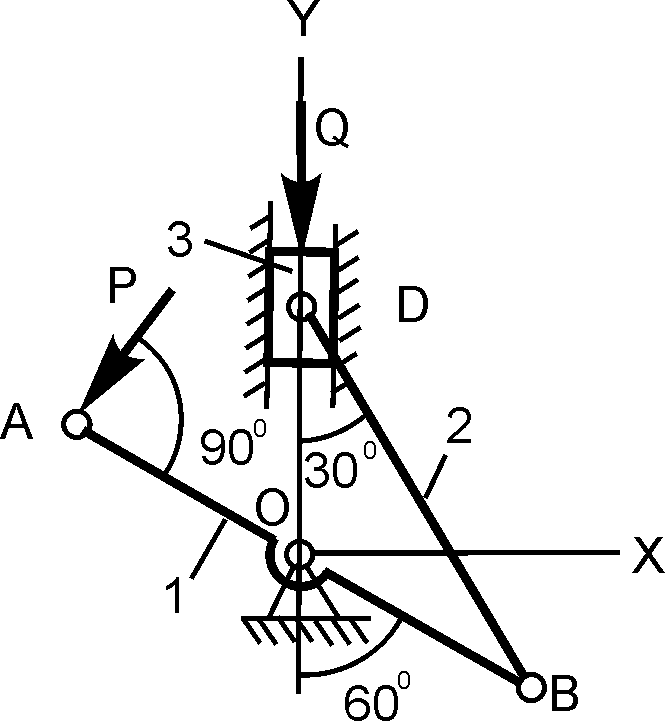
AD = OD = OB; P = 250 H; c = 150 H/см; h = 2,5 см; Q = ? |
Продолжение табл. 5.4
1 |
2 |
3 |
25 |
|
OD=DB=0,8AO; Q = 400 H; c = 120 H/см; h = 3 см; P = ? |
26 |
|
ОА = 25 см; Р = 500 Н; М = 120 Н·м; h = 2 см; с = ? |
27 |
|
ОВ = АВ; c = 180 Н/см; h = 2 см; P = ? |
Окончание табл. 5.3
1 |
2 |
3 |
28 |
|
ОВ = (5/4)ОА; Р = 450 Н; Q = ? |
29 |
|
AO = 30 см; BD = O1D; M = 120 H·м; с = 100 Н/см; h = ? |
30 |
|
R2 = 36 см; r2 = 15 см; R3 = 20 см; r3 = 10 см; Р = 600 Н; Q =? |
