5.6.3. Приведение сил инерции точек твёрдого

тела к простейшему виду

В данном учебно-методическом пособии рассматриваются неизменяемые механические системы, в которые входят тела, осуществляющие следующие виды движений: поступательное, вращательное, плоскопараллельное.

При поступательном движении силы инерции материальных точек приводятся к главному вектору Ф^* сил инерции, который прикладывается в центре масс твёрдого тела (рис. 5.37) и определяется по формуле

Ф

Рис. 5.37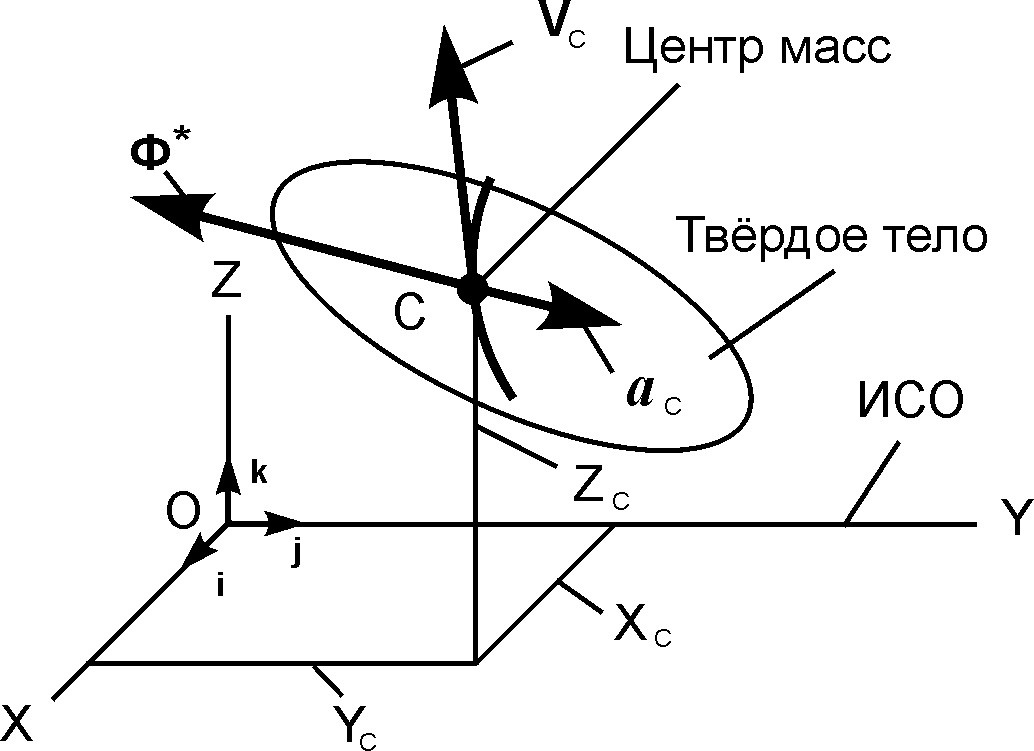

^* = – m·a_С.

Согласно рис. 5.37 главный вектор сил инерции Ф^* направлен в сторону, противоположную ускорению a_С. Модуль главного вектора сил инерции определяется по формуле Ф^* = m·a_С.

Р

Рис. 5.38

ассмотрим вращательное движение твёрдого тела относительно оси ОХ, которая не проходит через его центр масс (рис. 5.38).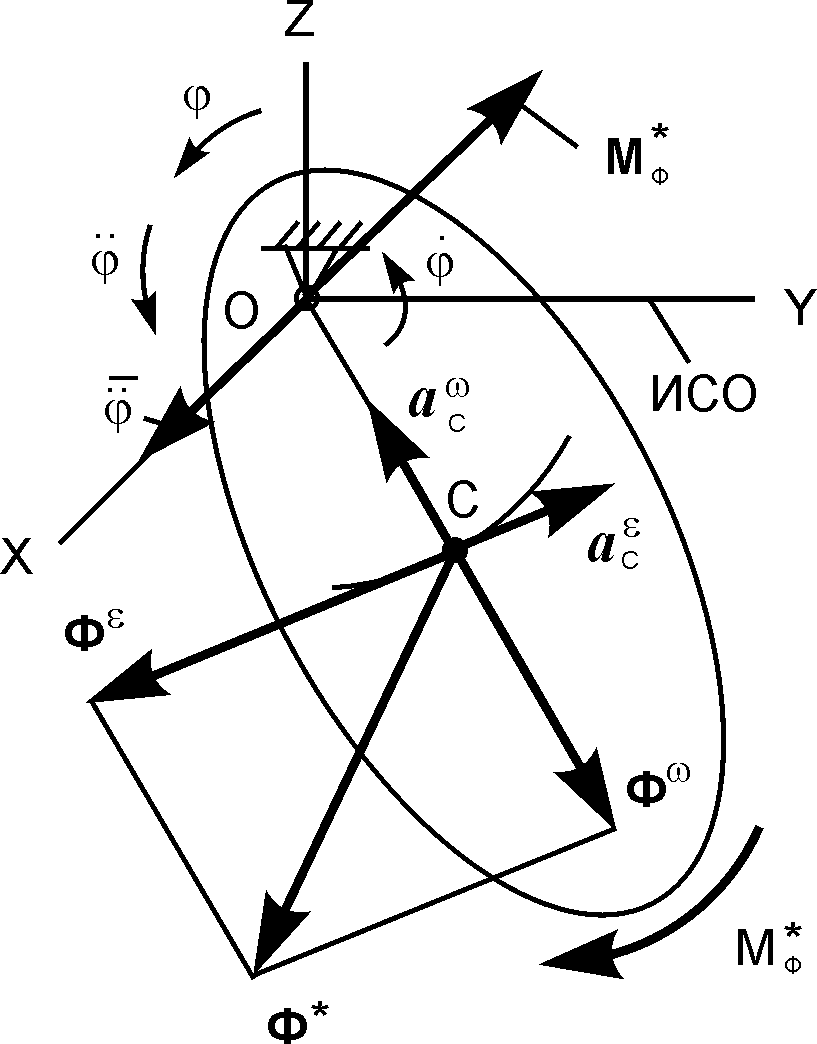

Согласно положениям кинематики имеем векторное равенство

a_С = + ,

где a_С – ускорение центра масс; – центростремительное ускорение центра масс; – вращательное ускорение центра масс.

В рассматриваемом случае силы инерции материальных точек тела приводятся к главному вектору Ф^* сил инерции и главному векторному моменту , определяемым по формулам:

Ф^* = Ф^ω + Ф^ε;

= – J_CX1· ,

где Ф^ω = – m· – центробежная сила инерции; Ф^ε = – m· – вращательная сила инерции; J_CX1 – момент инерции тела относительно оси СХ₁, проходящей через центр масс; – вектор углового ускорения.

Направления сил инерции Ф^ω, Ф^ε показаны на рис. 5.36. Модули составляющих Ф^ω, Ф^ε главного вектора Ф^* сил инерции и приведённого момента сил инерции определяют по формулам:

Ф^ω = m·(( )·CO); Ф^ε = m·(I I·CO); = М^Φ = J_CX1·I I,

где m, , I I – соответственно масса, угловая скорость и модуль углового ускорения тела; СО – расстояние от центра масс до оси вращения.

В инженерной практике наиболее часто используется вариант, в котором центробежная и вращательная силы инерции прикладываются в центре масс (см. рис. 5.38). Этот вариант и рекомендуется для дальнейшего использования как основной вариант.

Для общего ознакомления приведём и другие варианты приложения сил инерции.

Рассмотрим вариант вращательного движения твёрдого тела, при котором силы инерции Ф^ω, Ф^ε прикладываются на оси вращения (рис. 5.39).

В этом случае модули искомых инерционных нагрузок определяются по формулам:

Ф^ω = m·( ·CO); Ф^ε = m·(I I·CO); = М^Φ = J_ОX·I I,

где J_ОХ – момент инерции тела относительно оси вращения.

Рис. 5.39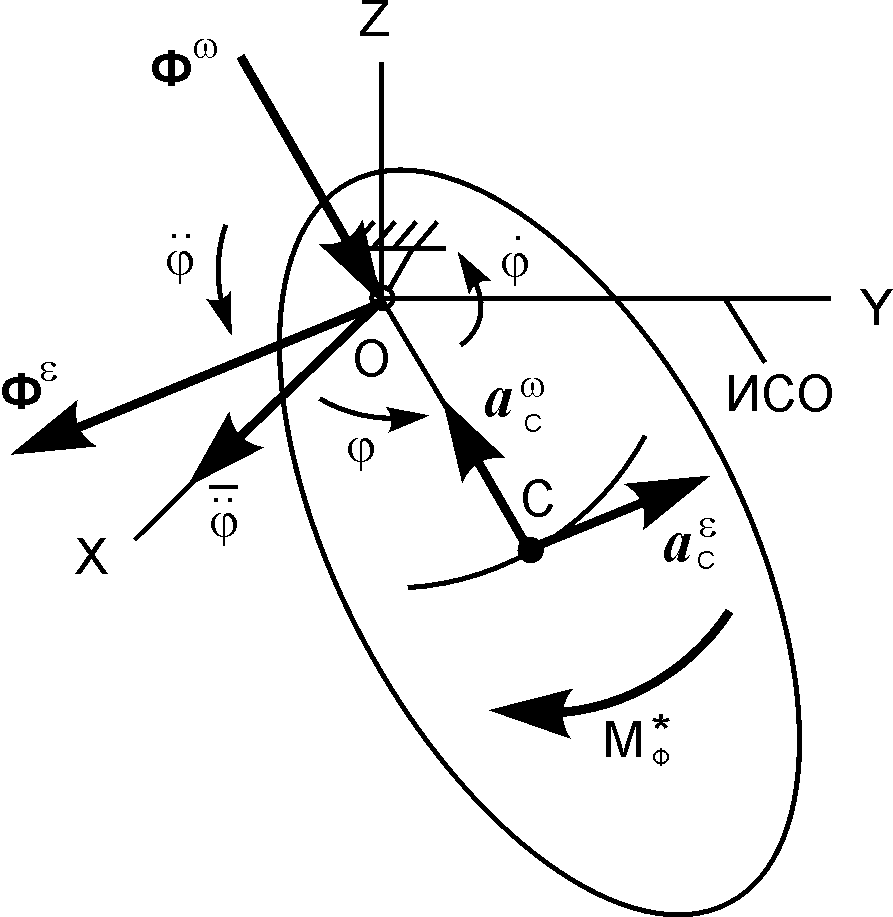

Р

Рис. 5.40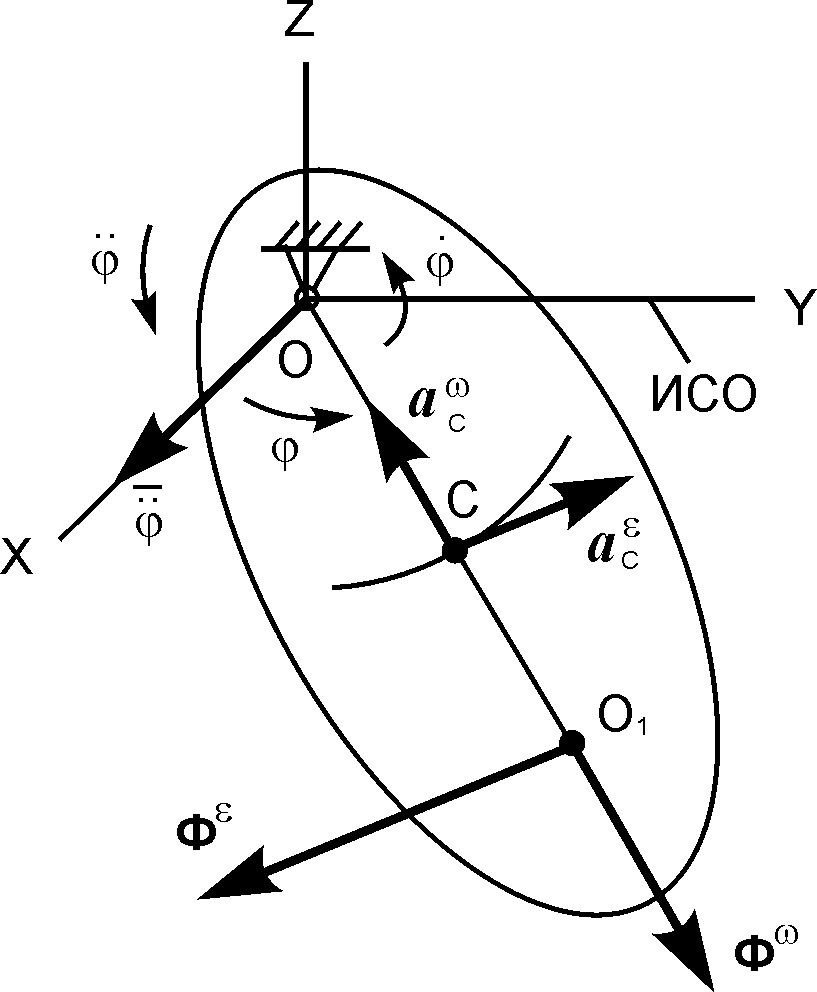

ассмотрим вариант вращательного движения твёрдого тела (рис. 5.40), при котором: Ф^ω = m·( ·CO); Ф^ε = m·(I I·CO); = М^Φ = 0.

В этом случае центробежную и вращательную силы инерции прикладывают в точке О₁, а расстояние ОО₁ определяют по формуле

ОО₁ = J_ОХ/(m·CO),

где J_ОХ – момент инерции тела относительно оси вращения.

В

Рис. 5.41

инженерной практике широкое распространение имеет вариант, при котором ось вращения тела проходит через его центр масс (рис. 5.41).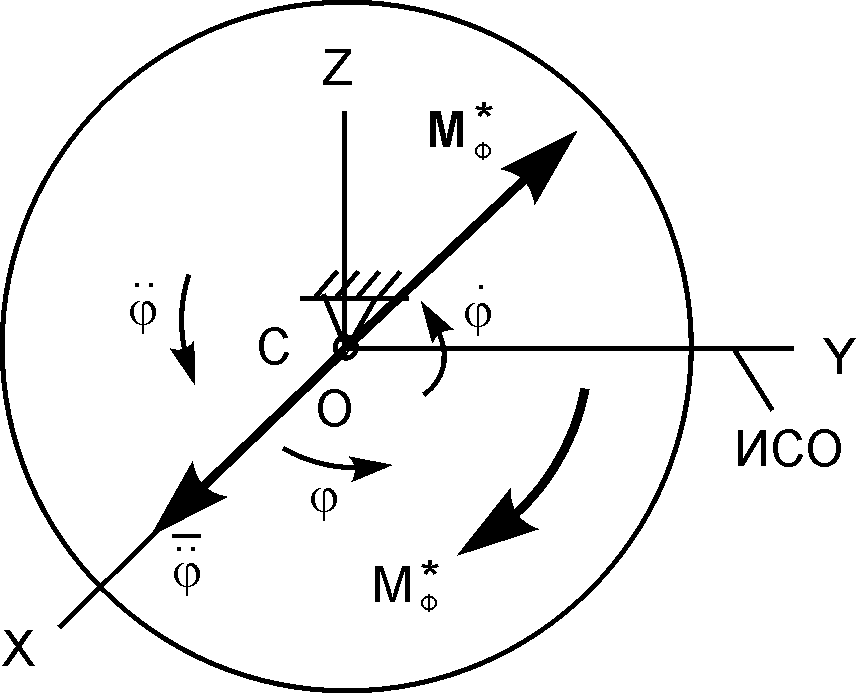

В рассматриваемом случае силы инерции материальных точек твёрдого тела приводятся к моменту М^Ф сил инерции.

М^Ф = J_СХ· I I.

О

Рис. 5.42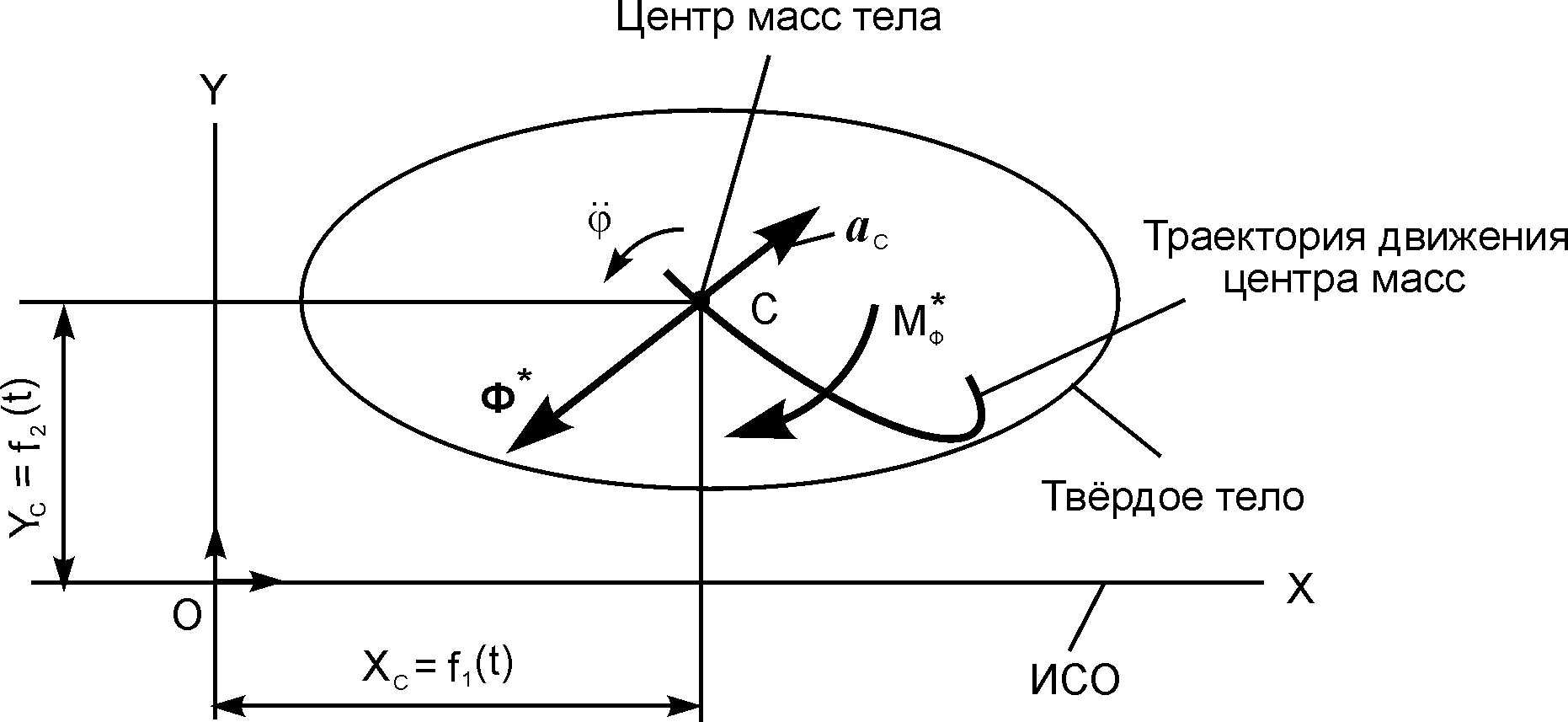

пределим и покажем на рис. 5.42 главный вектор Ф^* сил инерции и момент М^Ф сил инерции при плоскопараллельном движении твёрдого тела.

При таком движении твёрдого тела имеем:

Ф^* = m·a_c; М^Ф = J_CZ·I I,

где J_CZ – момент инерции тела относительно оси CZ вращения, проходящей через центр масс.

Для закрепления изложенного материала студентам рекомендуется выполнить курсовое задание Д 5.