5.6.2. Принцип Даламбера для несвободной

механической системы

Р

Рис. 5.35

ассмотрим движение материальной точки C_i несвободной неизменяемой механической системы под действием активной силы , реакции внешней связи и внутренней силы в инерциальной системе отсчёта OXYZ со скоростью V_Ci и ускорением a_Ci (рис. 5.35).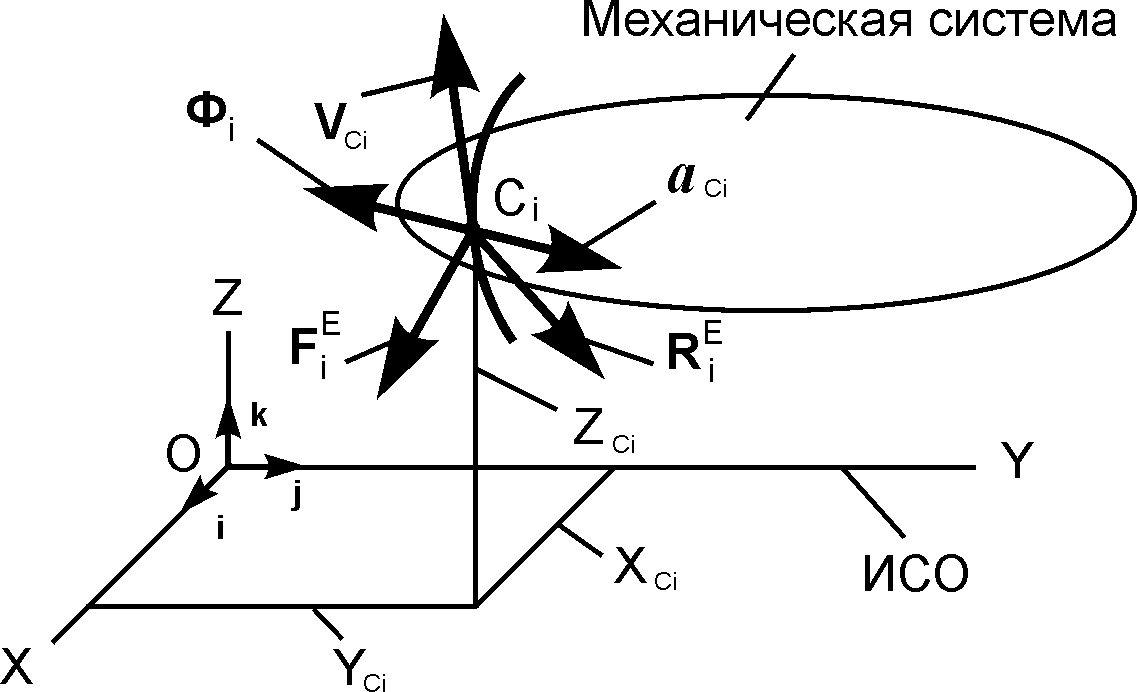

Применим принцип Даламбера для каждой точки C_i неизменяемой механической системы.

+ + + Ф_i = 0,

где Φ_i = – m·a_Ci – сила инерции материальной точки C_i механической системы.

Просуммируем составленные уравнения и получим выражение

Σ + Σ + Σ + ΣФ_i = 0.

Поскольку механическая система неизменяемая, то геометрическая сумма реакций внутренних связей равна нулю (Σ = 0). Тогда получим

Σ + Σ + ΣФ_i = 0.

В любой момент времени для неизменяемой механической системы геометрическая сумма активных сил, реакций внешних связей и сил инерции равна нулю.

Это и есть принцип Даламбера для неизменяемой механической системы.

Этот принцип зачастую записывают в следующем виде:

F^* + R^* + Φ^* = 0,

где F^* = Σ – главный вектор активных сил; R^* = Σ – главный вектор реакций внешних связей; Φ^* = ΣФ_i – главный вектор сил инерции.

В любой момент времени для неизменяемой механической системы геометрическая сумма главных векторов активных сил, реакций внешних связей и сил инерции равна нулю.

Как правило, векторное равенство F^* + R^* + Φ^* = 0, выражающее принцип Даламбера, применяют при рассмотрении поступательного движения твёрдого тела.

Используя метод Пуансо для каждой материальной точки механической системы, приведём произвольно направленные в пространстве активные силы , реакции внешних связей и силы инерции Ф_i к центру масс механической системы (рис. 5.36).

Рис. 5.36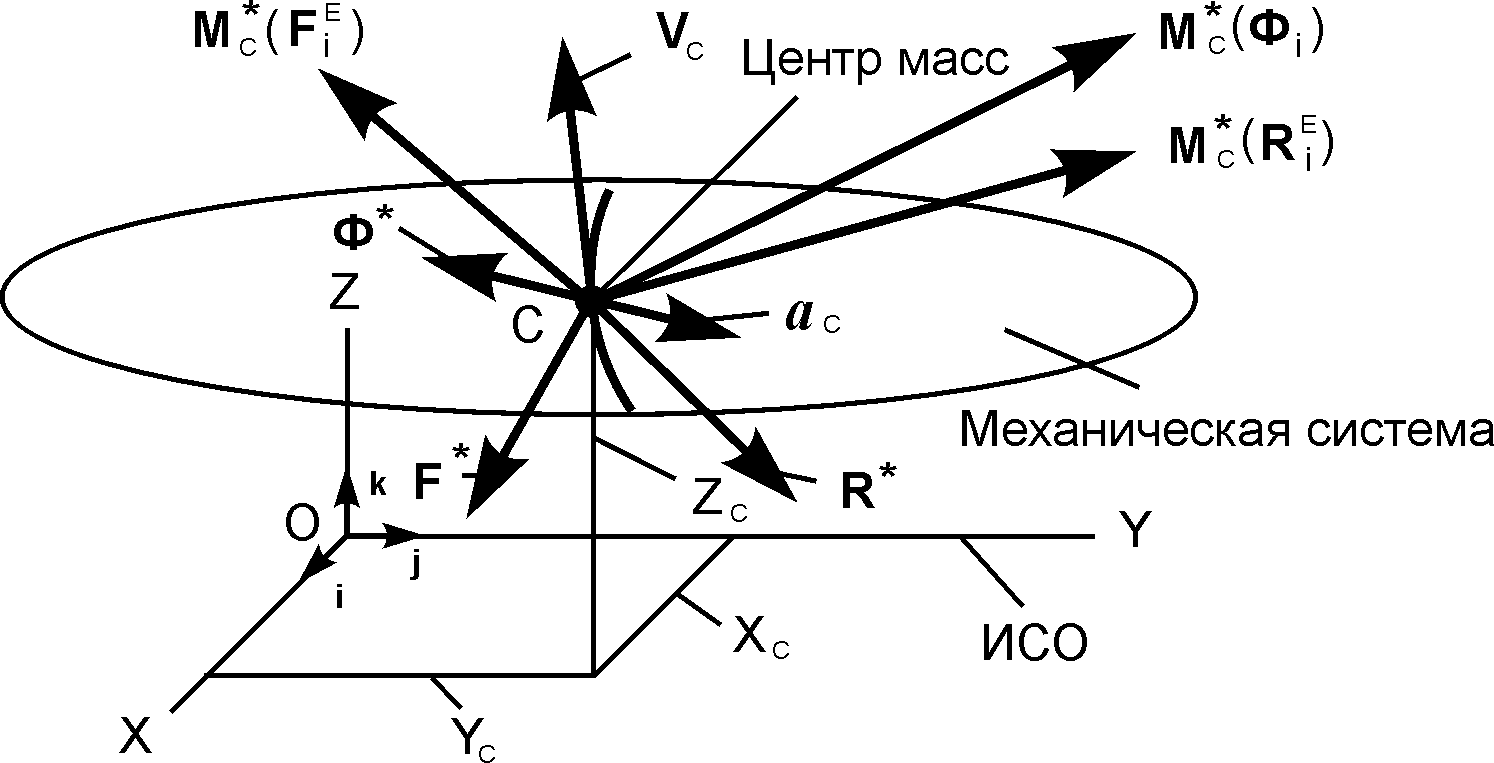

Необходимо отметить, что метод Пуансо справедлив для любой произвольной точки, но, как правило, в инженерной практике за такую точку принимают центр масс твёрдого тела или механической системы.

Согласно методу Пуансо система активных сил , реакций внешних связей и сил инерции Ф_i эквивалентна системе сил (F^*, R^*, Φ^*) и системе присоединённых пар сил с векторными моментами , , (Ф_i), где = Σ – главный момент активных сил относительно центра масс; = Σ – главный момент реакций внешних связей относительно центра масс; (Ф_i) = Σ (Ф_i) – главный момент сил инерции относительно центра масс.

С использованием условных обозначений: F^*, R^*, Φ^*, , , (Ф_i) принцип Даламбера преобразуется в совокупность двух векторных выражений:

F^* + R^*+ Φ^*= 0;

+ + (Ф_i) = 0.

В любой момент времени для движущейся неизменяемой механической системы геометрические суммы главных векторов и главных моментов активных сил, реакций внешних связей и сил инерции относительно произвольного центра (как правило, относительно центра масс) равны нулю.

Спроецируем последние векторные равенства на координатные оси системы отсчёта OXYZ и получим шесть уравнений, выражающих принцип Даламбера в скалярной форме:

+ + = 0;

+ + = 0;

+ + = 0;

= 0;

= 0;

= 0,

где , , – проекции главного вектора активных сил на координатные оси; , , – проекции главного вектора реакций внешних связей на координатные оси; , , – проекции главного вектора сил инерции на координатные оси; , , – проекции главного момента активных сил на координатные оси; , , – проекции главного момента реакций внешних связей на координатные оси; , , – проекции главного момента сил инерции на координатные оси.

В любой момент времени для движущейся неизменяемой механической системы суммы проекций главных векторов активных сил, реакций внешних связей и сил инерции, а также суммы проекций главных моментов активных сил, реакций внешних связей и сил инерции относительно произвольного центра на координатные оси инерциальной системы отсчёта равны нулю.

Как правило, в инженерной практике силы не приводят в одну точку и, следовательно, такими понятиями, как главные векторы сил и главные моменты сил относительно произвольной точки не пользуются, а применяют силы, приложенные в различных точках механической системы. В этом случае принцип Даламбера выражается следующими уравнениями:

Σ + Σ + Σ = 0;

Σ + Σ + Σ = 0;

Σ + Σ + Σ = 0;

Σ + Σ + Σ = 0;

Σ + Σ + Σ = 0;

Σ + Σ + Σ = 0,

где Σ , Σ , Σ – суммы проекций активных сил на координатные оси; Σ , Σ , Σ – суммы проекций реакций внешних связей на координатные оси; Σ , Σ , Σ – суммы проекций сил инерции на координатные оси; Σ , Σ , Σ – суммы моментов активных сил относительно координатных осей; Σ , Σ , Σ – суммы моментов реакций внешних связей относительно координатных осей; Σ , Σ , Σ – суммы моментов сил инерции относительно координатных осей.

В любой момент времени для движущейся неизменяемой механической системы суммы проекций активных сил, реакций внешних связей и сил инерции на координатные оси, а также суммы моментов активных сил, реакций внешних связей и сил инерции относительно координатных осей равны нулю.

Последние математические выражения применяются для механических систем, расположенных в трёхмерном пространстве. Для плоских систем используют двумерное пространство. В таком пространстве принцип Даламбера выражается следующими уравнениями:

Σ + Σ + Σ = 0;

Σ + Σ + Σ = 0;

Σ ) + Σ + Σ = 0,

где Σ ), Σ , Σ – суммы моментов соответственно активных сил, реакций внешних связей и сил инерции относительно произвольной точки А.

В любой момент времени для движущейся неизменяемой механической системы суммы проекций активных сил, реакций внешних связей и сил инерции на координатные оси, а также сумма моментов активных сил, реакций внешних связей и сил инерции относительно произвольной точки равны нулю.

В инженерной практике, как правило, принцип Даламбера применяют для определения реакций внешних связей, наложенных на механическую систему.