Вопросы и задания для самоконтроля

1. Сформулировать определение понятия «работа постоянной силы на прямолинейном перемещении точки её приложения».

2. Сформулировать определение понятия «элементарная работа переменной силы».

3. Записать формулу для определения работы силы тяжести.

4. Сформулировать определение понятия «мощность силы».

5. Сформулировать определение понятия «кинетическая энергия».

6. Записать формулу для определения кинетической энергии материальной точки.

7. Записать формулу для определения кинетической энергии поступательно движущегося твёрдого тела.

8. Записать формулу для определения кинетической энергии вращающегося тела относительно вертикальной оси.

9. Записать формулу для определения кинетической энергии для твёрдого тела, совершающего плоскопараллельное движение.

10. Записать формулу для определения кинетической энергии механической системы.

11. Записать формулу, выражающую теорему об изменении кинетической энергии неизменяемой механической системы.

5.6. Принцип Даламбера для материальной точки и механической системы

5.6.1. Принцип Даламбера для несвободной

материальной точки

Рассмотрим движение несвободной материальной точки под действием активных сил и реакций внешних связей в инерциальной системе отсчёта OXYZ (рис. 5.34).

Следует отметить, что на точку могут действовать несколько активных сил и реакций внешних связей. Однако на рис. 5.34 показаны только по одной из этих сил.

Основное уравнение динамики точки имеет вид

m·a = Σ + Σ .

Перенесём произведение m·a из левой части рассматриваемого уравнения в правую его часть:

Σ + Σ – m·a = 0.

Введём условное обозначение Ф = – m·a. Назовём Ф силой инерции материальной точки.

С

Рис. 5.34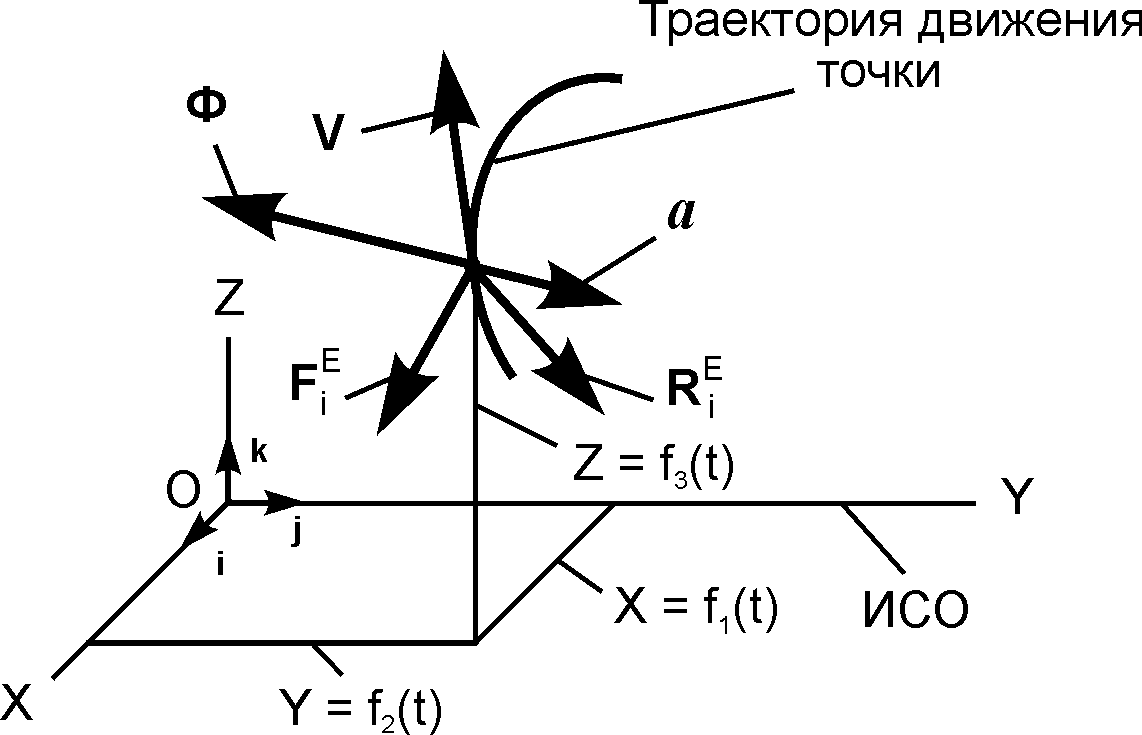

ила инерции материальной точки – величина, равная произведению массы точки на её ускорение и направленная противоположно этому ускорению.

Как вектор сила инерции Ф имеет размерность [Н] и характеризуется тремя элементами: точкой приложения (приложена в точке, движение которой рассматривается); направлением (направлена в сторону, противоположную направлению ускорения a); модулем Ф, который определяется по формуле Ф = m·a.

Исходя из изложенного выше, последнее векторное равенство представим в следующем виде:

Σ + Σ + Ф = 0.

Это векторное уравнение и выражает принцип Даламбера для несвободной материальной точки.

В любой момент времени для движущейся несвободной материальной точки геометрическая сумма активных сил, реакций внешних связей и силы инерции равна нулю.

По существу, основное уравнение динамики точки (m·a = Σ + Σ ) преобразовано к другому виду (Σ + Σ + Ф = 0), который широко применяется в статике механических систем.

Поскольку силовой многоугольник, построенный на векторах активных сил , реакций внешних связей и силы инерции Ф замкнут, то суммы проекций этих сил на координатные оси системы отсчёта OXYZ равны нулю. Спроецируем векторное равенство (Σ + Σ + Ф = 0) на координатные оси инерциальной системы отсчёта и получим следующие равенства:

Σ + Σ + Ф_ОХ = 0;

Σ + Σ + Ф_OY = 0;

Σ + Σ + Ф_OZ = 0.

Сумма проекций активных сил, реакций внешних связей и силы инерции на координатные оси инерциальной системы отсчёта равна нулю.

Последние уравнения зачастую называют уравнениями динамического равновесия материальной точки, в отличие от уравнений (Σ + Σ = 0; Σ + Σ = 0; Σ + Σ = 0) статического равновесия.

В действительности сила инерции материальной точки приложена не к ней, а к телу, взаимодействующему с рассматриваемой точкой. Приложение силы инерции к точке является лишь условным приёмом, сводящим задачу динамики по форме решения к задаче статики.

Благодаря простоте, принцип Даламбера получил широкое применение во многих инженерных дисциплинах. В ряде случаев он обеспечивает наиболее простое и удобное решение задач динамики.