5.2.2. Теорема об изменении количества движения

механической системы

Рассмотрим движение неизменяемой механической системы под действием активных сил , реакций внешних связей и внутренних сил в инерциальной системе отсчёта OXYZ (рис. 5.4).

Количество движения механической системы – величина, равная сумме количеств движения всех материальных точек, образующих механическую систему.

Количество движения K механической системы определяют по формуле

K = Σm_Ci·V_Ci = m·V_C.

Это выражение показывает, что вектор количества движения механической системы равен произведению массы системы на скорость её центра масс.

Проецируя последнее векторное равенство на координатные оси, получим:

K_OX = m·V_COX; K_OY = m·V_COY; K_OZ = m·V_COZ,

где V_COX, V_COY, V_COZ – проекции скорости центра масс механической системы на координатные оси.

Проекция количества движения механической системы на каждую координатную ось равна произведению массы системы на проекцию скорости центра масс на эту же ось.

Рис. 5.4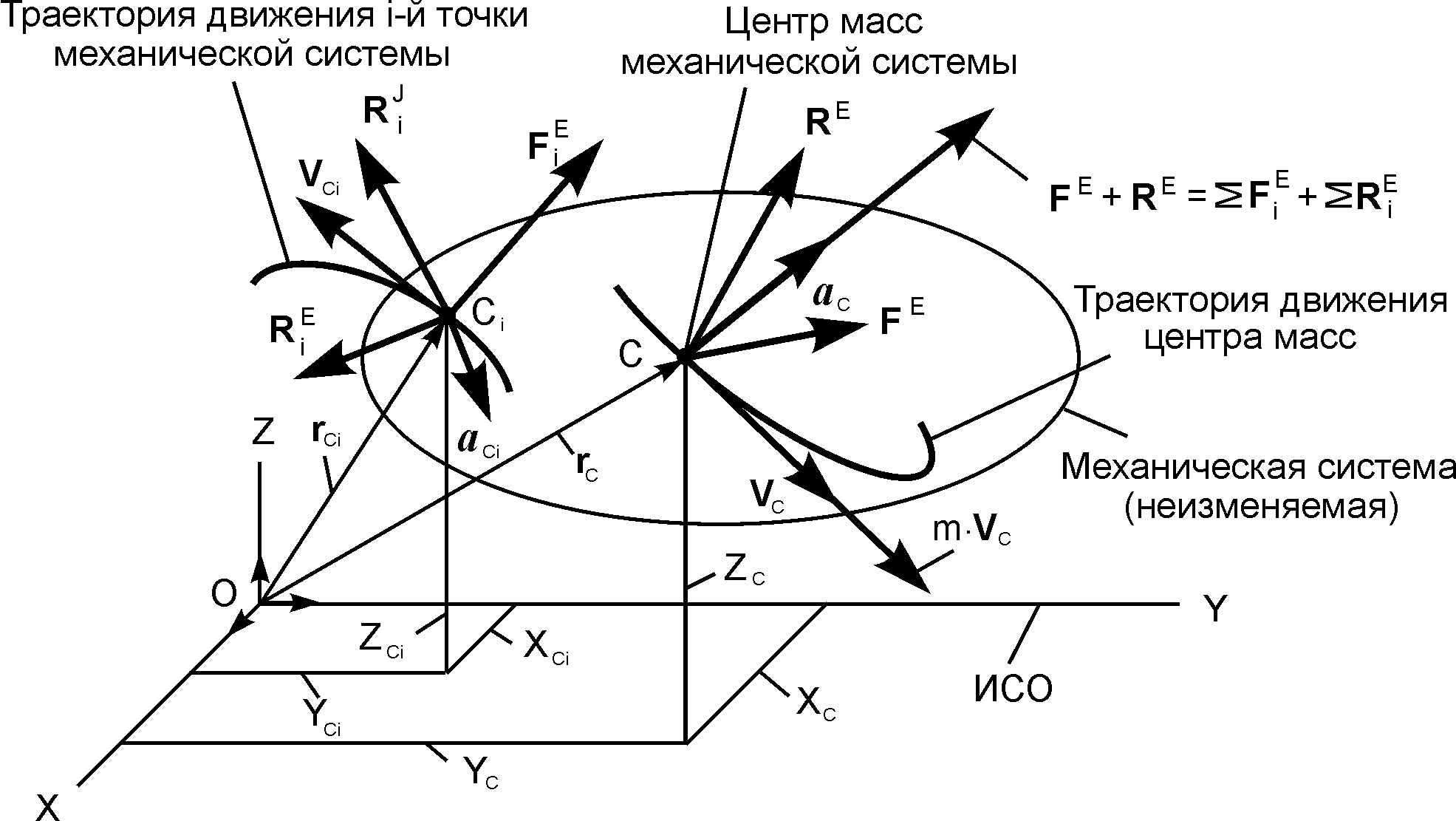

Теорема об изменении количества движения механической системы выражается векторным равенством

dK/dt = Σ + Σ .

Производная по времени от количества движения механической системы равна геометрической сумме активных сил и реакций внешних связей.

Последнему векторному равенству соответствует три уравнения в проекциях на координатные оси:

dK_OX/dt = Σ + Σ ;

dK_OY/dt = Σ + Σ ;

dK_OZ/dt = Σ + Σ ,

где dK_OX/dt, dK_OY/dt, dK_OZ/dt – производные по времени от проекций количества движения механической системы на соответствующие координатные оси системы отсчёта.

Производная по времени от проекции количества движения механической системы на координатную ось равна сумме проекций активных сил и реакций внешних связей на ту же ось.

Необходимо отметить, что изменение количества движения механической системы вызывается только внешними силами, к которым относятся активные силы и реакции внешних связей.

Следствия из теоремы

1. Если геометрическая сумма внешних сил, приложенных к механической системе за рассматриваемый промежуток времени, равна нулю (Σ + Σ = 0), то количество движения механической системы постоянно: K = const.

Действительно, если Σ + Σ = 0, то dK/dt = 0 и, следовательно, K = m·V_С = const.

2. Если сумма проекций активных сил и реакций внешних связей на координатную ось за рассматриваемый промежуток времени равна нулю, то проекция количества движения неизменяемой механической системы на эту ось постоянна.

Так, например, если Σ + Σ = 0, то dK_ОХ/dt = 0 и, таким образом, K_ОХ = m·V_СОХ = const.

Следствия из теоремы об изменении количества движения механической системы выражают закон сохранения количества движения системы.

Так как для заочной формы обучения курсовых заданий на использование теоремы об изменении количества движения неизменяемой механической системы не предусмотрено, то и примеры решения таких задач в данном учебно-методическом пособии не приведены.