Вопросы и задания для самоконтроля

1. Записать формулу для определения модуля силы упругости пружины.

2. Записать дифференциальное уравнение свободных колебаний точки.

3. Записать уравнения свободных колебаний точки.

4. Сформулировать определение понятия «амплитуда свободных колебаний точки».

5. Сформулировать определение понятия «период свободных колебаний точки».

6. Сформулировать определение понятия «циклическая частота свободных колебаний точки».

7. Записать дифференциальное уравнение затухающих колебаний точки.

8. Записать уравнения затухающих колебаний точки.

9. Сформулировать определение понятия «период затухающих колебаний точки».

10. Сформулировать определение понятия «амплитуда затухающих колебаний точки».

11. Какие колебания называют колебаниями с малым сопротивлением внешней среды?

12. Записать уравнения апериодического движения точки.

13. Под действием каких сил происходят вынужденные колебания материальной точки?

14. Записать формулу для определения периода возмущающей силы.

15. Записать дифференциальное уравнение движения точки под действием восстанавливающей и возмущающей сил.

16. Записать уравнение вынужденных колебаний малой частоты.

17. Записать уравнение вынужденных колебаний большой частоты.

18. Записать условие, при котором происходит явление резонанса.

19. Записать дифференциальное уравнение движения точки, происходящее под действием восстанавливающей силы, возмущающей силы, изменяющейся по периодическому закону, и силы сопротивления движению, пропорциональной первой степени скорости.

3. ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ ТОЧКИ

3.1. Дифференциальные уравнения относительного

движения материальной точки.

Переносная и кориолисова силы инерции

Два первых закона классической механики и полученные на их основе уравнения справедливы при движении точки в инерциальной системе отсчёта (ИСО). Существует ряд технических задач, в которых рассматривают движение материальной точки в подвижной системе отсчёта (ПСО), которая в общем случае не является инерциальной.

Инерциальная система отсчёта – система отсчёта, по отношению к которой изолированная материальная точка находится в покое или движется равномерно и прямолинейно.

Система отсчёта, не обладающая этим свойством, называется неинерциальной системой отсчёта

Рассмотрим движение материальной точки под действием активных сил F_i^Е и реакций R_i^Е относительно подвижной неинерциальной системы отсчёта OXYZ (рис. 3.1).

Напомним некоторые понятия кинематики, используемые в данном разделе динамики точки.

Движение точки по отношению к неподвижной системе отсчёта O₁X₁Y₁Z₁ называется абсолютным и характеризуется абсолютной скоростью V и абсолютным ускорением a. Положение точки на траектории абсолютного движения определяется тремя зависящими от времени координатами, которые называются уравнениями абсолютного движения:

X₁ = f₁(t); Y₁ = f₂(t); Z₁ = f₃(t).

Неподвижная система отсчёта O₁X₁Y₁Z₁ является инерциальной. В этой системе отсчёта основное уравнение динамики имеет вид

m·a = ΣF_i^Е + ΣR_i^Е,

где F_i^Е – активная сила; R_i^Е – реакция внешней связи.

Д

Рис. 3.1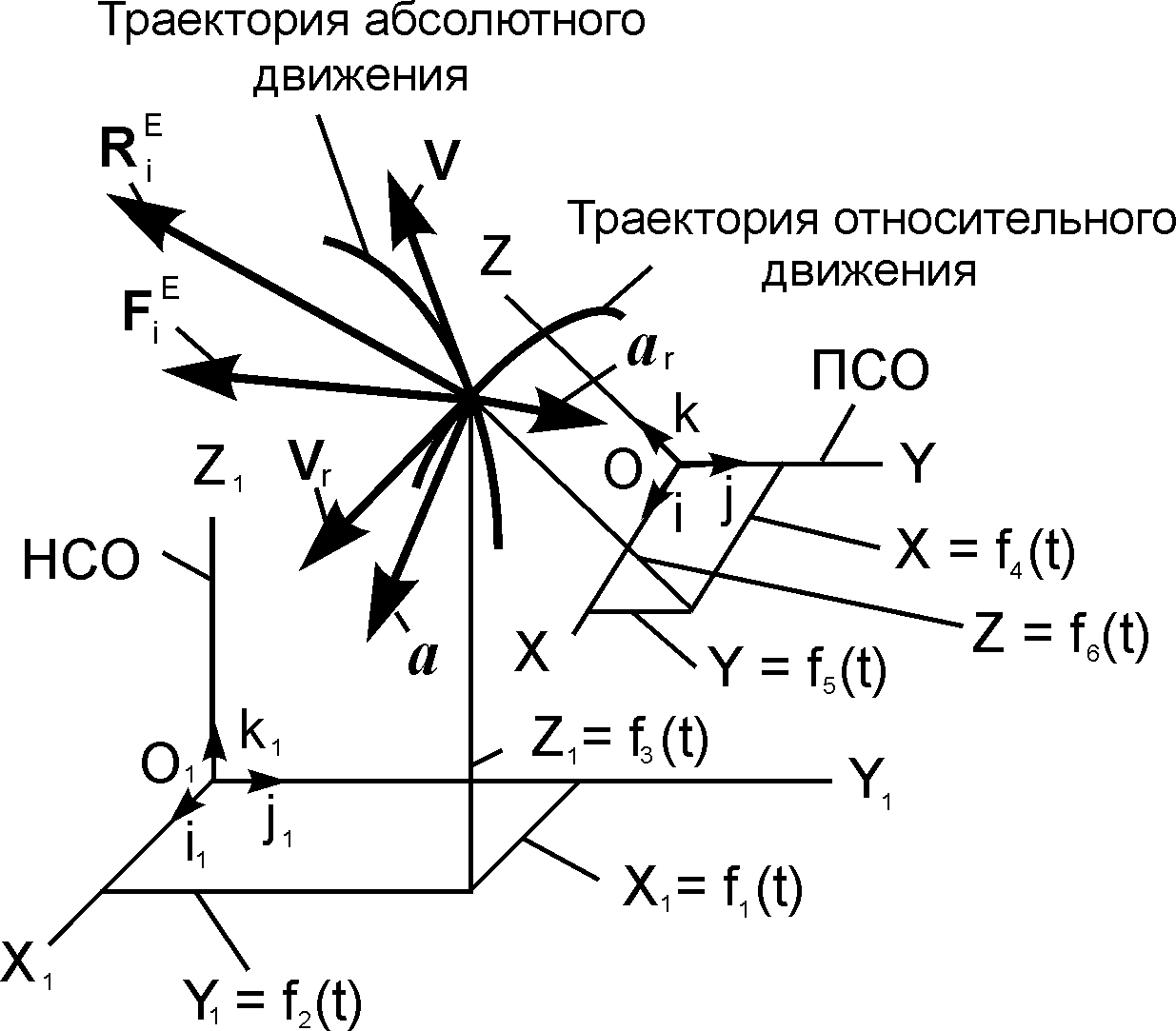

вижение точки по отношению к подвижной системе отсчёта OXYZ называется относительным и характеризуется относительной скоростью V_r и относительным ускорением a_r. Положение точки на траектории относительного движения определяется тремя зависящими от времени координатами, которые называются уравнениями относительного движения:

X = f₄(t); Y = f₅(t); Z = f₆(t).

Подвижная система отсчёта OXYZ не является инерциальной. Применение в чистом виде первого и второго законов классической механики в ПСО неправомерно.

Рассмотрим переносное движение точки (рис. 3.2) и напомним суть некоторых понятий кинематики, используемых в этом разделе динамики.

Если координаты точки в ПСО постоянны (Х = C₁ = const; Y = C₂ = const; Z = C₃ = const), то движение этой точки вместе с ПСО по отношению к неподвижной системе отсчёта называют переносным движением. Это движение характеризуется переносной скоростью V_e и переносным ускорением a_e. Положение точки на траектории переносного движения определяется тремя зависящими от времени координатами, которые называют уравнениями переносного движения:

= f₇(t) = f₈(t) = f₉(t)

И

Рис. 3.2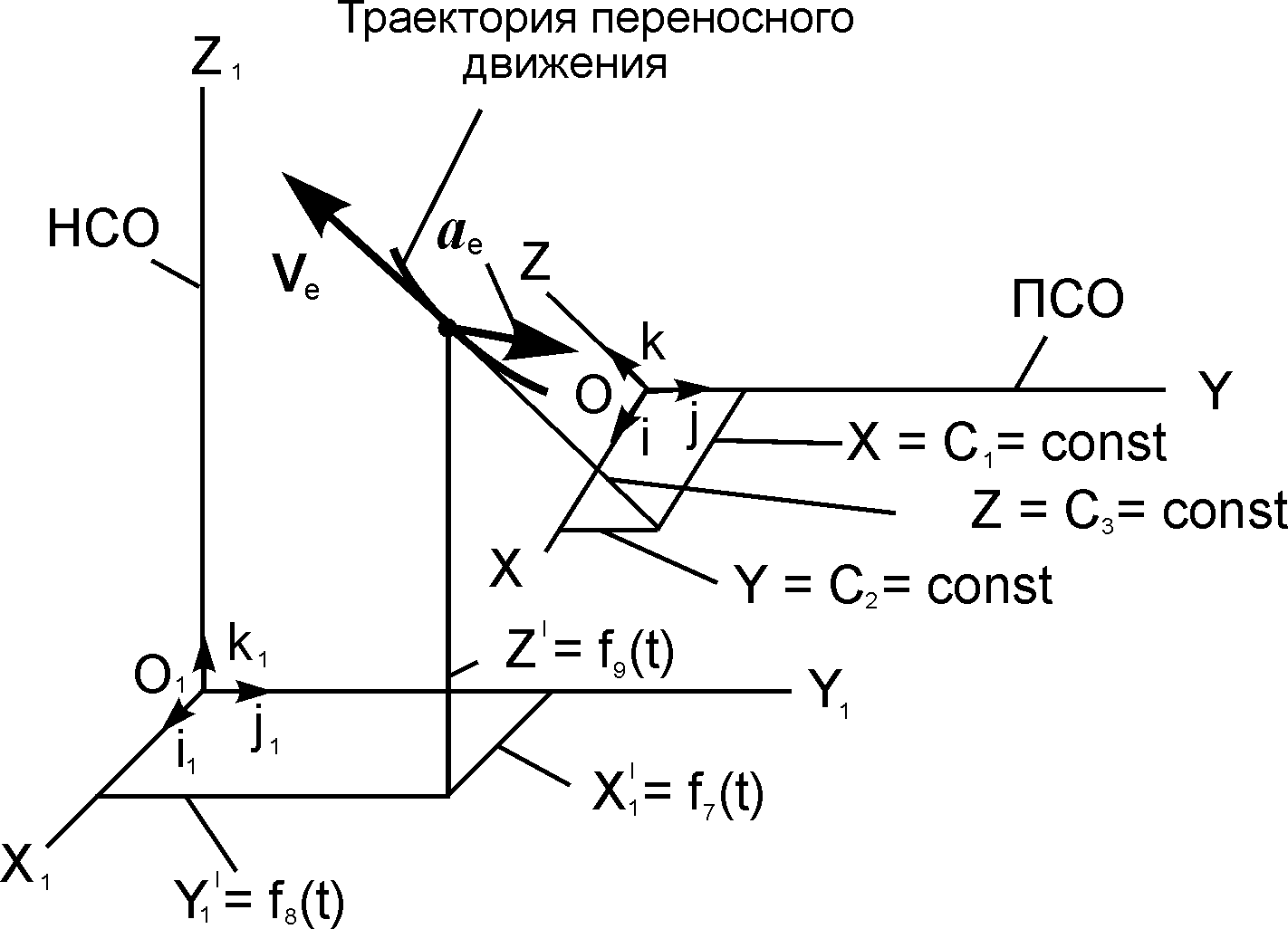

з курса кинематики известно, что абсолютное ускорение a точки определяют по формуле

a = a_r + a_e + a_c,

где a_r – относительное ускорение; a_e – переносное ускорение; a_c – ускорение Кориолиса.

Ускорение Кориолиса определяют по формуле

a_c = 2( × V_r),

где – вектор угловой скорости переносного вращения.

Модуль кориолисова ускорения находят по формуле

a_c = 2ω_e·V_r·sin( ,V_r),

где ω_е = I I – модуль угловой скорости переносного вращения.

Кориолисово ускорение равно нулю в трех случаях:

1. если ω_e = 0, т. е. в случае поступательного переносного движения или в момент обращения в нуль угловой скорости непоступательного переносного движения;

2. если V_r = 0, т. е. в случае относительного покоя точки или в момент равенства нулю относительной скорости движущейся точки;

3. если sin( ,V_r) = 0, т. е. в случае, когда вектор относительной скорости V_r и вектор переносной угловой скорости параллельны.

Направление кориолисова ускорения определяется по правилу векторного произведения. Согласно этому правилу вектор a_c одновременно перпендикулярен векторам и V_r. При этом a_c направлено в сторону, откуда поворот вектора к вектору V_r для совмещения их направлений виден происходящим против хода часовой стрелки. Поворот осуществляется на угол меньше 180^о.

Направление ускорения Кориолиса находят также по правилу Жуковского: для определения направления ускорения Кориолиса необходимо относительную скорость V_r точки спроецировать на плоскость, перпендикулярную оси вращения, и повернуть эту проекцию в той же плоскости на угол 90^о в сторону переносного вращения.

Если подставим абсолютное ускорение a = a_r + a_e + a_c в основное уравнение динамики точки m·a = ΣF_i^Е + ΣR_i^Е, то получим

m·(a_r + a_e + a_c) = ΣF_i^Е + ΣR_i^Е.

Разрешим это уравнение относительно m·a_r:

m·a_r = ΣF_i^Е + ΣR_i^Е – m·a_e – m·a_c.

Введём два вектора: Ф_е = – m·a_e; Ф_с = – m·a_c. Эти векторы назовем переносной и кориолисовой силами инерции.

При исследовании движения механических систем в теоретической механике используют следующие понятия.

Сила инерции – величина, равная произведению массы материальной точки на её ускорение и направленная противоположно этому ускорению.

Переносная сила инерции при рассмотрении движения материальной точки в неинерциальной системе отсчёта – величина, равная произведению массы точки на её переносное ускорение и направленная противоположно этому ускорению.

Кориолисова сила инерции при рассмотрении движения точки в неинерциальной системе отсчёта – величина, равная произведению массы точки на её кориолисово ускорение и направленная противоположно этому ускорению.

Используя понятия переносной и кориолисовой сил инерции, получим

m·a_r = ΣF_i^Е + ΣR_i^Е + Ф_е + Ф_с.

Последнее выражение называют дифференциальным уравнением относительного движения точки в векторной форме или основным уравнением динамики относительного движения.

Произведение массы m точки на её относительное ускорение a_r равно геометрической сумме активных сил F_i^Е, реакций внешних связей R_i^Е, переносной силы инерции Ф_е и кориолисовой силы инерции Ф_с.

Проецируя последнее векторное равенство на координатные оси ПСО, получим дифференциальные уравнения относительного движения точки:

m· = Σ + Σ + + ;

m· = Σ + Σ + + ;

m· = Σ + Σ + + .

Произведение массы точки на проекцию её относительного ускорения на координатную ось ПСО равно сумме проекций активных сил, реакций внешних связей и переносной и кориолисовой сил инерции на ту же ось.

С

Рис. 3.3

илы инерции Ф_е, Ф_с направлены противоположно ускорениям a_e, a_c (рис. 3.3).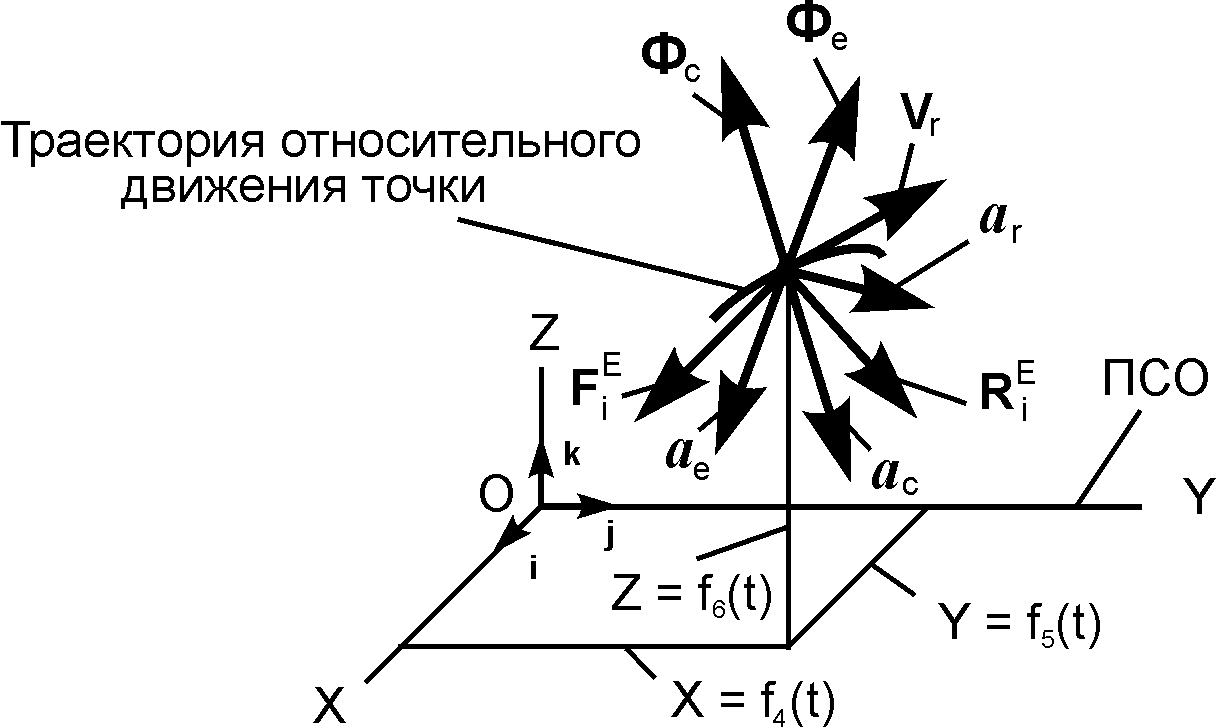

Дифференциальные уравнения относительного движения точки

m· = Σ + Σ + + ;

m· = Σ + Σ + + ;

m· = Σ + Σ + +

отличаются от дифференциальных уравнений движения точки в инерциальной системе отсчёта (см. раздел 1)

m· = Σ + Σ ;

m· = Σ + Σ ;

m· = Σ + Σ

наличием в правой части этих уравнений проекций на соответствующие координатные оси переносной и кориолисовой сил инерции.