2.8. Алгоритм решения задач на колебания материальной точки

Алгоритм решения задач динамики несвободной материальной точки при её колебательном движении содержит следующие действия.

1. В механической системе выделяют материальную точку, движение которой рассматривают.

2. Выбирают инерциальную систему отсчёта, начало которой помещают в положение статического равновесия материальной точки.

3. В выбранной системе отсчёта точку изображают в произвольный момент времени таким образом, чтобы она имела положительную координату и двигалась в сторону её увеличения ускоренно.

4. По исходным данным задачи определяют и изображают на рисунке начальные условия движения: Y₀; .

5. К точке прикладывают активные (задаваемые) силы F_i^E.

6. Согласно аксиоме связей эти связи отбрасывают и действие их заменяют соответствующими реакциями R_i^E связей.

ПРИМЕЧАНИЕ.

Если точка движется не по горизонтали, то рассматривают равновесие материальной точки. Из условия равновесия (ΣF_i^E + ΣR_i^E = 0) определяют деформацию пружины при действии на неё постоянной системы активных сил F_i^Е.

7. Записывают дифференциальные уравнения движения точки, приводят их к стандартному виду и записывают решения:

а) + k²·Y = 0; Y = A·sin(k·t + β) – свободные колебания;

б) + 2n· + k²·Y = 0;

если n < k, то Y = a·(e^-nt)·sin(k^*·t + β) – затухающие колебания;

если n = k, то Y = (e^-nt)·(C₁·t + C₂) – апериодическое движение;

если n > k, то Y = (e^-nt)·(C₁· ^)·t + C₂· ^)·t) –

– апериодическое движение;

в) + k²·Y = h·sin(p·t + δ);

если р < k, то Y = A·sin(k·t + β) + (h/(k² – p²))·sin(p·t + δ);

если р > k, то Y = A·sin(k·t + β) + (h/(р² – k²))·sin(p·t + δ – π) –

– вынужденные колебания соответственно малой и

большой частоты под действием

восстанавливающей и возмущающей сил;

г) + 2n· + k²·Y = h·sin(p·t + δ);

если n < k, то Y = a ·(e^-nt)·sin(k^*·t + β) + A_c·sin(p·t + δ – ε);

если n = k, то Y = (e^-nt)·(C₁·t + C₂) + A_c·sin(p·t + δ – ε);

если n > k, то

Y = (e^-nt)·(C₁· ^)·t + C₂· ^)·t) + A_c·sin(p·t + δ –ε).

8. По начальным условиям движения точки определяют постоянные интегрирования по формулам, приведённым в разделе 2 данного учебно-методического пособия.

9. Полученное решение Y = f(t) иллюстрируется соответствующими графиками.

2.9. Пример решения задачи на свободные колебания груза по гладкой наклонной поверхности

Условие задачи.

Н

Рис. 2.18

айти уравнение движения груза D массой m по гладкой наклонной плоскости, составляющей с горизонтом угол α, с момента соприкосновения груза с системой пружин, предполагая, что при дальнейшем движении груз от пружины не отделяется (рис. 2.18).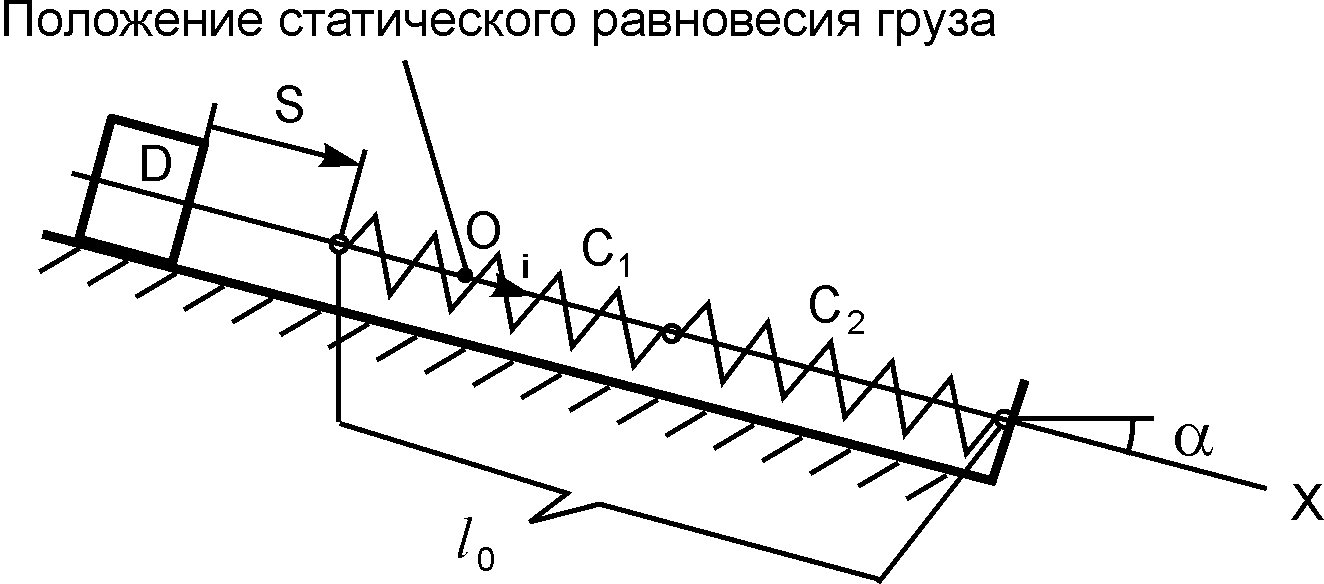

Пройдя без начальной скорости по наклонной плоскости (α = 30^о) расстояние S = 0,1 м, груз D (m = 4 кг) ударяется о недеформированные последовательно соединённые пружины, имеющие коэффициенты жёсткости с₁ = 48 Н/см и с₂ = 24 Н/см.

Движение груза отнести к оси ОХ, наклоненной к горизонтальной поверхности под углом α, приняв за начало отсчёта положение покоя груза (при статической деформации пружин).

Решение.

Так как груз будет совершать поступательное движение, то его можно рассматривать как материальную точку, совершающую колебания в заданной системе отсчёта ОХ, начало которой находится в положении статического равновесия груза (рис. 2.19).

Н

Рис. 2.19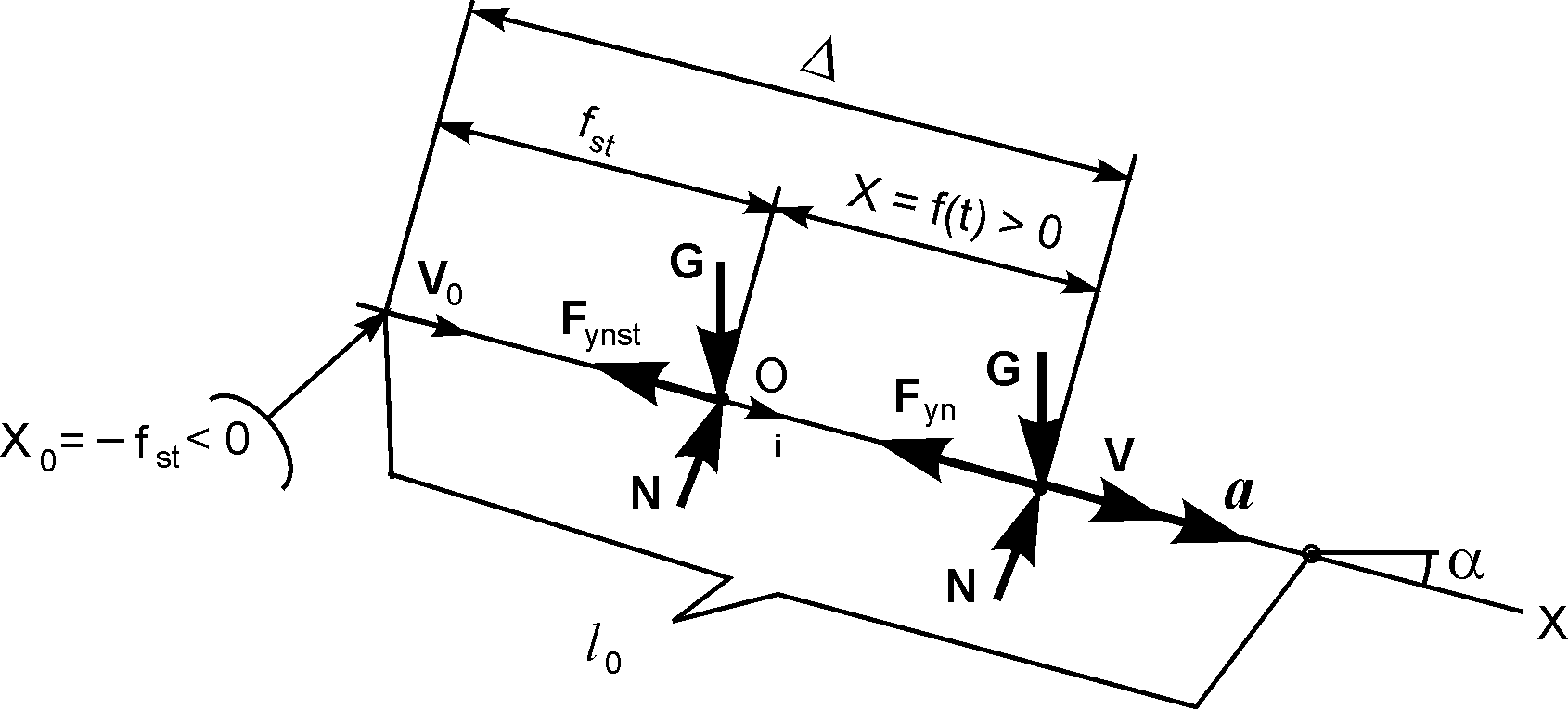

а рис. 2.19 использованы следующие условные обозначения: l₀ – длина недеформированной пружины с эквивалентной жёсткостью «с»; f_st – деформация пружины в положении статического равновесия материальной точки; G – сила тяжести; N – нормальная реакция гладкой поверхности; F_ynst – сила упругости пружины в положении статического равновесия материальной точки; X₀ – начальная координата точки; V₀ – начальная скорость точки; X = f(t) – текущее значение координаты точки; V, a – текущие значения скорости и ускорения точки; F_yn – текущее значение силы упругости эквивалентной пружины; Δ – текущее значение деформации эквивалентной пружины.

Так как жесткость пружины имеет размерность [Н/м], то: с₁ = 48 Н/см = 4800 Н/м; с₂ = 24 Н/см = 2400 Н/м. Заменим последовательно соединённые пружины с жёсткостями с₁, с₂ одной эквивалентной пружиной с жёсткостью «с».

с = (с₁·с₂)/(с₁+ с₂) = (4800·2400)/(4800 + 2400) = 1600 Н/м.

ПРИМЕЧАНИЕ.

При параллельном соединении пружин жёсткость эквивалентной пружины определяют по формуле с = с₁ + с₂.

Для определения величины f_st рассмотрим равновесие материальной точки. Геометрическое условие равновесия точки имеет вид ΣF_i^E + ΣR_i^E = G + N + F_ynst = 0. Спроецируем это векторное равенство на ось ОХ.

Σ + Σ = 0 = G·sin(α) – F_ynst = m·g·sin(α) – c·f_st = 0.

Отсюда имеем

f_st = m·g·sin(α)/с = (4·9,81·0,5)/1600 = 0,012 м.

В момент соприкосновения груза с пружиной начальная координата X₀ = – f_st = – 0,012 м.

Для определения начальной скорости V₀ рассмотрим движение груза, приняв его за материальную точку, в системе отсчёта О₁Х₁ (рис. 2.20).

Рис. 2.20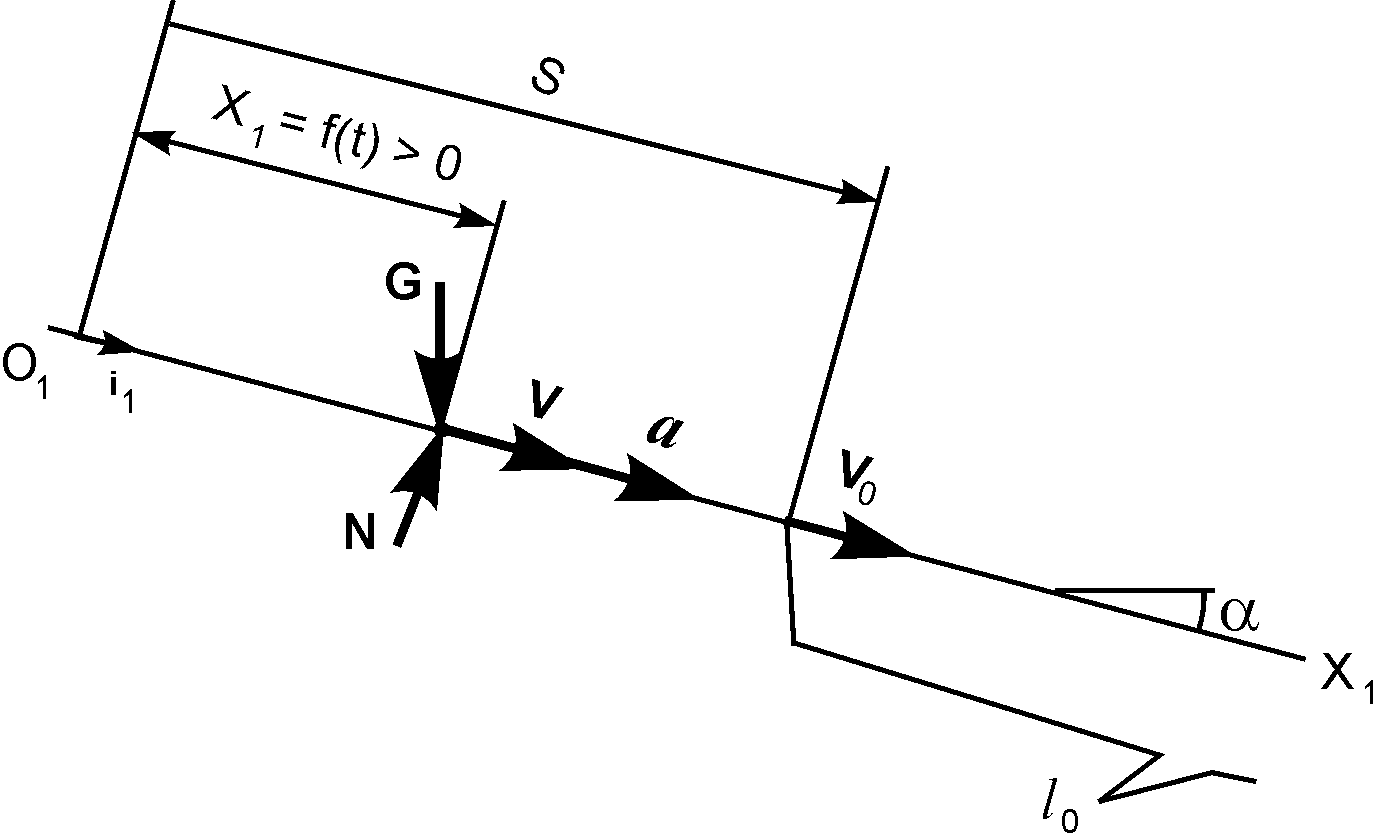

Согласно задаче начальные условия движения груза имеют вид: Х₁₀ = 0; = 0.

Запишем дифференциальные уравнения движения груза и дважды проинтегрируем его:

m· = G·sin(α) = m·g·sin(α);

= g·sin(α)·t + С₁;

Х₁ = g·sin(α)·(t²/2) + С₁·t + С₂.

Определим постоянные интегрирования. Поскольку Х₁₀ = 0 и = 0, то имеем С₁ = 0 и С₂ = 0. Тогда: = g·sin(α)·t; Х₁ = g·sinα·(t²/2).

За время t_s груз проходит расстояние S и соприкасается с пружиной. Исходя из этого, получим

V₀ = g·sin(α)·t_s ; S = g·sin(α)·((t_s)²/2).

Решая эти уравнения, получим:

t_s = = = 0,201 c;

V₀ = 9,81·0,5·0,201 = 0,990 м/с.

Таким образом, начальные условия движения точки при её контакте с пружиной определены: X₀ = – 0,012 м; = 0,990 м/с.

Рассмотрим движение материальной точки в системе отсчёта ОХ в произвольный момент времени (см. рис. 2.19). На точку действуют следующие силы: G, N, F_yn. Необходимо отметить, что модуль силы F_yn = с·Δ является переменной величиной, так как деформация Δ пружины зависит от координаты точки Х = f(t), которая является функцией от времени.

F_yn = c·Δ = c·(f_st + X).

Основное уравнение динамики для точки имеет вид

m·a = ΣF_i^E + ΣR_i^E = G + N + F_yn.

Запишем дифференциальное уравнение движения точки:

m· = G·sin(α) – F_yn =

= m·g·sin(α) – c·(f_st + X) = m·g·sin(α) – c·f_st – c·X.

Из условия равновесия точки было получено равенство

m·g·sin(α) – c·f_st = 0.

Используя это равенство, получим

m· + c·X = 0 или + (c/m)·X = 0.

Последнее выражение приведём к стандартному виду:

+ k² ·X = 0,

где – циклическая частота свободных колебаний.

= = 20 с^-1.

Таким образом, материальная точка совершает свободные колебания около положения своего статического равновесия. Уравнение этого движения имеет вид

Х = A·sin(k·t + β),

где А – амплитуда свободных колебаний; β – начальная фаза.

= = 0,050 м;

sin(β) = Х₀/A = – 0,012/0,050 = – 0,239;

cos(β) = /(A·k) = 0,990/(0,050·20) = 0,972.

Поскольку sin(β) < 0, a cos(β) > 0, то величину угла β можно определить по формуле

β = π – α,

где α = аrcsin(0,239) = 0,237 рад или α = аrccos(0,972) = 0,237 рад.

При этом значении величины угла α начальная фаза β имеет значение

β = 3,14 – 0,237 = 2,903 рад.

Уравнение колебательного движения груза имеет вид

Х = 0,05·sin(20·t + 2,903).

Г

Рис. 2.21

рафик движения этого груза приведён на рис. 2.21.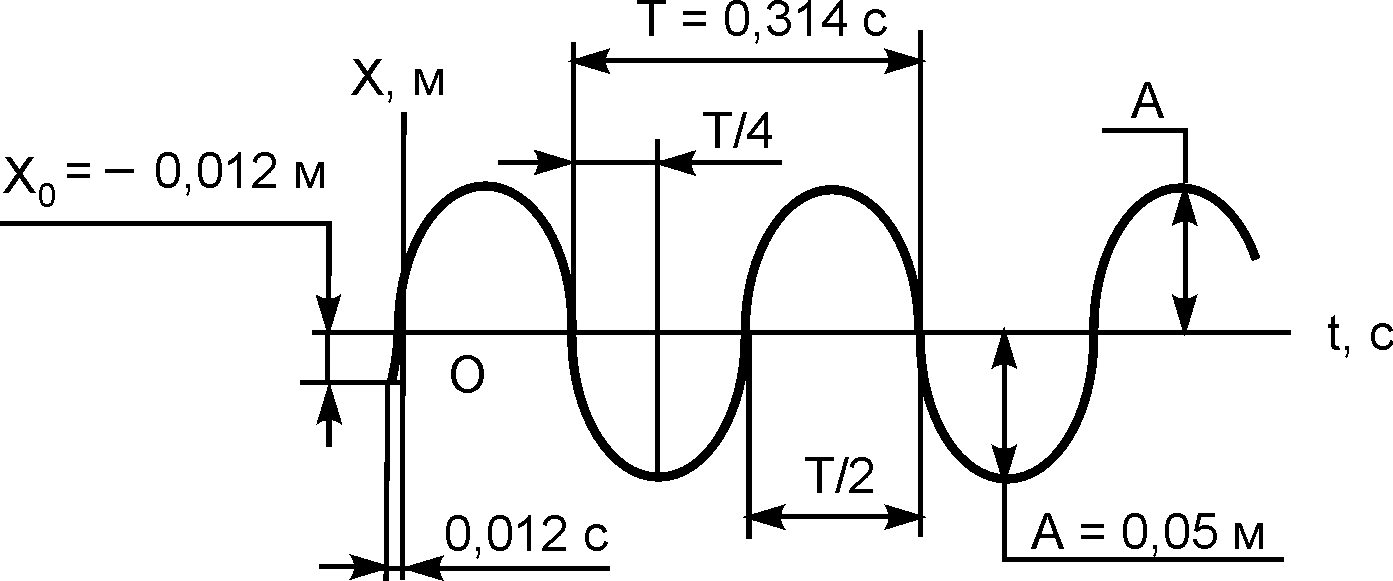

Таким образом, задача решена. Установлено, что груз совершает гармонические колебания около положения своего статического равновесия.