2.7. Влияние сопротивлений движению на вынужденные колебания материальной точки

Р

Рис. 2.15

ассмотрим движение материальной точки на гладкой горизонтальной поверхности, происходящее под действием постоянной системы сил, восстанавливающей силы, силы сопротивления движению, пропорциональной первой степени скорости, и возмущающей силы, изменяющейся по периодическому закону (рис. 2.15).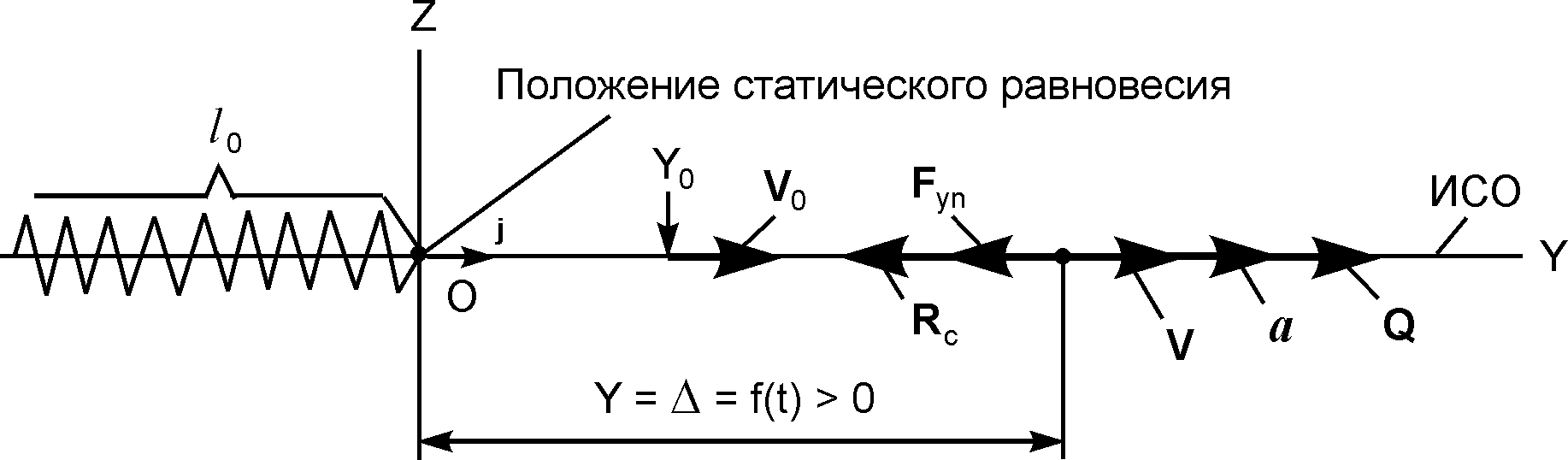

Начало системы отсчёта ОY поместим в положение статического равновесия материальной точки, при котором пружина не деформирована.

Основное уравнение динамики точки для рассматриваемого случая имеет вид

m·a = ΣF_i^E + ΣR_i^E = G + Q + R_c + N + F_yn.

Необходимо отметить, что силы G, Q являются активными силами, а силы R_c, N, F_yn отнесены к разряду реакций связей. Так как силы G и N не влияют на горизонтальное движение точки, то они на рис. 2.15 не показаны.

Из предыдущего материала, изложенного в данном разделе учебно-методического пособия, известно:

R_c = – α·V; F_yn = c·Δ; Q = H·sin(p·t + δ).

С учётом этого дифференциальное уравнение горизонтального движения точки описывается равенством

m· = Σ + Σ = H·sin(p·t + δ) – α· – c·Y.

Перенеся члены α· , c·Y в левую часть равенства и разделив обе его части на массу m, получим

+ (α/m)· + (c/m)·Y = (H/m)·sin(p·t + δ),

где c/m = k² – квадрат циклической частоты свободных колебаний; α/2m = n – коэффициент затухания; H/m = h – отношение амплитуды возмущающей силы к массе точки.

При этих обозначениях дифференциальное уравнение движения точки имеет вид

+ 2n· + k²·Y = h·sin(p·t + δ).

Последнее уравнение представляет собой дифференциальное уравнение вынужденных колебаний точки при наличии сопротивления движению, пропорционального скорости.

Общее решение этого уравнения состоит из общего решения Y^* дифференциального уравнения + 2n· + k²·Y = 0 и частного решения Y^**.

Таким образом, общее решение дифференциального уравнения + 2n· + k²·Y = h·sin(p·t + δ) имеет вид Y = Y^*+ Y^**.

Частное решение Y^** выражается формулой

Y^** = A_c·sin(p·t + δ – ε),

где А_с, ε – постоянные величины, не зависящие от начальных условий движения точки.

Эти постоянные называют: А_с – амплитуда вынужденных колебаний при наличии сопротивления движению; ε – сдвиг фазы.

Значения А_с и ε определяют по следующей совокупности формул:

A_c = h/( ); tg(ε) = 2·n·p/(k² – p²);

sin(ε) = 2·n·p·A_c/h; cos(ε) = A_c·(k² – p²)/h.

Общее решение дифференциального уравнения + 2n· + k²·Y = h·sin(p·t + δ)) в зависимости от соотношения величин k и n имеет вид:

при n < k Y = a·(e^-nt)·sin(k^*·t + β) + A_c·sin(p·t + δ – ε);

при n = k Y = (e^-nt)·(C₁·t + C₂) + A_c·sin(p·t + δ – ε);

при n > k Y = (e^-nt)·(C₁· ^)·t + C₂· ^)·t) +

+ A_c·sin(p·t + δ – ε),

где α, β, С₁, С₂ – постоянные интегрирования, определяемые по начальным условиям движения точки.

Н

Рис. 2.16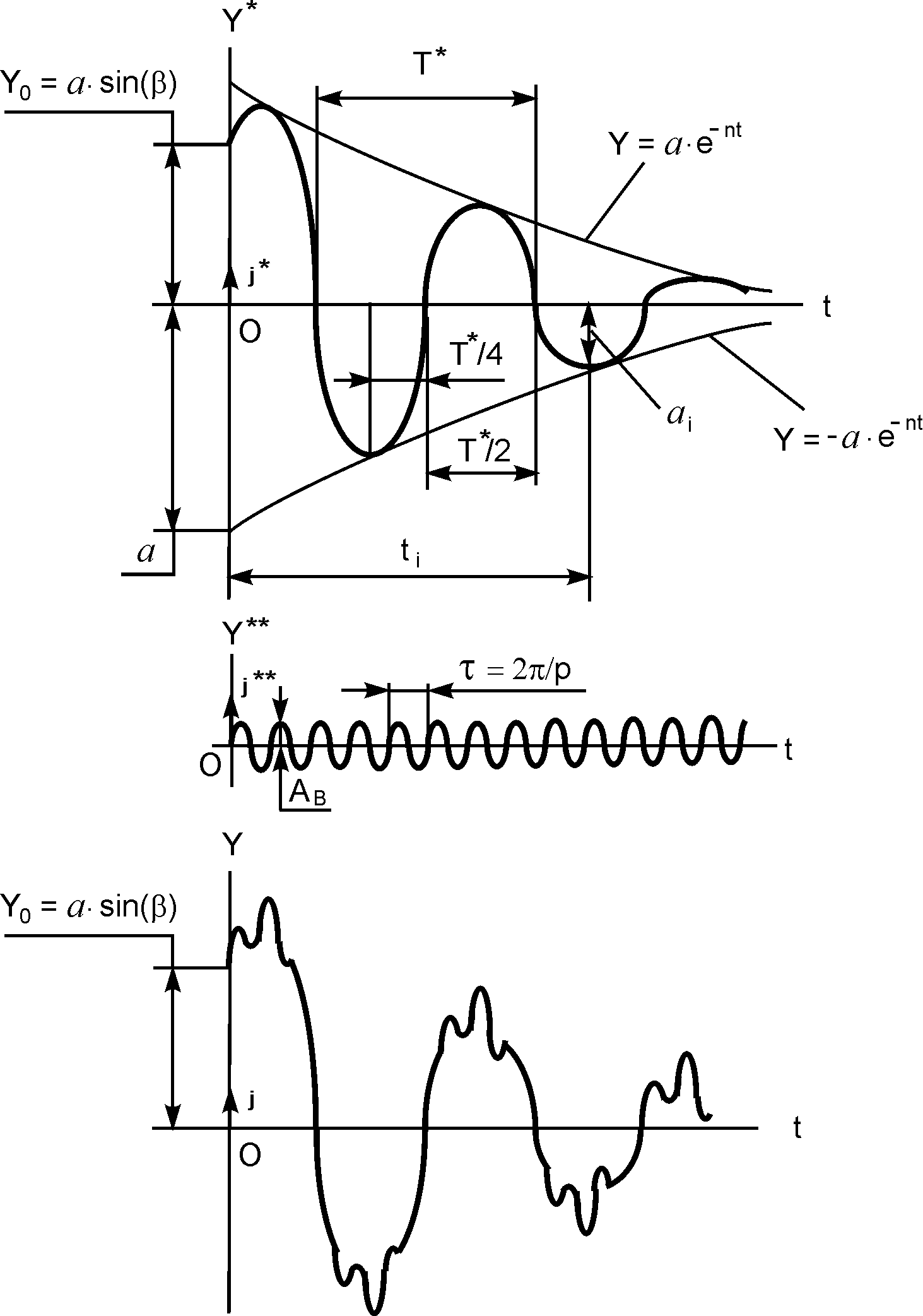

а рис. 2.16 приведены графики зависимостей: Y^* = f₁(t); Y^** = f₂(t); Y = f₃(t) для случая, когда n < k; p > k, и начальных условий Y₀ > 0, > 0.

Н

Рис. 2.17

а рис. 2.17 приведены графики зависимостей Y^* = f₁(t), Y^** = f₂(t), Y = f₃(t) для случая, когда n = k; p > k, и начальных условий Y₀ > 0; >0.

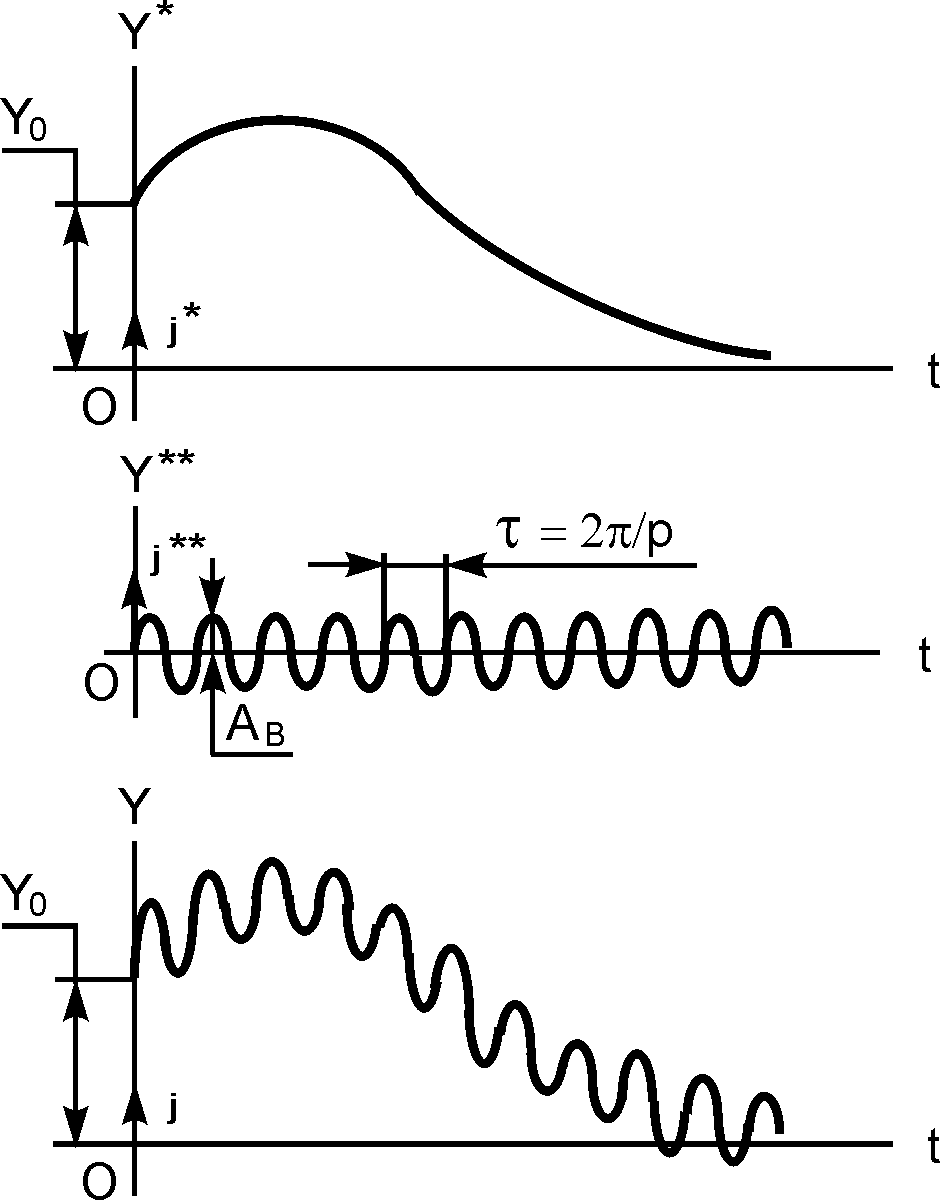
Таким образом, графики зависимостей Y = f₃(t) на рис. 2.16, 2.17 при p > k представляют собой наложение высокочастотных вынужденных колебаний Y^** = f₂(t) соответственно на затухающие колебания (см. рис. 2.16) или апериодическое движение (см. рис. 2.17).