Варианты 26 – 30 (рис. 1.14)

И

Рис. 1.14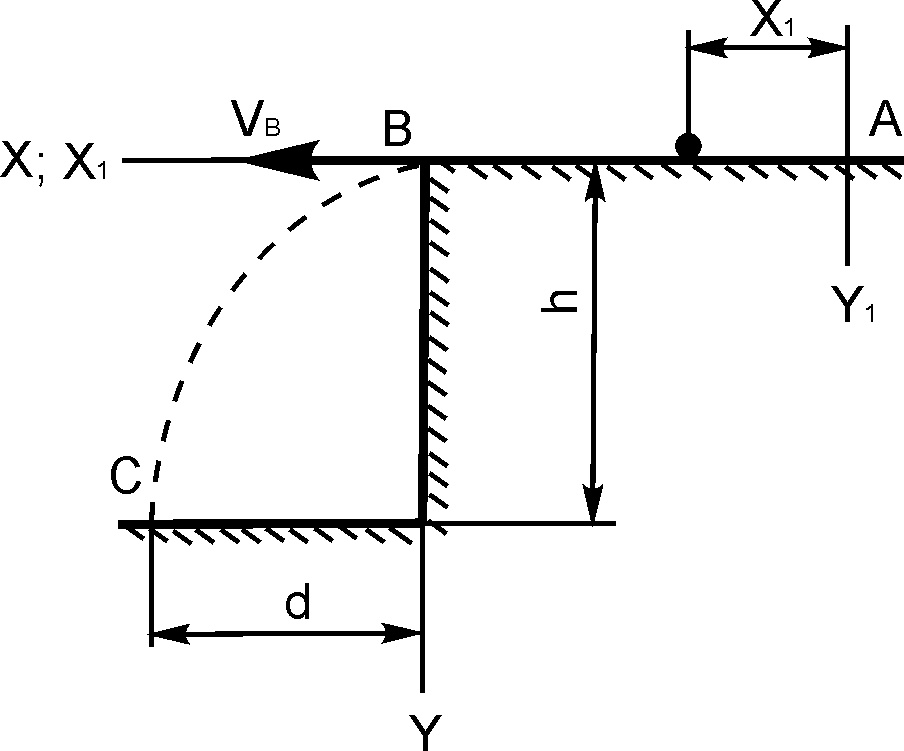

мея в точке А скорость V_A, тело движется по горизонтальному участку АВ длиной l в течение τ секунд. Коэффициент трения скольжения по плоскости равен f. Со скоростью V_B тело в точке В покидает плоскость и попадает в точку С со скоростью V_C, находясь в воздухе Т секунд.

При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.

Вариант 26. Дано: V_A = 7 м/с; f = 0,2; l = 8 м; h = 20 м. Определить V_C и d.

Вариант 27. Дано: V_A = 4 м/с; f = 0,1; τ = 2 c; d = 2 м. Определить V_B и h.

Вариант 28. Дано: V_B = 3 м/с; f = 0,3; l = 3 м; h = 5 м. Определить V_A и Т.

Вариант 29. Дано: V_A = 3 м/с; V_B = 1 м/с; l = 2,5 м; h = 20 м. Определить f и d.

Вариант 30. Дано: f = 0,25; l = 4 м; d = 3 м; h = 5 м. Определить V_A и τ.

1.13. Пример выполнения курсового задания д 1

В общем случае система сил, действующая на материальную точку, может быть постоянной или зависеть от времени t, положения в пространстве, скорости и т. д. В связи с этим интегрирование дифференциальных уравнений движения точки имеет свою специфику. В курсовом задании Д 1 система сил, действующая на точку, постоянна. Рассмотрим пример выполнения этого задания.

Условие задания.

Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом. Его начальная скорость V_A. Коэффициент трения скольжения равен f. Через τ секунд тело в точке В со скоростью V_B покидает наклонную плоскость и падает на горизонтальную плоскость в точку С со скоростью V_C; при этом оно находится в воздухе Т секунд (рис. 1.15).

При решении задачи принять тело за материальную точку и не учитывать сопротивление воздуха.

Д

Рис. 1.15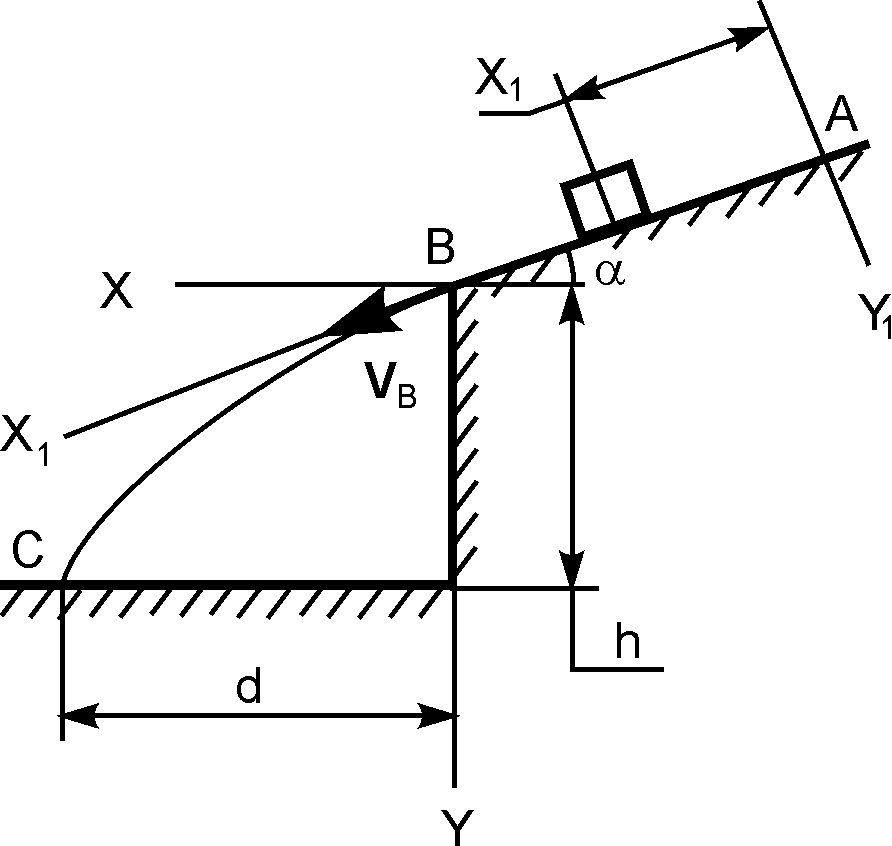

ано: V_A = 1 м/с; α = 30^о; f = 0,2; l = 6 м; h = 4,5 м. Определить V_C и τ.

Решение.

1

Рис. 1.16

. Рассмотрим движение тела на участке АВ в заданной системе отсчёта АX₁Y₁, приняв его за материальную точку (рис. 1.16).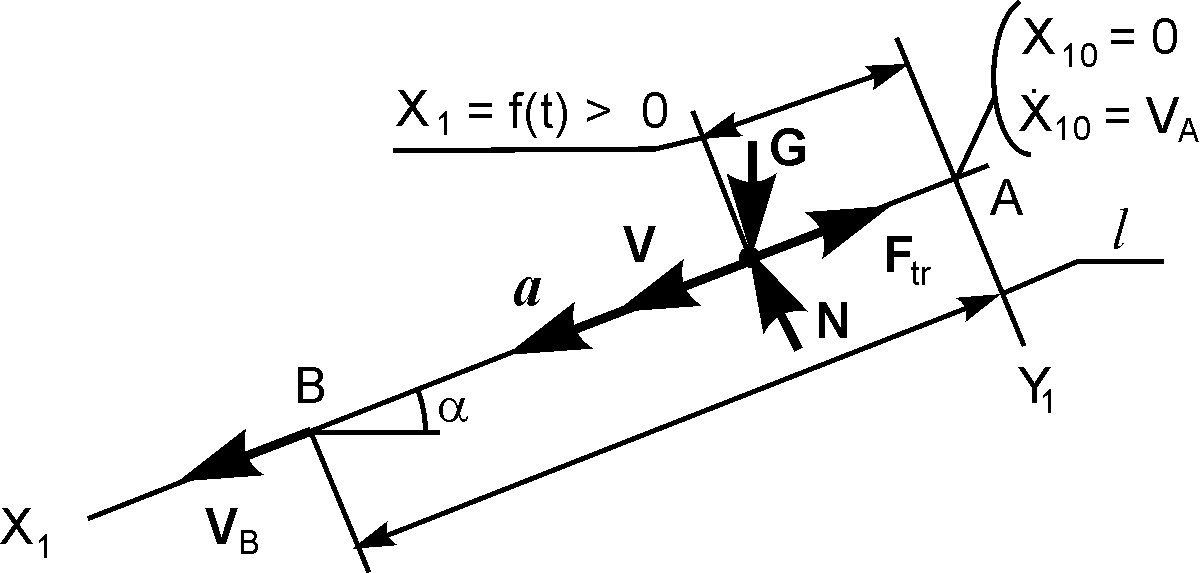

Такое допущение обосновано тем, что тело совершает поступательное движение и, следовательно, уравнения его движения такие же, как и у точки.

2. Изобразим точку в системе отсчёта АX₁Y₁ в произвольный момент времени t. При этом её координата Х₁ = f(t) > 0 и точка движется в сторону возрастания этой координаты ускоренно. Следовательно, ускорение a имеет такое же направление, как и скорость V.

3. Согласно условию задачи при t₀ = 0 начальная координата Х₁₀ = Х_1А = 0 и проекция начальной скорости = V_A.

4. К точке приложим активную силу G – силу тяжести. Так как опорная поверхность точки шероховатая, то имеем две реакции: N – нормальная реакция; F_tr – сила трения скольжения. Силу F_tr направляют в сторону, противоположную направлению скорости V. Из курса статики известно, что модули силы трения и нормальной реакции связывает соотношение F_tr = f·N.

5. Запишем основное уравнение динамики точки.

m·a = ΣF_i^Е + ΣR_i^Е = G + N + F_tr.

Спроецировав это векторное выражение на координатные оси системы отсчёта АX₁Y₁, получим дифференциальные уравнения движения точки:

m· = G·sin(α) – F_tr; (1)

m· = G·cos(α) – N, (2)

где , – проекции ускорения a на координатные оси.

Поскольку вектор a на ось AY₁ не проецируется, то из уравнения (2) имеем N = G·cos(α) = m·g·cos(α). Отсюда имеем

F_tr = f·N = f·m·g·cos(α).

Анализируя последнее равенство, сделаем вывод о том, что реакции N и F_tr не зависят от того, в каком кинематическом состоянии (покоя или движения) находится точка.

С учетом изложенного уравнение (1) приводится к виду

m· = G·sin(α) – F_tr = G·sin(α) – f·N·cos(α) =

= m·g·sin(α) – f·m·g·cos(α) = m·g·(sin(α) – f·cos(α)). (1^I)

Упростим последнее выражение.

= g·(sin(α) – f·cos(α)). (1^II)

6. Дважды проинтегрируем последнее уравнение.

= g·(sin(α) – f·cos(α))·t + C₁;

X₁ = g·(sin(α) – f·cos(α))·t²/2 + C₁·t + C₂,

где С₁, С₂ – постоянные интегрирования.

7. Определим постоянные С₁, С₂ подстановкой в последние уравнения начальных условий движения. При t₀ = 0 имеем:

= V_A = g·(sin(α) – f·cos(α))·t₀ + C₁;

X₁₀= Х_1A = 0 = g·(sin(α) – f·cos(α))·(t₀)²/2 + C₁·t₀ + C₂.

Отсюда С₁ = V_A; С₂ = 0. Окончательно имеем:

= g·(sin(α) – f·cos(α))·t + V_A;

X₁ = g·(sin(α) – f·cos(α))·t²/2 + V_A·t,

где X₁, – соответственно текущие координата точки и проекция её скорости на координатную ось АХ₁.

Последние выражения справедливы для любого значения времени, пока точка движется по участку АВ. В момент времени τ движущееся тело находится в точке В участка АВ. Исходя из этого, получим систему двух уравнений.

= V_B = g·(sin(α) – f·cos(α))·τ + V_A;

Х₁(τ) = l = g·(sin(α) – f·cos(α))·τ²/2 + V_A·τ.

Эта система уравнений содержит неизвестные τ и V_B. Поскольку число уравнений равно числу неизвестных величин, то такую систему уравнений решают стандартными приёмами и определяют V_B и τ. После определения V_B и τ рассматривают движение материальной точки на участке ВС её траектории в системе отсчёта ВХY (см. рис. 1.15).

Если последнюю систему уравнений решить нельзя (число неизвестных превышает число уравнений равновесия), то так же переходят к рассмотрению движения точки на участке ВС в системе отсчёта ВXY.

8. Рассмотрим движение точки на участке ВС в заданной системе отсчёта ВXY.

9

Рис. 1.17

. Изобразим точку на траектории её движения в произвольный момент времени (рис. 1.17).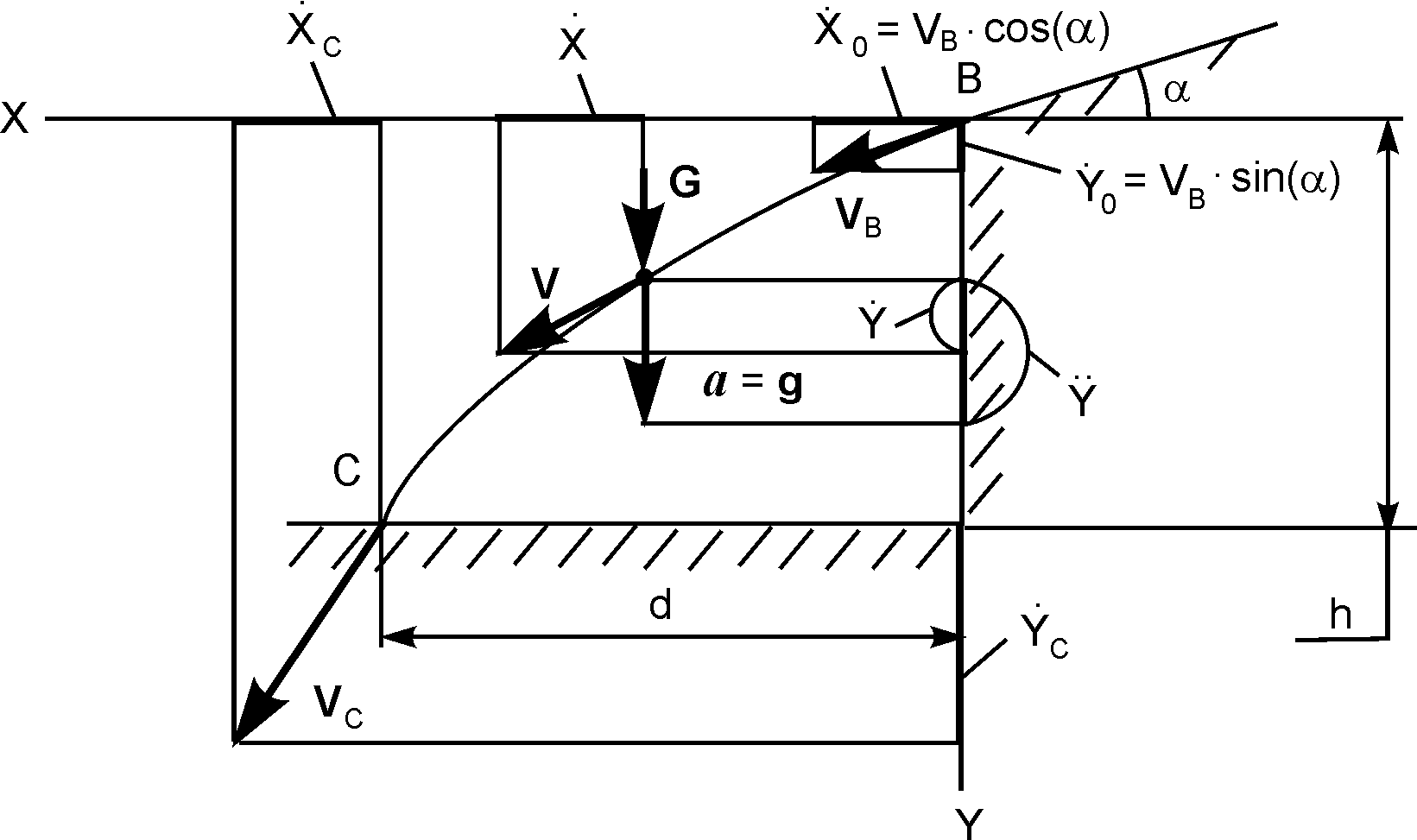

10. Определим начальные условия движения точки на участке ВС. Согласно рис. 1.17 имеем: Х₀ = 0; = V_B·cos(α); Y₀ = 0; = V_B·sin(α).

11. На точку действует только одна активная сила G – сила тяжести. Реакций связей нет, поскольку сопротивление воздуха не учитывается.

12. Основное уравнение динамики для точки имеет вид

m·a = ΣF_i^E + ΣR_i^E = G.

Запишем дифференциальные уравнения движения точки.

m· = Σ + Σ = 0; (3)

m· = Σ + Σ = G = m·g. (4)

13. Проинтегрируем последние уравнения. Так как масса точки m ≠ 0, то из уравнения (3) имеем = 0. Отсюда следует, что = C₃ = const, где – проекция скорости на координатную ось ВХ; С₃ – постоянная интегрирования. Определим С₃ по начальным условиям движения. При t₀ = 0 имеем = V_B·cos(α) = C₃. Так как = const, то окончательно получим выражение = V_B·cos(α). Другими словами, в любой момент времени проекция скорости на координатную ось ВХ постоянна, т. е. не зависит от времени.

Проинтегрировав последнее выражение, получим

X = V_B·cos(α)·t + C₄,

где С₄ – постоянная интегрирования.

Определим эту постоянную по начальным условиям движения. При t₀ = 0 имеем X₀ = 0 = V_B·cos(α)·t₀ + C₄. Отсюда получим С₄ = 0. Окончательно текущее значение координаты X точки находят по формуле

X = V_B·cos(α)·t.

Дифференциальное уравнение (4) движения точки приведем к виду = g. Проинтегрируем это выражение и получим

= g·t + C₅,

где – текущее значение проекции скорости на координатную ось BY; С₅ – постоянная интегрирования.

По начальным условиям движения имеем

= V_B·sin(α) = g·t₀ + C₅.

Отсюда С₅ = V_B·sin(α). Тогда = g·t + V_B·sin(α).

Проведём интегрирование последнего выражения.

Y = g·t²/2 + V_B·sin(α)·t + C₆.

Определим постоянную интегрирования С₆. При t₀ = 0 имеем

Y₀ = 0 = g·(t₀)²/2 + V_B·sin(α)·t₀ + C₆.

Тогда С₆ = 0.

Текущее значение координаты y находят по формуле

Y = g·t²/2 + V_B·sin(α)·t.

Таким образом, получаем выражения для определения текущих значений координат X, Y и проекций , скорости точки при её движении по траектории ВС. В момент времени Т, когда тело находится в точке С траектории его движения (см. рис. 1.17), эти выражения приобретают следующий вид:

= V_B·cos(α); = g·Т + V_B·sin(α);

d = V_B·cos(α)·T; h = g·T²/2 + V_B·sin(α)·T,

где , – проекции скорости V_C на координатные оси; d, h – координаты точки С в системе отсчёта ВXY.

По условию задачи требуется определить модуль скорости тела в точке С траектории его движения. Для этого используется формула .

Таким образом, для определения неизвестных величин необходимо совместно решить следующую систему уравнений:

V_B = g·(sin(α) – f·cos(α))·τ + V_A;

l = g·(sin(α) – f·cos(α))·τ²/2 + V_A τ;

= V_B·cos(α);

= g·Т + V_B·sin(α);

d = V_B·cos(α)·T;

h = g·T²/2 + V_B·sin(α)·T;

.

В этой системе уравнений неизвестными величинами являются: V_B, τ, d, T, , , V_C.

Таким образом, имеем семь уравнений, содержащих семь неизвестных.

Для координации вектора V_C скорости тела в точке С пространства рекомендуется определить величину угла β, составленного направлением этой скорости с положительным направлением отсчета координаты Х по формулам:

cos(V_C, i) = /V_C; β = arcos( /V_C).

Результаты проведённых расчётов сводят в таблицу.