
- •Часть 1
- •Тема I множества и операции над ними. Отношения
- •Множества. Равенство множеств
- •Алгебра множеств
- •Декартово произведение и отношения
- •Эквивалентность
- •Частичный порядок
- •Тема II логика высказываний
- •2.1. Высказывания и операции над ними
- •2.2. Анализ сложного высказывания
- •2.3. Формулы. Булевы функции
- •2.4.Тавтологии
- •2.5. Построение контрпримера
- •2.6. Равносильные формулы
- •2.7. Некоторые логические законы
- •2.8. Нормальные формы
- •Тема III применение логики высказываний
- •3.1. Логическое следствие
- •3.2. Применение к переключательным схемам
- •Тема IV исчисление высказываний
- •Теория l. Аксиомы и правила вывода
- •Общезначимость теорем. Непротиворечивость l
- •Полнота теории l
- •Тема V алгебра предикатов. Понятие об исчислении предикатов
- •5.1. Понятие предиката.
- •5.2.Типы предикатов.
- •5.3. Простейшие логические операции над предикатами.
- •5.4. Операции квантификации.
- •5.5. Предикатные формулы.
- •5.6. Язык алгебры предикатов.
- •5.7. Понятие об исчислении предикатов.
- •Часть 2
- •I. Формулы, истинностные таблицы, нормальные формы
- •II. Построение формул по таблицам значений
- •III. Логические следствия, непротиворечивость суждений
- •IV.Некоторые задачи
- •Индивидуальные задания №3 предикаты
- •I. Множества истинности предикатов
- •II. Квантификация
- •III. Применение кванторов
- •IV. Тавтологии, предваренная форма
- •V. Решить задачу
- •Дополнительные вопросы
- •Литература
2.2. Анализ сложного высказывания
Если А и В высказывания, означающие
соответственно «![]() »
и «2 - простое число», то формула
»
и «2 - простое число», то формула
![]() представляет сложное высказывание
«если неверно, что
или 2 – простое число, то
и неверно, что 2 – простое число». Сложное
высказывание считается заданным тогда
и только тогда, когда оно допускает
единственный анализ, т.е.
однозначно определена последовательность
его получения из простых высказываний
с помощью пропозициональных связок.
Так, для рассматриваемого высказывания
эта последовательность будет следующей:
представляет сложное высказывание
«если неверно, что
или 2 – простое число, то
и неверно, что 2 – простое число». Сложное
высказывание считается заданным тогда
и только тогда, когда оно допускает
единственный анализ, т.е.
однозначно определена последовательность
его получения из простых высказываний
с помощью пропозициональных связок.
Так, для рассматриваемого высказывания
эта последовательность будет следующей:
|
|
1 1 1 1 2 2
3 3
4 |
определяем истинностные значения А и В; определяем истинностные значения и ;
определяем истинностные значения
определяем истинностное значение . |
Очередность выполнения операций при
формальной записи определяется скобками.
Во избежание нагромождения скобок в
логике, как и в арифметике, принято
соглашение о порядке действий, при
котором при отсутствии скобок логические
операции выполняются в следующем
порядке:
.
Так, рассматриваемая формула может быть
записана в виде
![]() .
.
Пример 1. Высказывание «неверно,
что хотя бы одно из чисел 19, 21, 36 является
квадратом натурального числа» расчленим
на простые и запишем, используя операции
над высказываниями. Обозначим А =
«число 19 является квадратом натурального
числа», В = «число 21 является квадратом
натурального числа», С= «число 36
является квадратом натурального числа»,
тогда высказывание
![]() можно прочитать: «хотя бы одно из чисел
19, 21, 36 является квадратом натурального
числа». А исходное высказывание можно
записать скудеющим образом:
можно прочитать: «хотя бы одно из чисел
19, 21, 36 является квадратом натурального
числа». А исходное высказывание можно
записать скудеющим образом:
![]() .
Заметим, что высказывания А, В
– ложны, высказывание С – истинно,
высказывание
– истинно, а исходное высказывание
– ложно.
.
Заметим, что высказывания А, В
– ложны, высказывание С – истинно,
высказывание
– истинно, а исходное высказывание
– ложно.
Пример 2. Формула
![]() анализируется следующим образом:
анализируется следующим образом:
|
|
1 1 1 1 1 1 2 2 2
3 3
4 |
определяем истинностные значения А, В, С;
определяем истинностные значения
и
определяем истинностные значения
определяем истинностное значение . |
Истинностные таблицы для пропозициональных связок позволяют по известным истинностным значениям простых высказываний определять истинностное значение любого сложного высказывания.
Пример 3.
|
|
л и л и и л л л и |
и и и л и л и и и и и и |
Контрольные вопросы и упражнения
Какие из следующих предложений являются высказываниями:
а) Волга впадает в Азовское море;
б) студент математического факультета;
в)
![]() ;
;
г)
![]() ;
;
д)
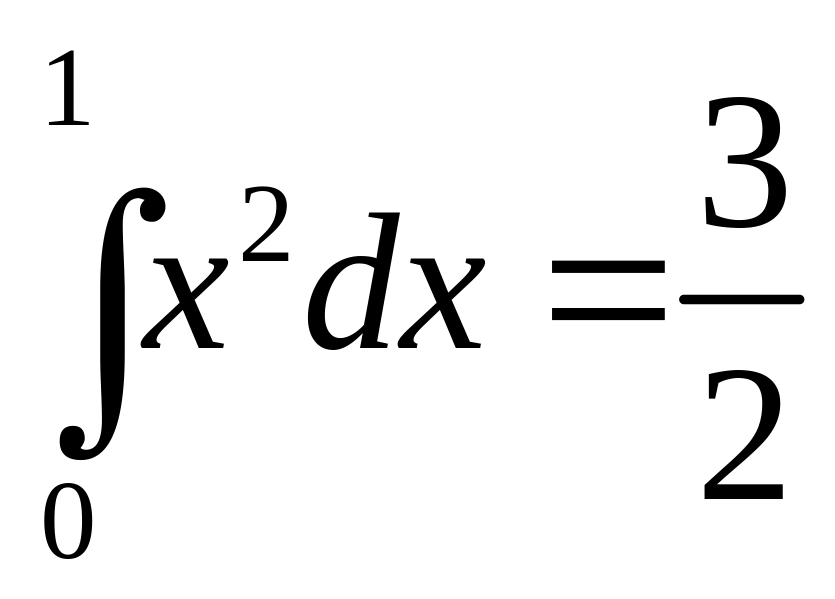 .
.
Пусть А – «сегодня ясно», В – «сегодня идет дождь», С – «сегодня идет снег», D – «вчера было пасмурно». Переведите на обычный язык следующие предложения:
а)
![]() ; в)
; в)
![]() ;
;
б)
![]() ; г)
; г)
![]() .
.
Следующие составные высказывания расчленить на простые и записать символически, введя сокращенные обозначения для простых их членов (т.е. для предложений, не содержащих связок, соответствующих логическим операциям):
а) идет дождь или кто-то не выключил душ;
б) если 18 делится на 2 и делится на 3, то оно делится на 6;
в) треугольник равносторонний тогда и только тогда, когда он равнобедренный;
г) неверно, что хотя бы одно из чисел 19, 21, 36 является квадратом натурального числа.
Пусть А = 1, В = 1, С = 0, D = 0. Найти истинностное значение каждого из высказываний:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
Пусть
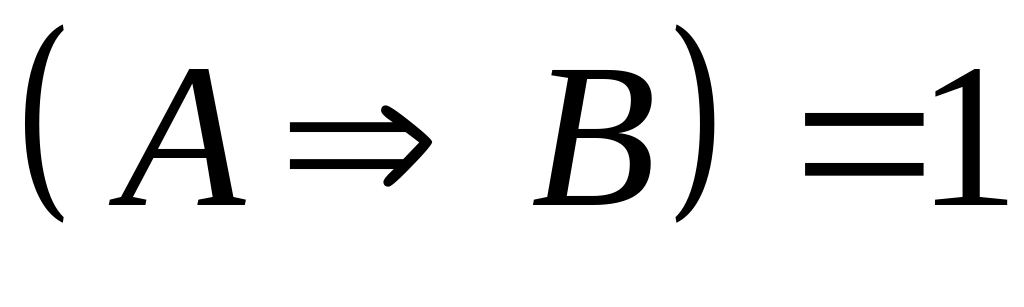 .
Что можно сказать о значении высказывания
.
Что можно сказать о значении высказывания
 ?
?Пусть
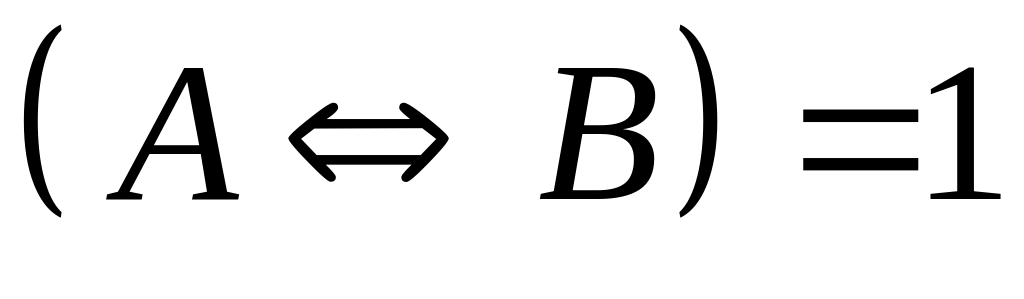 .
Что можно сказать о значениях высказываний
.
Что можно сказать о значениях высказываний
 и
и
 ?
?Сколько существует различных унарных и бинарных операций над высказываниями? Задать все эти операции с помощью таблиц.
Исключающей дизъюнкцией (или суммой по модулю 2) двух высказываний А и В называется высказывание
 (либо А, либо В), которое истинно,
когда одно, и только одно, из данных
высказываний истинно. Задать операцию
«+» таблицей и выразить ее через основные
операции над высказываниями.
(либо А, либо В), которое истинно,
когда одно, и только одно, из данных
высказываний истинно. Задать операцию
«+» таблицей и выразить ее через основные
операции над высказываниями.Логические операции «штрих Шеффера» (
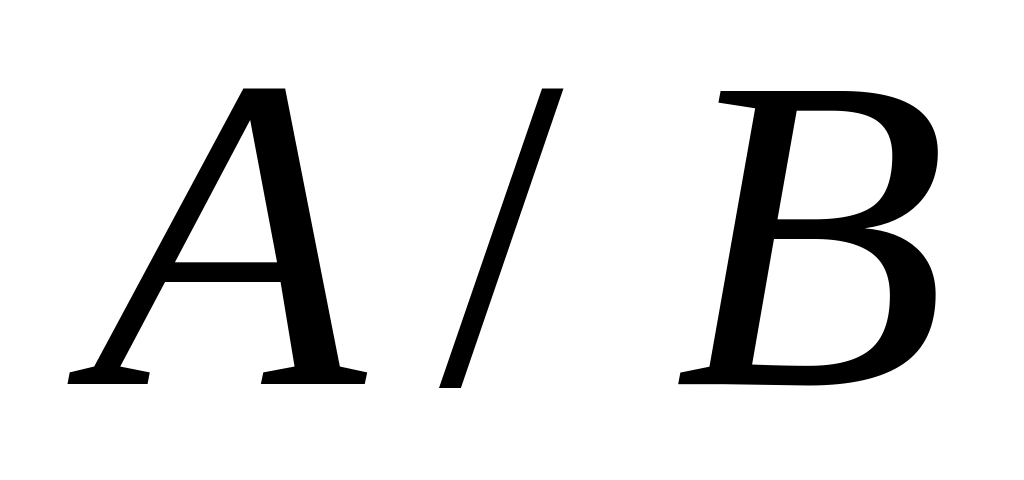 )
и «штрих Лукасевича» (
)
и «штрих Лукасевича» (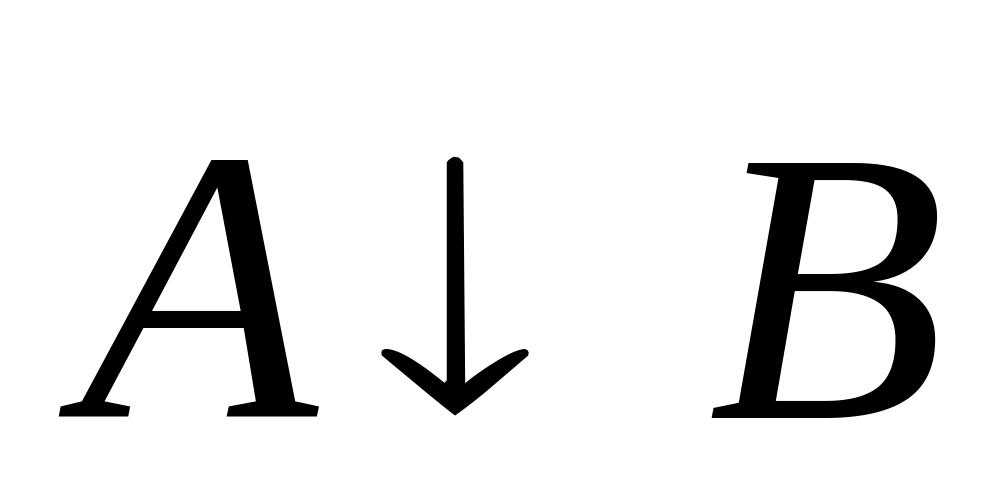 )
задаются таблицами:
)
задаются таблицами:
|
|
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
|
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Доказать, что все основные логические операции можно выразить только через штрих Шеффера либо только через штрих Лукасевича.
Доказать, что каждая тернарная логическая операция может быть выражена через основные бинарные.
