Masharov_KAN

ÓÄÊ 517.53 (075.8)

ÁÁÊ Â161.5ÿ73

Ì38

Укладач:

П. А. Машаров, канд. iз.-мат. наук, доц.

дповiдальний за випуск:

Âiт. В. Волчков,

- iз.-мат. наук, завiдувач ка едри математичного

аналiзу i ди еренцiальних рiвнянь, про .

ецензенти:

-ð

.- .

ïðî .

В. Волчков,

Â. I. Пайков, канд.

iç.-ìàò. íàóê, äîö.

Комплек

аналiз: посiбник / уклад. П. А. Машаров. Донецьк:

ДонНУ, 2013.

ñíèé80 .

осно нi теоретичнi вiдомостi, приклади розв'яз ння

Ïî iáíèê

типових задач мiститьдвадцять варiантiв завдань розрахункових робiт 1 та 2 з

омплексного а

àëiçó.

Для студе

тiв спецiальностей Математика , Статистика акультету

ÎÇÄIË 1

ЕЛЕМЕНТИ ДIЙСНО О АНАЛIЗУ

a

1.1 Многоч ени

=6 0 називають многочленом n-го степеня. Число називають нулем або

Функцiю виг яду P

n

(x) = a

n

xn + a

n 1

xn 1

+ : : : + a

2

x2 + a

x + a

, äå

кnренем многочлена P

1

0

n

(x), якщо це число ¹ розв'язком рiвняння P

n

(x) = 0,

òîáòî Pn( ) = 0.

÷ëåí

Якщо корiнь многочлена P (x), то iснують

fb gn 1 òàêi, ùî

Pn(x)

дiлиться

(x )

áåç

остчислачi,

випадкумногочлен

P

n

(x) = (x ) b

n 1

xn 1

+ b

n 2

xn 2

+n: : :+ b

x+ b

. У цьому

k

k=0

-

1

0

íà (x ). Ê å iöi¹íòè

многочлена Qn 1(x) можна обчислити за допомогою

Q

n 1

(x) = b

n 1

xn 1

+ b

n 2

xn 2

+ : : : + b x + b

0

¹ часткою вiд дiлення P

n

(x)

дiлення кутî÷êîì

бо за схемою о нера.

k 2 N многочлена P (x), якщо

Число називà¹ться коренем кð

ма¹ мiсце рiвнiсть P (x) = (x )kQ(xатностi), не ¹ коре

åì

Q(x).

óíêöi¨.

виду P (x) = 0 називають

âiäïîâiäíî äî òèïó óíêöi¨

Найпростiшими прикладами многочленiв ¹ лi iйнамногочленаквадратична

P (x). озв'язати лiнiйне рiвняння (ax + b = 0) досить

просто,

не будемо на

цьому зупинятисiвняння.

òà x

квадратичнî¨ óíêöi¨ ax2

+ bx + (a =6 0)

Знайти дiйснi коренi x

1

2

можна одним

наступних способiв.

дискримiнант

D = b2

1. Через

дискримiмнант. Для цього обчислюють

4a , i ÿêùî D > 0, òî x

1;2

=

b pD ; якщо D < 0, то дiйсних

коренiв нема¹.

2a

2. Ч рез поло инний дискримiмíàíò. Öåй метод використовують ко-

ли b парне,

тобто

к адратне рiвняння ма¹ âèãëÿä ax

2

+2kx+ = 0 (a =6 0).

Òîäi D1 = k2

a , i, âiäïîâiäíî, x1;2 =

k pD1 .

a

òà x

,

3. За теоремою Вi¹та. Якщо вдалось пiдiбрати д а числа x

1

äëÿ ÿêèõ x

x

= =a, x

+ x

2

1

2

1

2

= b=a, òî âîíè ¹ ðîçâ'язками рiвняння

ax

2

+ bx + = 0.

рiвняння в щого степеня використо

Для розв'язання алгебр

вують

ди розкладання

à¨чногом жники, з мiнè. Для розв'язкiв рiвнянь

третьогометоа четвертого степеíя iснують спецiàльнi ормули (Кардано, Фер-

ðàði).

6

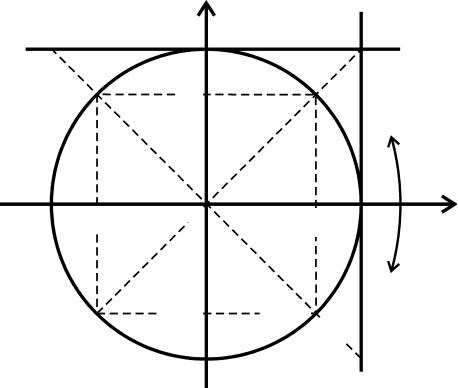
1.2 Тригонометрiя

чення тригонометричних ункцiй для

Вимiрювання кутiв,

кутiв наведено на рис. 5.1

визнат 1.2.

sin '

tg '

дiйсних значень аргумента, вiдомi точнi значення цих ункцiй для деякивсiх

У квадратних дужках

p3

пiдписи точок вiсей tg та tg,

в круглих точок кола.

p

3

p

3

p

p

3

3

1 [0

3

tg '

3

2

p3

3

5

3

2

2

p

1

( )

3

+'

6( )

2

6

(0) [0

1 p

3

1

0

1

p

3

1

p

'

os '

7

2

2

1

2

2

3

65

4

2

6

6

p3

3

3

2

2

2

Числа без дужок

1

3

3

3

2

пiдписують вiсi os та sin.

p

3

ис. 1.1 Значення

íîìåòðичних ункцiй кутiв, краòíèõ =6

Нагада¹мо деякi

тригономеòðè÷íi

ормули.

os

sin

2

2

tg =

sin

;

tg

;

+ os = 1;

os

sin

sin( )

os( )

os sin sin ;

sin os os sin ;

os

os2

1 + os

1

sin2

1 os

1

2

=

2

;

se =

os

2

=

2

; ose =

sin

:

sin '

tg '

[ 1

1 [0

[1

tg '

p

2

3

2

4

2

4

+'

( ) ( )

2

2

(0) [0

1

p

0

p

1

(2 )

os '

5

2

p

2

2

7

'

3

4

2

4

4

4

1

2

[ 1

3

ис. 1.2 Значення тригонометричних2 ункцiй кутiв, кратних =4

Ñóòü îðìóë зведення мiститься

наст пному. Нехай f одна з три-

óíêöié, g âiäìiííà âiä f

ó

äîâiëüíié ç ïàð (sin; os) àáî

ãîíîметричнихtg). Т дi f(k +

= çíàê

h( ), де знак вiдповiда¹ знаку ункцi¨

f

k

+ ") для " 2 2(0; =2), а в якостi ункцi¨ h обира¹мо f якщо k парне,

2

(tg;i якщо k непарне.

та гiперболiчнi ункцi¨

1.3 Показник

Пригада¹мо,

овадiйсному аналiзi вводяться поняття кореня та степе

ня. Ари метичним к

n-того степеня (n 2 N, n > 1) з

числа a

як оренемак невiд'¹мне число b, що b

= a. В дiйсному аналi-

степеня (2назива¹тьсn 1) вiд'¹много числа a назива¹ться таке вiд'¹мненевiд'¹многочисло b, щ

n

непарного

зi кореня парного степеня з вiд'¹много числа не iсну¹. Коре

b

2n 1

= a.

овим показником

Äëÿ âñiõ a > 0 ñòåïiíü ç ðàöiîíальним нену

водитьсÿ за ормулою a

=

a

. Äëÿ

довiльного

a =6 0 покладають

m=n

p

m

a0

= 1. Âèðàçó 00

n

не надають

. Якщо a < 0, то, хоча для непарногоm=n

p

n

rn

виразó am=n íå iñíó¹.

a цiлком визна

сенсудiйсному аналiзi вважа¹ться, що значення

Якщо тепер a > 0, чений,2 R то за визначенням покладають a

= lim a .

!

rn2Q

âîñòi Нагада¹моäié çi степеняàêîæìè: визначення ãiïåðáîëi÷íèõ óíêöié òà äåÿêi âëàñòè-

ex

+ e x

ex e x

sh x

h =

2

sh x

2

;

th x

;

th

sh x;

h2 x sh2 x = 1;

ax+y = ax ay;

ax

y = axy;

a x =

1=ax:

еомет

iÿ

ямокутна система координат (ДСК)

1.4.1 Декартова або

Проведемо на площинi чепрез точку O двi вза¹мно перпендикулярнi пря-

мi x y вiсi координат. Вiсь x (вона зазвичай горизонт

початком координат. На вiсях координат

ями направоальна)т вгору вв

ють додатними, позначаючи

¨х стрiлками,

отилежнi вiд'¹мними.назива¹тьсÍ êî-

вiссю абсцис,

вiсь y (вертикальна) вiссю орд

íàò. Òî÷ê O

ÿ

ординатн х вiсях позначають одиничнi вiднапрiзки, за допомог ю яких можна

визначити

координати точок на вiсях. Кожнiй точцi A на площинi ставлять

у вi повiднiсть пару чисел

оординати точки. Цi координати (абсцису (x)

i îðäинату (y)) знах дять як проекцi¨

A

âiäïовiднi координатнi вiсi.

Якщо точки A i B у ДСК мають

рдинати A(x1; y1), B(x2; y2), то вiд

стань мiж ними обчèñëþ¹òüñÿ çà

точкил ю jABj = p(x x )2 + (y y )2.

Òî÷ê C, ùî äiëèть вiдрiзок AB ормувi ношеннi

AC : CB = m : n, ì๠êîîð-

динати C

nx1+mx2

; ny1

+my2 .

2

1

2

1

m+n

m+n

1.4.2 Полярна система координат (ПСК)

м, який називають ну

Полярна с стема координат

ÿ

льовим або п лярною вiссю. Точка,зада¹тьсяко¨ вихпромендить цей

промiнь, назива¹ться

ом координат

або полюсом. Будь-як

iíøà

на площинi визна-

початкординатдвома(зазвичай познача¹ться r або )