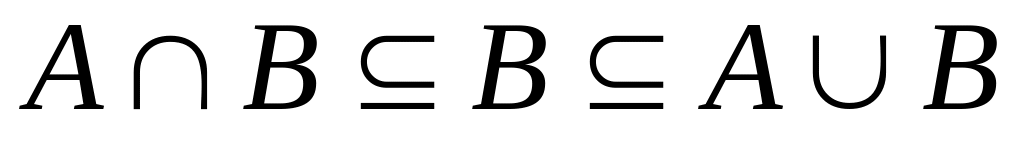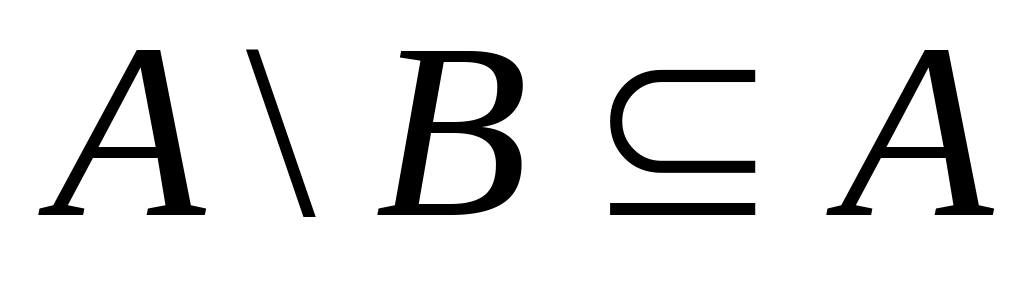- •Часть 1
- •Тема I множества и операции над ними. Отношения
- •Множества. Равенство множеств
- •Алгебра множеств
- •Декартово произведение и отношения
- •Эквивалентность
- •Частичный порядок
- •Тема II логика высказываний
- •2.1. Высказывания и операции над ними
- •2.2. Анализ сложного высказывания
- •2.3. Формулы. Булевы функции
- •2.4.Тавтологии
- •2.5. Построение контрпримера
- •2.6. Равносильные формулы
- •2.7. Некоторые логические законы
- •2.8. Нормальные формы
- •Тема III применение логики высказываний
- •3.1. Логическое следствие
- •3.2. Применение к переключательным схемам
- •Тема IV исчисление высказываний
- •Теория l. Аксиомы и правила вывода
- •Общезначимость теорем. Непротиворечивость l
- •Полнота теории l
- •Тема V алгебра предикатов. Понятие об исчислении предикатов
- •5.1. Понятие предиката.
- •5.2.Типы предикатов.
- •5.3. Простейшие логические операции над предикатами.
- •5.4. Операции квантификации.
- •5.5. Предикатные формулы.
- •5.6. Язык алгебры предикатов.
- •5.7. Понятие об исчислении предикатов.
- •Часть 2
- •I. Формулы, истинностные таблицы, нормальные формы
- •II. Построение формул по таблицам значений
- •III. Логические следствия, непротиворечивость суждений
- •IV.Некоторые задачи
- •Индивидуальные задания №3 предикаты
- •I. Множества истинности предикатов
- •II. Квантификация
- •III. Применение кванторов
- •IV. Тавтологии, предваренная форма
- •V. Решить задачу
- •Дополнительные вопросы
- •Литература
Эквивалентность
Двуместное однородное отношение на множестве А называется эквивалентностью, если - одновременно рефлексивно, симметрично и транзитивно.
Примеры эквивалентностей.
Отношение равенства для чисел.
Отношение подобия фигур (каждая фигура подобна себе – рефлективность, всегда, если фигура α подобна фигуре β, то и фигура β подобна α – симметричность; всегда, если фигура α подобна фигуре β, а фигура β подобна фигуре γ, то фигура α подобна фигуре γ - транзитивность).
Отношение параллельности прямых, лежащих в одной плоскости (каждая прямая
 параллельна себе – рефлективность,
для любых прямых
параллельна себе – рефлективность,
для любых прямых
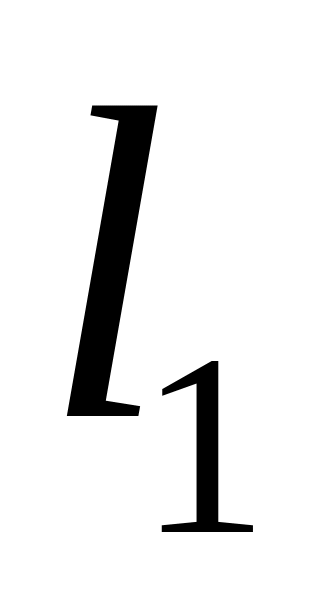 и
и
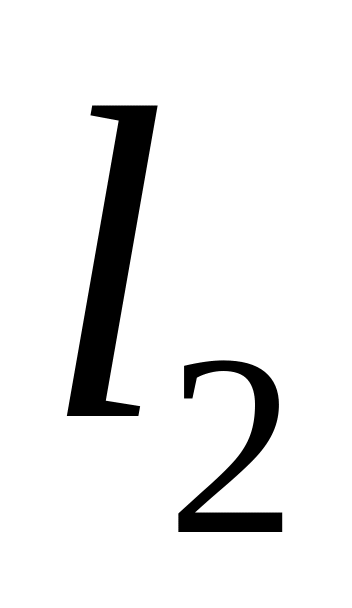 ,
если
,
если
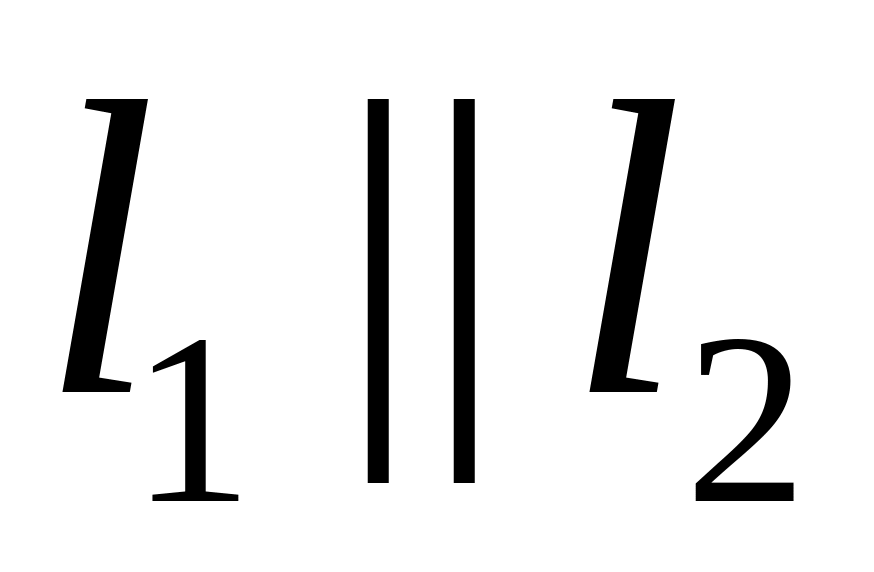 ,
то и
,
то и
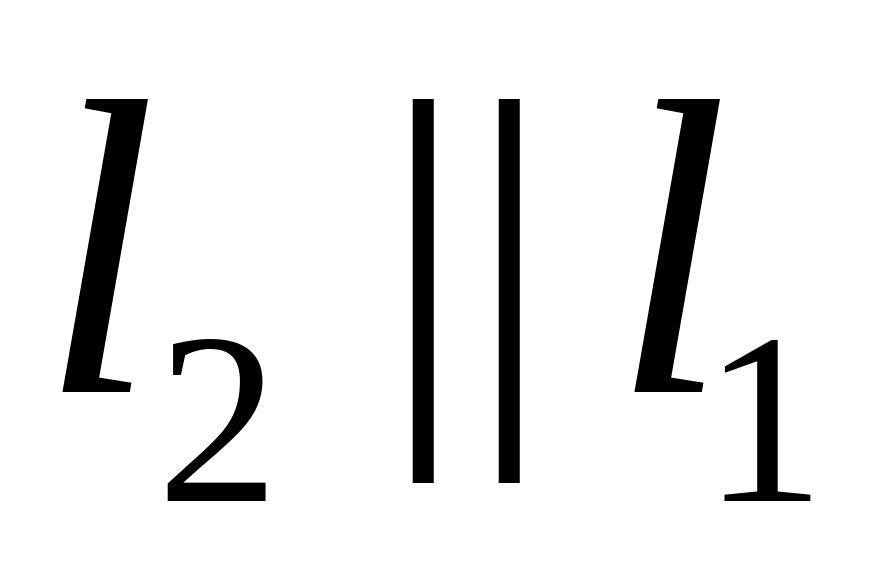 - симметричность, для любых прямых
,
и
- симметричность, для любых прямых
,
и
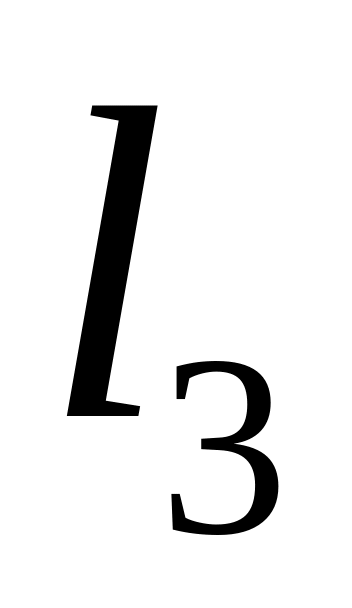 ,
если
и
,
если
и
 ,
то
,
то
 - транзитивность).
- транзитивность).
Говорят, что
![]() является разбиением множества
А, если
является разбиением множества
А, если
![]() и
и
![]() ,
если
,
если
![]() .
.
Пусть
- эквивалентность на А и
![]() ,
тогда множество
,
тогда множество
![]() называется классом эквивалентности,
порожденным элементом а, и обозначается
через
называется классом эквивалентности,
порожденным элементом а, и обозначается
через
![]() .
.
Подчеркнем, что
![]() .
.
Классы эквивалентности обладают свойствами:
а)
![]() ;
;
б) если
![]() ,
то
,
то
![]() ;
;
в) если
![]() ,
то
,
то
![]() .
.
Доказательство этих свойств дано в [1], с. 44-45.
Теорема. Если
- эквивалентность на А, то система
классов эквивалентности
![]() задает разбиение множества А.
Наоборот, если
- разбиение множества А, то определим
следующее двуместное отношение
задает разбиение множества А.
Наоборот, если
- разбиение множества А, то определим
следующее двуместное отношение
![]() на А:
на А:
![]() для некоторого
для некоторого
![]() .
Тогда
является эквивалентностью на А.
.
Тогда
является эквивалентностью на А.
Доказательство этой теоремы можно найти в [1], с. 45.
Отметим, что данная теорема позволяет
строить различные эквивалентности на
одном и том же множестве А. например,
пусть
![]() .
Зададим его разбиение
.
Зададим его разбиение
![]() ,
тогда получим на А следующую
эквивалентность
,
тогда получим на А следующую
эквивалентность
![]() .
Разбиению же
.
Разбиению же
![]() соответствует эквивалентность
соответствует эквивалентность
![]()
![]() .
Эквивалентность
.
Эквивалентность
![]() имеет следующие классы эквивалентности:
имеет следующие классы эквивалентности:
![]() ,
,
![]() ,
которые задают разбиение множества
,
которые задают разбиение множества
![]() .
.
Частичный порядок
Отношение на множестве А называется частичным порядком на А, если оно рефлексивно, транзитивно и антисимметрично.
Частичный порядок
на А
называется линейным
порядком на А,
если для любых
![]() выполняется хотя бы одно из следующих
двух условий:
,
выполняется хотя бы одно из следующих
двух условий:
,
![]() .
.
Примеры частичных порядков.
Отношение равенства для чисел.
На множестве
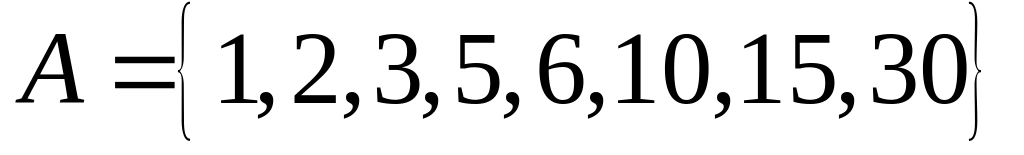 рассмотрим отношение
рассмотрим отношение

 и
и
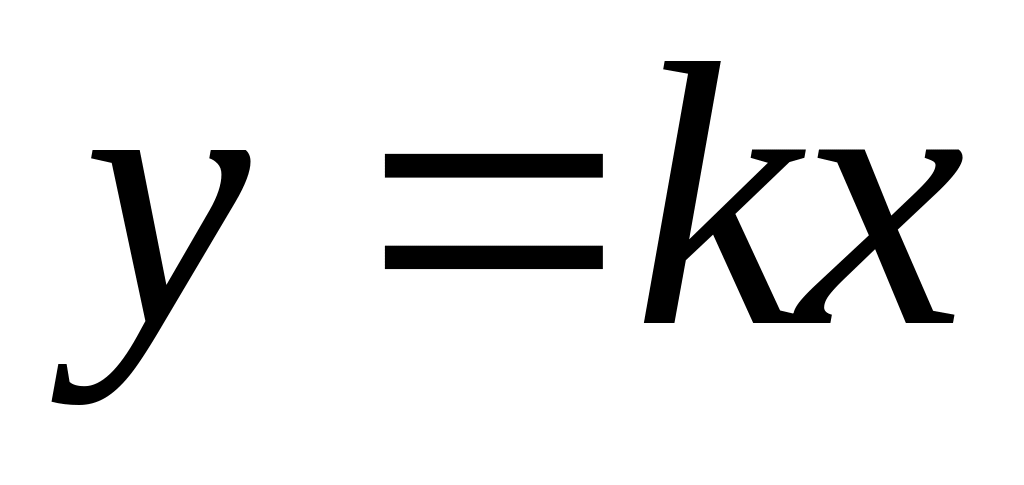 ,
где
,
где
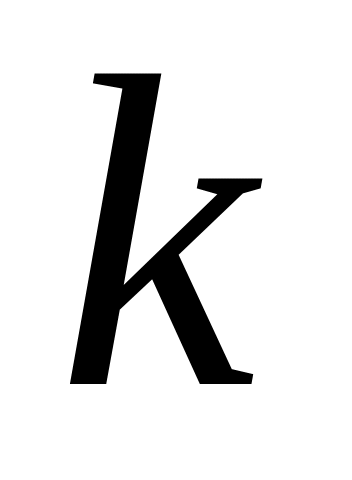 - некоторое натуральное число}. Так как
для любого
- некоторое натуральное число}. Так как
для любого
 ,
то
является рефлексивным. Пара
,
то
является рефлексивным. Пара
 тогда и только тогда, когда
тогда и только тогда, когда
 (т.е.
)
и
(т.е.
)
и
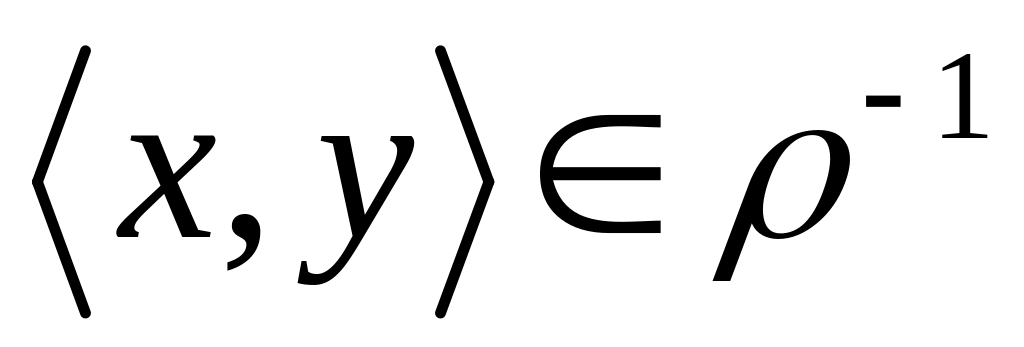 (т.е.
(т.е.
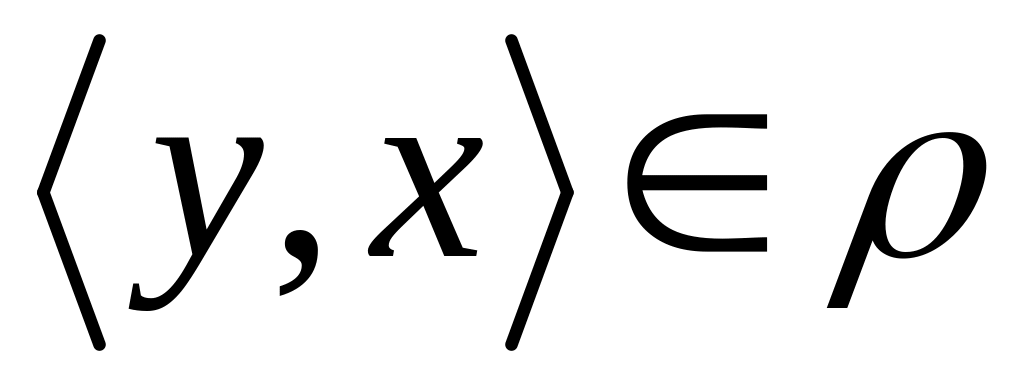 или
или
 ),
следовательно,
),
следовательно,
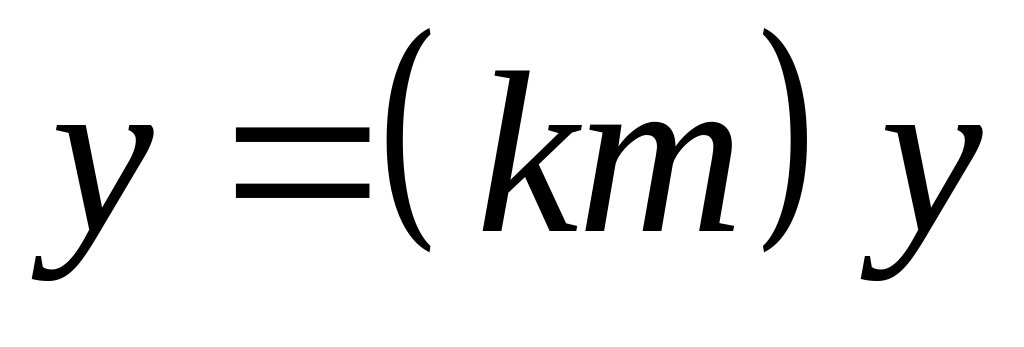 ,
откуда
,
откуда
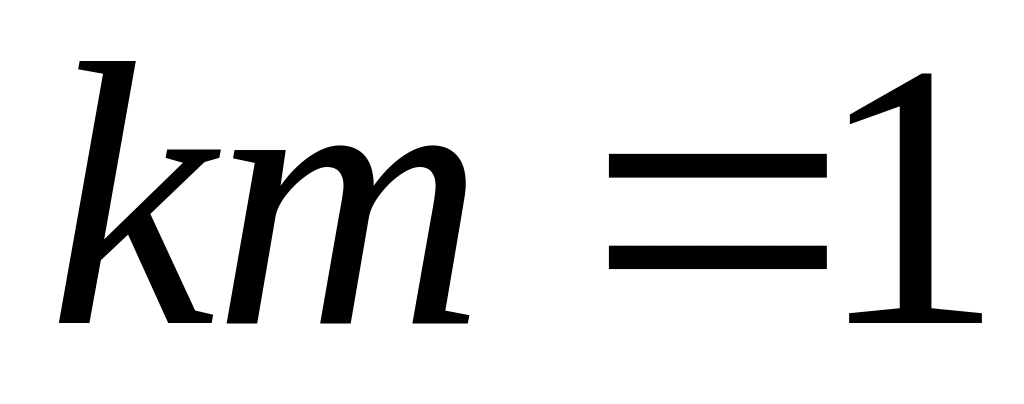 и
и
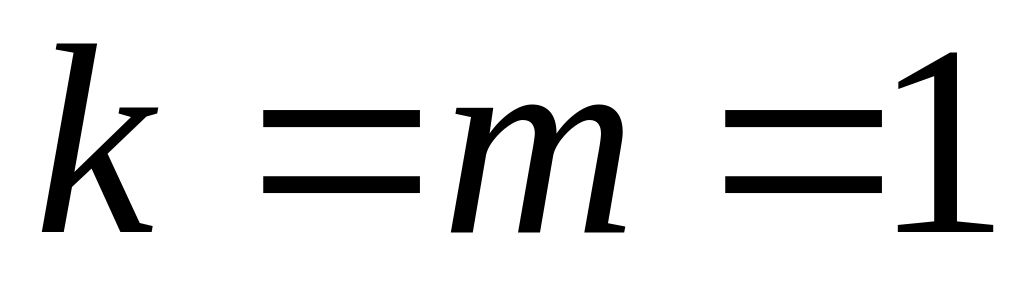 ,
что и означает антисимметричность
.
Если
(т.е.
)
и
,
что и означает антисимметричность
.
Если
(т.е.
)
и
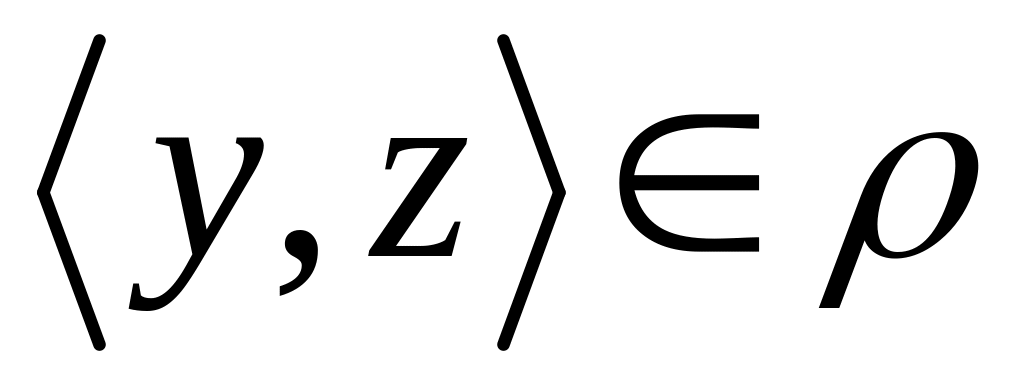 (т.е.
(т.е.
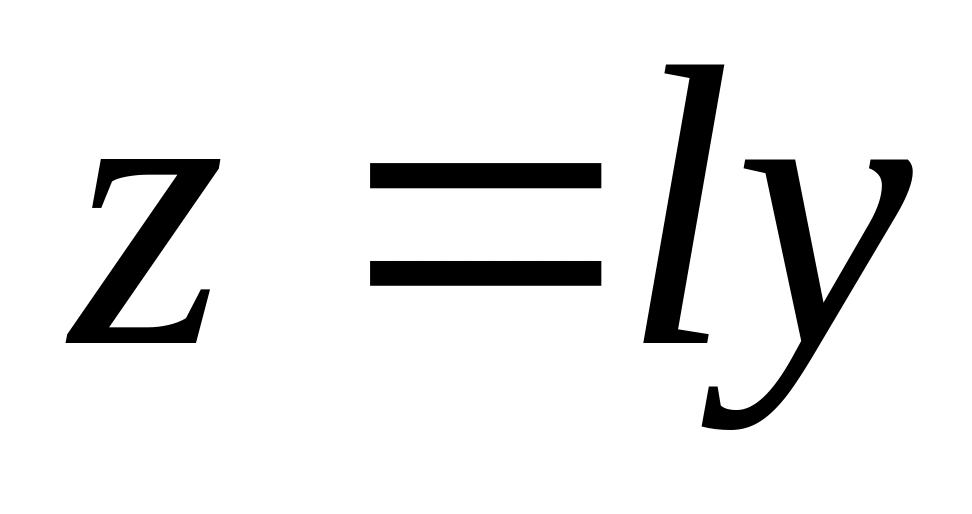 ),
то
),
то
 ,
т.е.
,
т.е.
 - транзитивность
.
Поэтому рассматриваемое отношение
является частичным порядком на множестве
А. Так как ни пара
- транзитивность
.
Поэтому рассматриваемое отношение
является частичным порядком на множестве
А. Так как ни пара
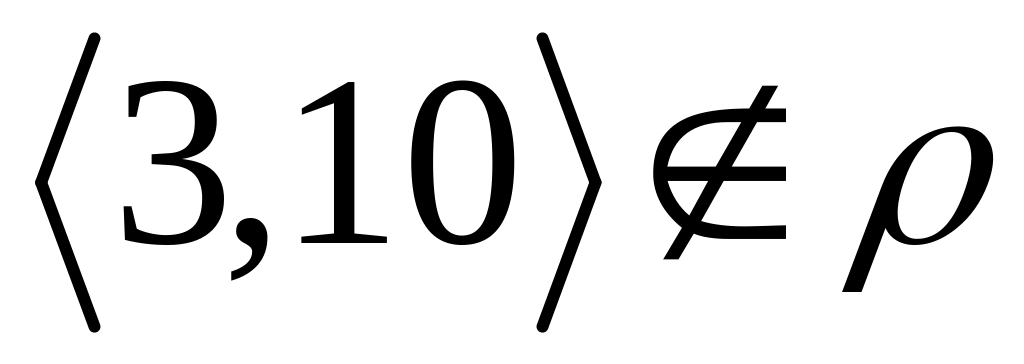 ,
ни пара
,
ни пара
 ,
то
не является на А линейным порядком.
,
то
не является на А линейным порядком.Важным примером частичного порядка на множестве М некоторых подмножеств множества А является отношение включения:
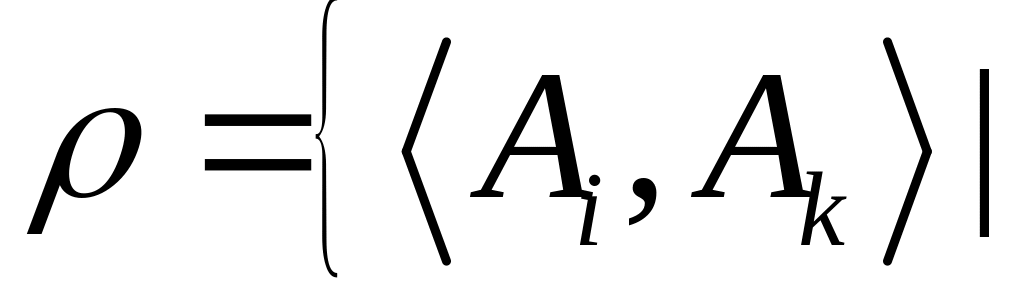
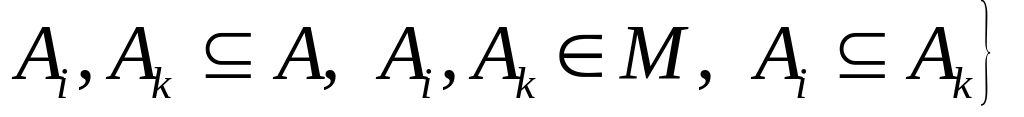 .
.Примером линейного порядка является отношение
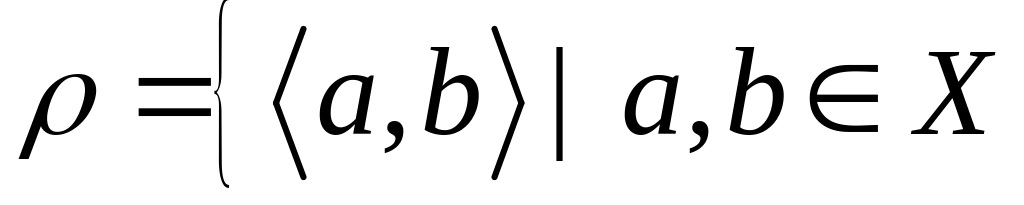 и
и
 ,
где Х – некоторое подмножество
действительных чисел
.
,
где Х – некоторое подмножество
действительных чисел
.
Контрольные вопросы и упражнения
Доказать, что для любых множеств А, В и С справедливы равенства: а)
 ;
б)
;
б)
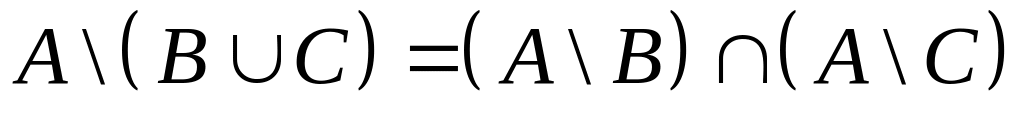 .
.Проиллюстрировать на содержательном примере некоммутативность операции разности множеств:
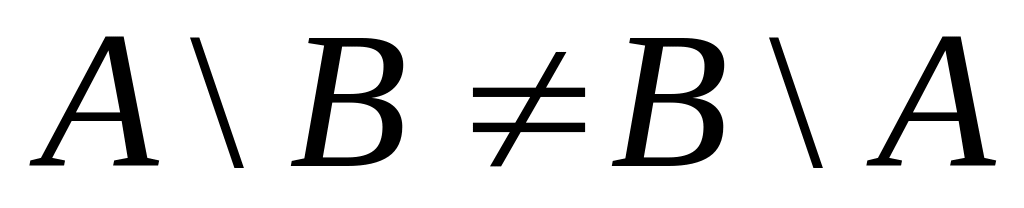 .
.Пусть

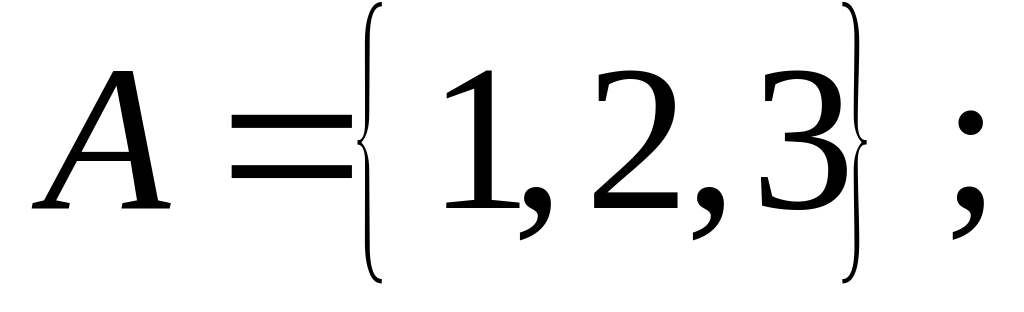

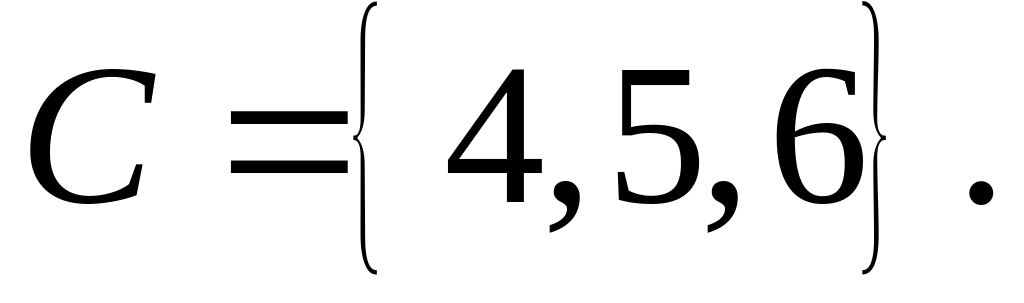 Найти множества:
Найти множества:
 ,
,
 ,
,
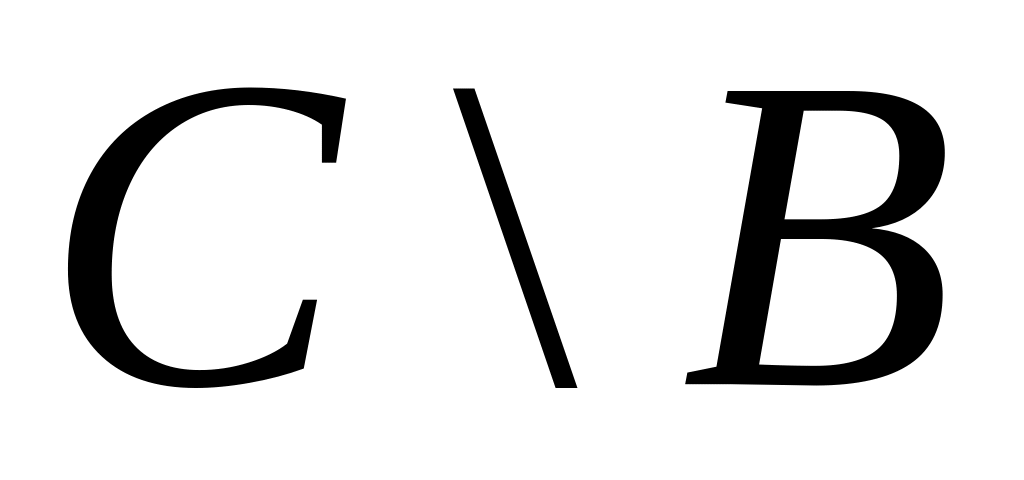 ,
,
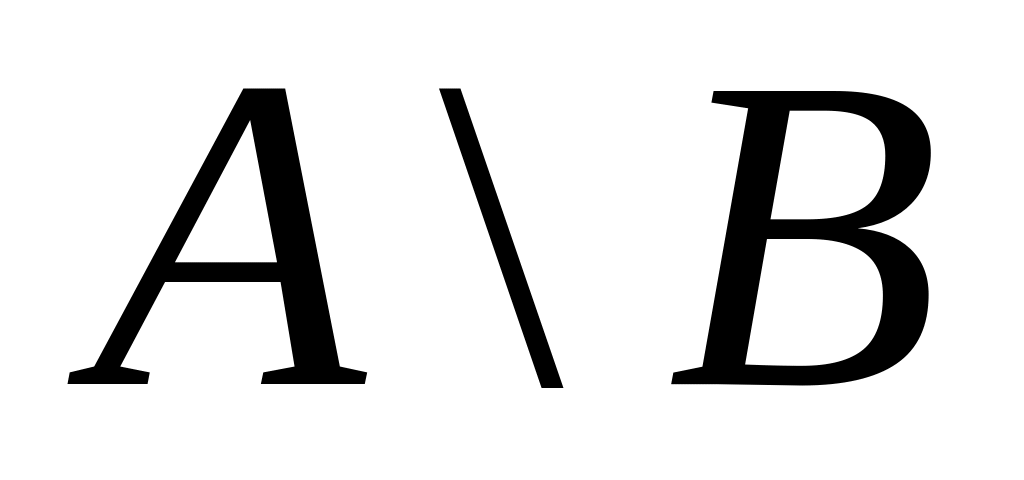 ,
,
 ,
,
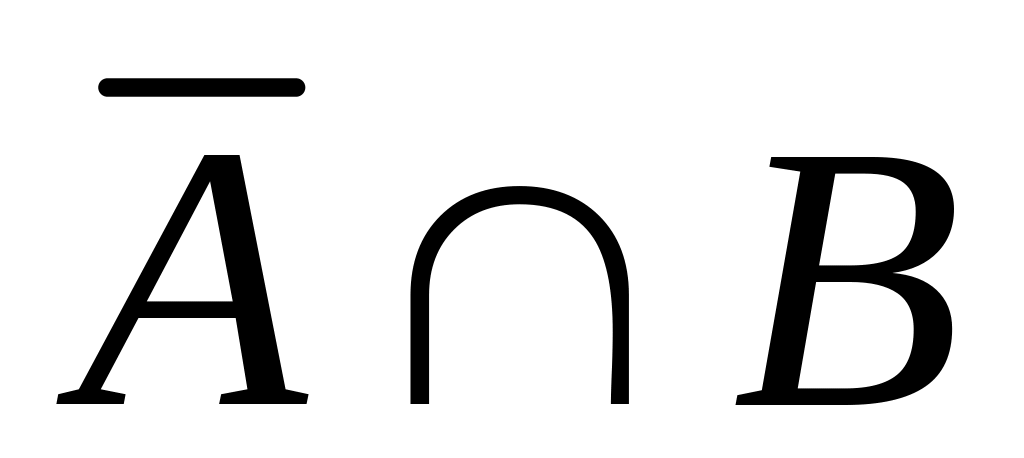 ,
,
 ,
,
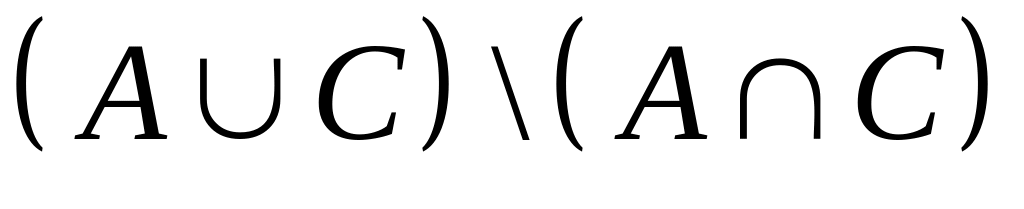 .
.Пусть универсальное множество - множество всех студентов факультета математики и информационных технологий ДонНУ,
 - множество всех студентов факультета
старше 18 лет,
- множество всех студентов факультета
старше 18 лет,
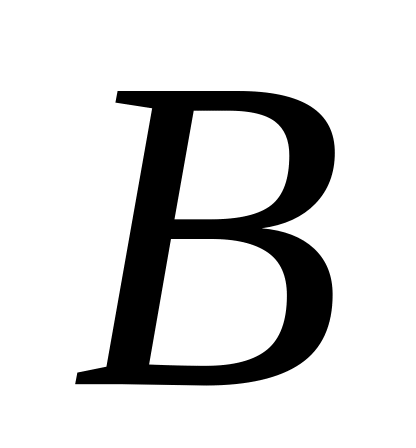 - множество всех студентов, проучившихся
на факультете более 3 лет,
- множество всех студентов, проучившихся
на факультете более 3 лет,
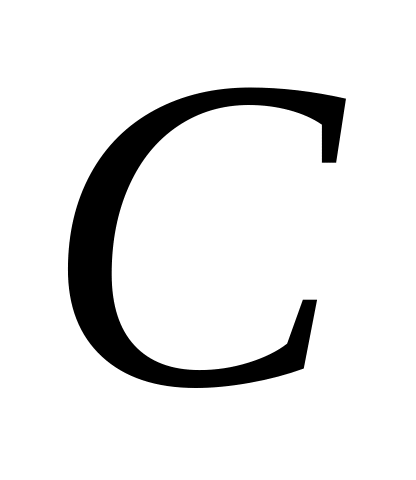 - множество отличников факультета.
Каков содержательный смысл
(характеристическое свойство) каждого
из следующих множеств:
- множество отличников факультета.
Каков содержательный смысл
(характеристическое свойство) каждого
из следующих множеств:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
д)
;
ж)
;
г)
;
д)
;
ж)
![]() ;
;
з)
;
и)
![]() ;
к)
;
к)
![]() ;
л)
;
л)
![]() ;
м)
;
м)
![]() ?
?
Выписать все двуместные отношения на множестве
 .
.На множестве построить 3 различных отношения эквивалентности и соответствующие им разбиения множества А.
Построить примеры двух отношений частичного порядка на множестве
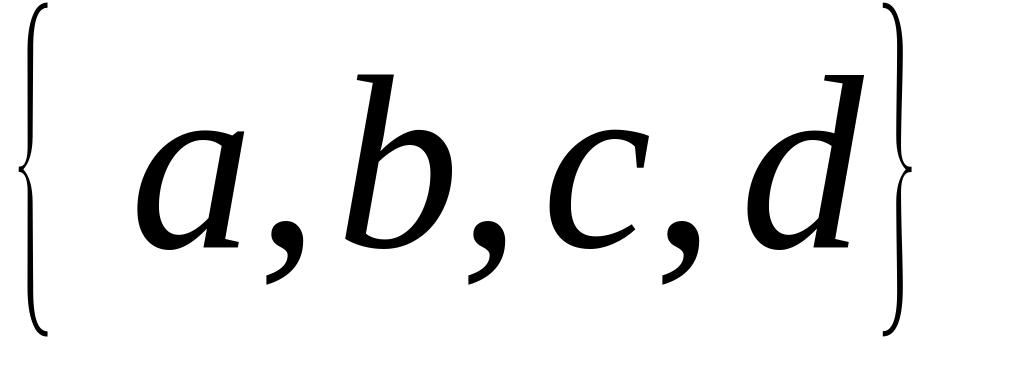 .
.Доказать:
(рефлексивность)
если
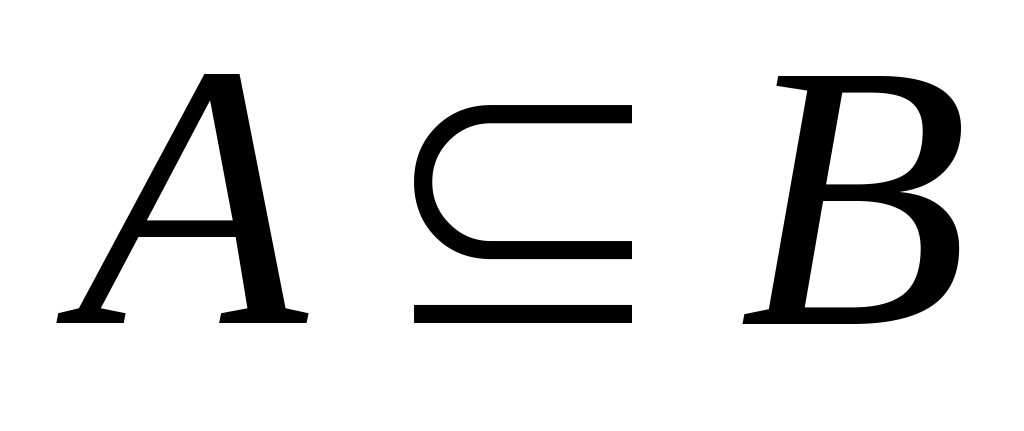 и
и
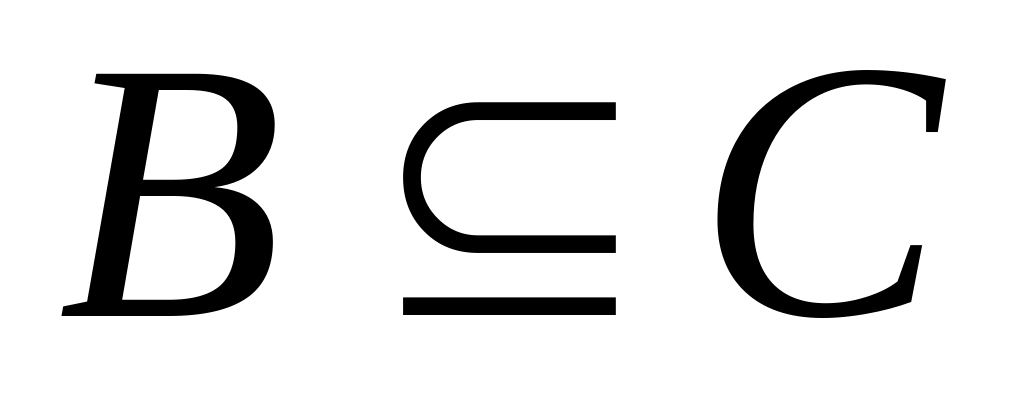 ,
то
,
то
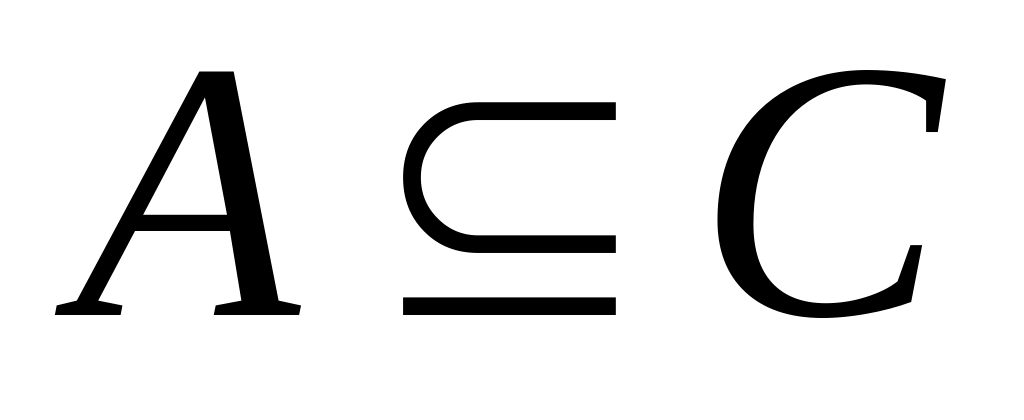 (транзитивность)
(транзитивность)