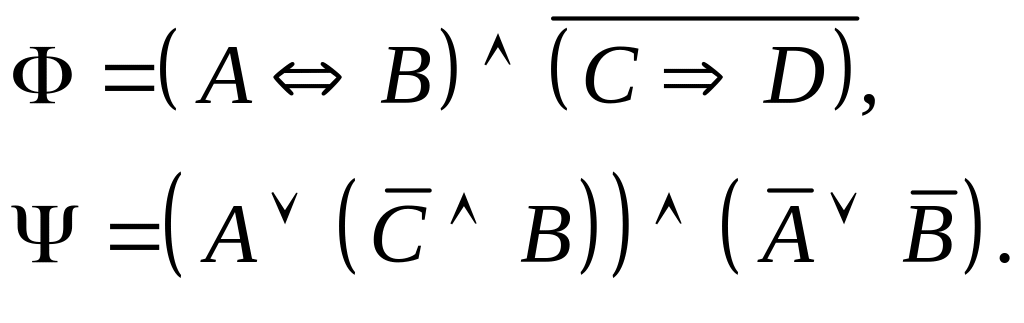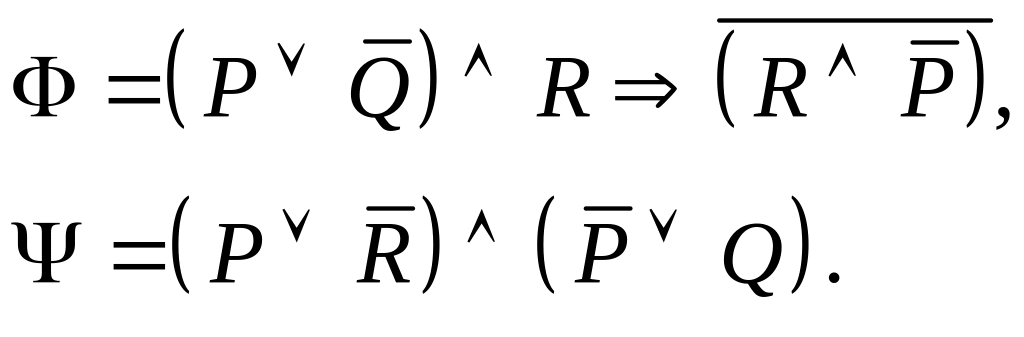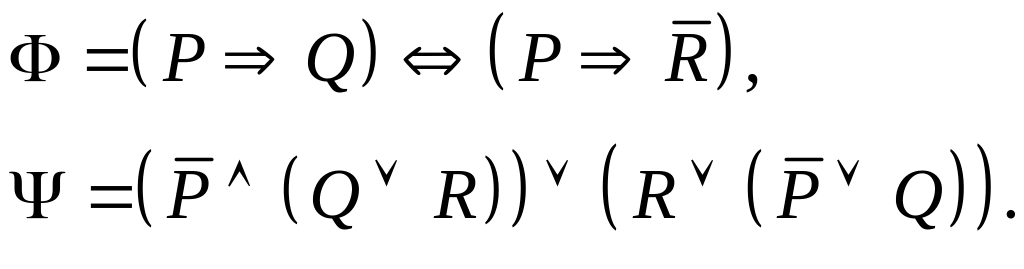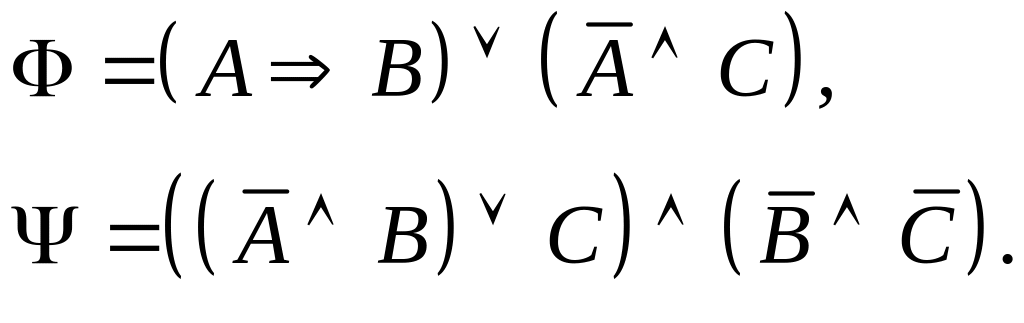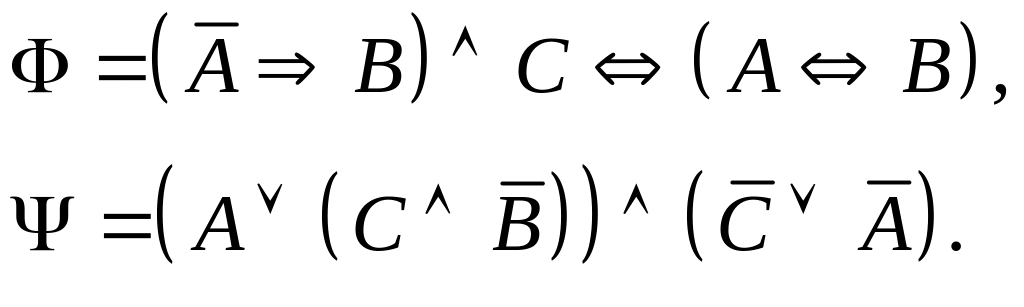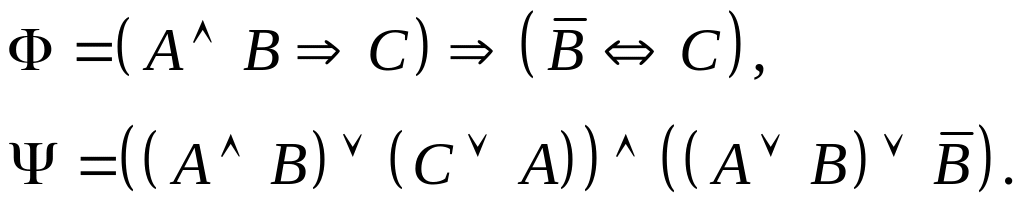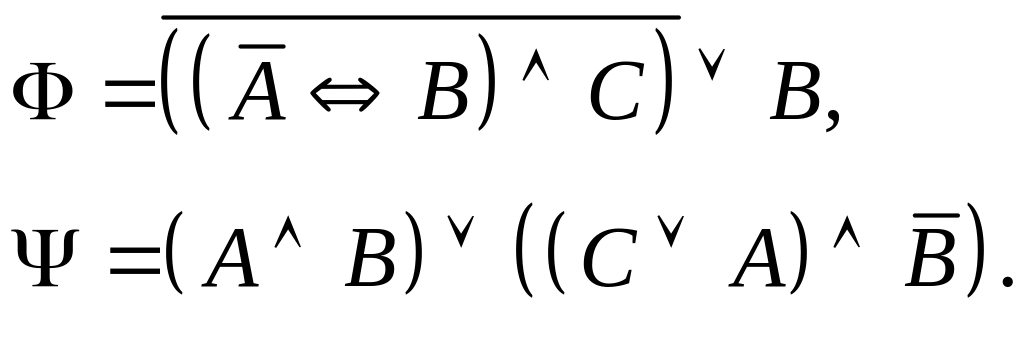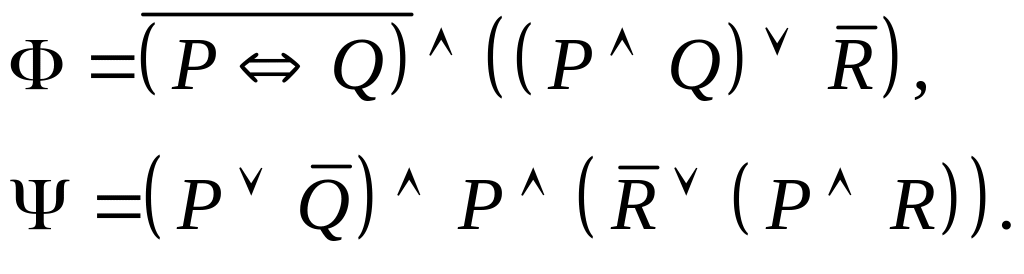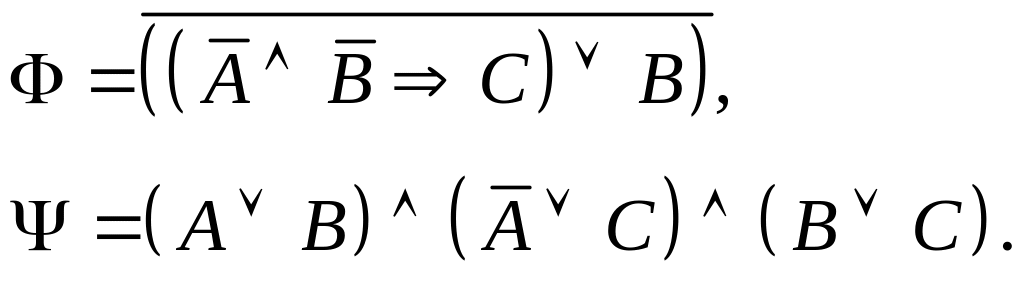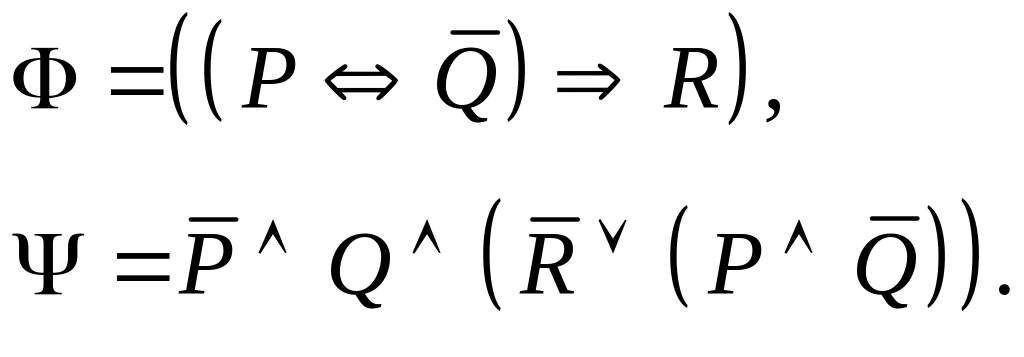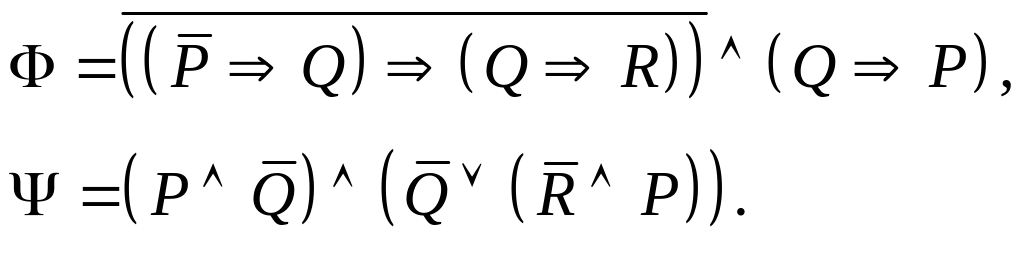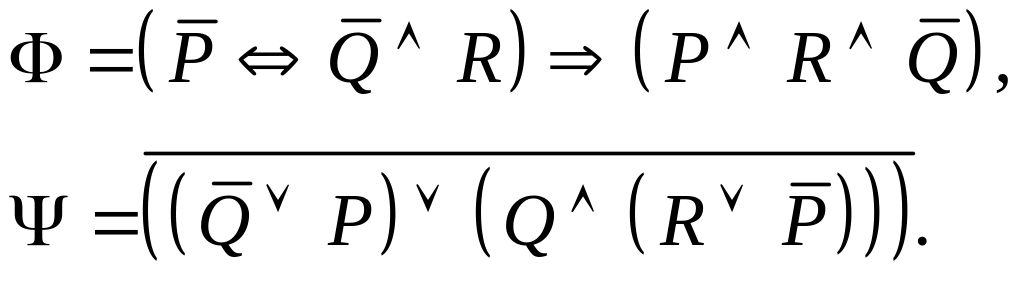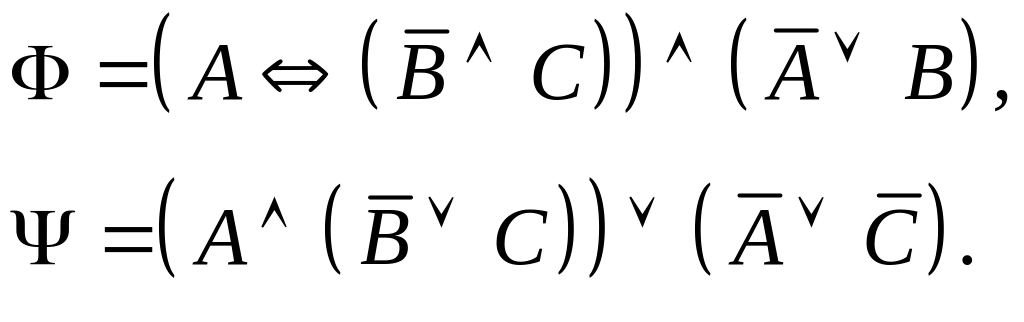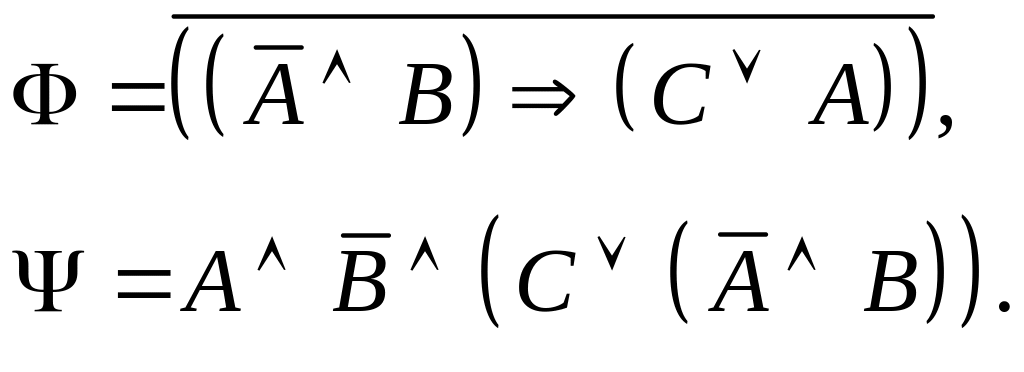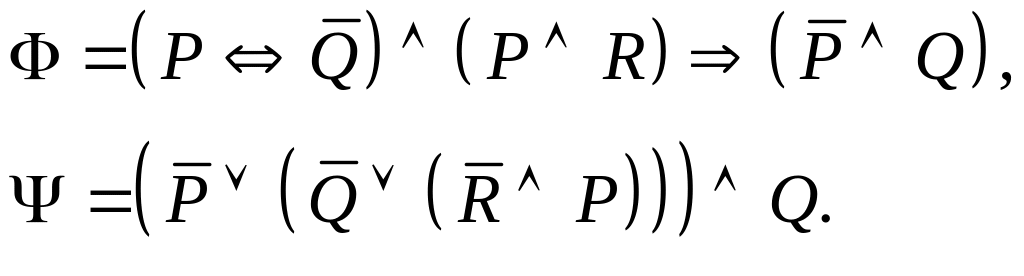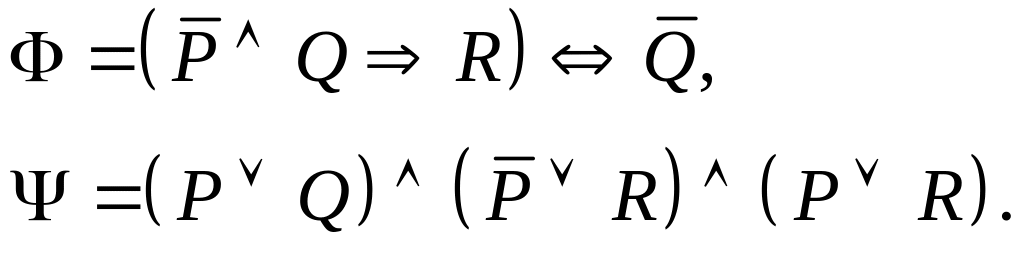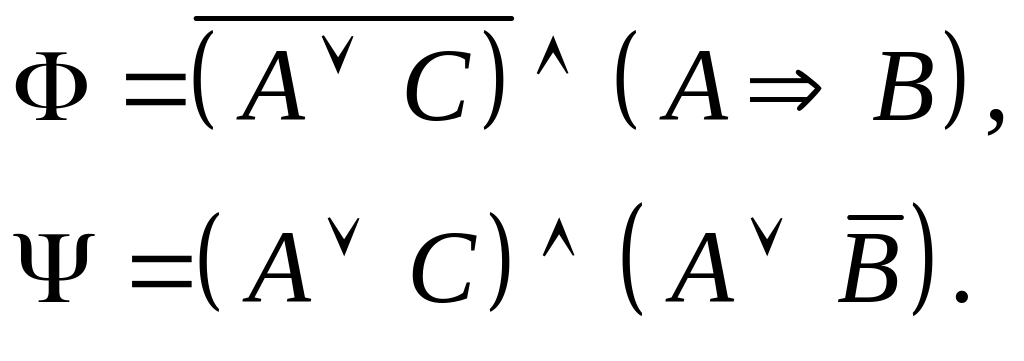Часть 2
Вторая часть содержит индивидуальные задания, предусмотренные рабочей программой курса. Приведены задачи вычислительного и теоретического характера.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ №1
МНОЖЕСТВА
Задание I. Доказать следующие тождества:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
Задание ІI. Изобразить левую и правую части тождеств из задания 1 при помощи диаграмм Эйлера-Венна.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ №2
ЛОГИКА ВЫСКАЗЫВАНИЙ
Задание I. Даны формулы и :
а) построить истинностные таблицы для формул и ;
б) привести формулы и равносильными преобразованиями к дизъюнктивной и совершенной дизъюнктивной нормальной форме;
в) для формулы построить соответствующую переключательную схему.
Задание II. Построить формулу по указанным условиям (предварительно построить таблицу истинности).
Задание III. В а проверить логичность рассуждений;
в б выяснить, совместна ли совокупность высказываний.
Задание IV. Решить указанную задачу.
I. Формулы, истинностные таблицы, нормальные формы
II. Построение формул по таблицам значений
Построить формулу от трех переменных, которая истинна тогда и только тогда, когда ровно две переменные истинны.
Построить формулу от трех переменных, которая истинна тогда и только тогда, когда истинна ровно одна из переменных.
Построить формулу от трех переменных, которая истинна тогда и только тогда, когда ровно две переменные ложны.
Построить формулу от трех переменных, которая истинна тогда и только тогда, когда ложна ровно одна из данных переменных.
Построить формулу от трех переменных, которая ложна тогда и только тогда, когда ложна ровно одна из данных переменных.
Построить формулу от трех переменных, которая ложна тогда и только тогда, когда истинны ровно две переменные.
Построить формулу от трех переменных, которая ложна тогда и только тогда, когда истинна ровно одна из переменных.
Построить формулу от трех переменных, которая ложна тогда и только тогда, когда истинны ровно две переменные.
Построить формулу от трех переменных, которая истинна тогда и только тогда, когда не менее чем две переменные принимают истинные значения.
Построить формулу от трех переменных А, В, С, которая истинна тогда и только тогда, когда В – истинна, а А – ложна.
Построить формулу от трех переменных, которая ложна тогда и только тогда, когда не менее чем две переменные принимают истинные значения.
Построить формулу от трех переменных А, В, С, которая истинна тогда и только тогда, когда А – истинна, а В – ложна.
Построить формулу от трех переменных, которая истинна тогда и только тогда, когда не менее чем две переменные принимают ложные значения.
Построить формулу от трех переменных А, В, С, которая ложна тогда и только тогда, когда А – истинна, а В – ложна.
Построить формулу от трех переменных, которая ложна тогда и только тогда, когда не менее чем две переменные принимают ложные значения.
Построить формулу от трех переменных А, В, С, которая ложна тогда и только тогда, когда В – истинна, а А – ложна.
Построить формулу от трех переменных А, В, С, которая принимает значение истина тогда и только тогда, когда А принимает значение истина.
Построить формулу от трех переменных А, В, С, которая принимает значение истина тогда и только тогда, когда все буквы принимают одинаковое значение.
Построить формулу от трех переменных А, В, С, которая истинна тогда и только тогда, когда А – ложна.
Построить формулу от трех переменных, которая ложна тогда и только тогда, когда все буквы принимают одинаковое значение.
Построить формулу от трех переменных А, В, С, которая ложна тогда и только тогда, когда А – истинна.
Построить формулу от трех переменных, которая истинна тогда и только тогда, когда не более чем одна буква принимает значение истина.
Построить формулу от трех переменных А, В, С, которая ложна тогда и только тогда, когда А – ложна.
Построить формулу от трех переменных, которая истинна тогда и только тогда, когда не более чем одна буква принимает значение ложь.