5.6. Язык алгебры предикатов.

Алгебра предикатов обладает большими возможностями в символизации обычного языка. Для записи определений или утверждений на языке алгебры предикатов не существует механических правил. В каждом конкретном случае следует передать символ утверждения с помощью символов языка предикатов.

Например, тот факт, что число А является пределом последовательности {а_n}записывают следующим образом: ε((ε>0) n₁ n((n>n₁) (|a_n-A|<ε))). Здесь n,n₁ определены на натуральных, а ε - на действительных числах.

В настоящее время зачастую применяют упрощенную запись на языке математической логики. Под квантором указывается область, откуда следует выбирать объект, на который распространяется кванторизация. Тот факт, что число А является пределом {a_n} записывают так:

(A=lim{a_n}) (ε>0) (k N) (i Ni>k)(|a_i-A|<ε)

Приведем определение непрерывности функции в точке (f(x)-непрерывна в точке a) (ε>0) (δ>0) (x R)((|x-a|< δ (|f(x)-f(a)|<ε))

Правая часть последнего соотношения на обычном языке алгебры предикатов записывается следующим образом:

ε((ε>0) δ(δ>0)  x ((|x-a|<δ) (|f(x)-f(a)|<ε))

Запись утверждений на языке математической логики позволяет преобразовывать их к равносильной, но более удобной с какой-либо точки зрения форме, используя аппарат алгебры предикатов.

Пример. Тот факт, что последовательность {a_n} имеет конечный предел, записывают в виде

A ε((ε>0) n₁ n(n>n₁) (a_n-A)<ε))),

что равносильно A ε( (ε>0) n₁ n( (n>n₁) (|a_n-A<ε|)))

Отсюда, следуя правилам алгебры предикатов, легко получить отрицание этого высказывания A ε((ε>0) n₁ n((n>n₁)(|a_n-A|)<ε)). Как и выше, n,n₁ определены на натуральных , а ε,A - на действительных числах.

5.7. Понятие об исчислении предикатов.

Об исчислении предикатов студенты знакомятся в обзорном порядке. При построении аксиоматической теории предикатов вводится список предикатных переменных, предикатных символов и простых формул, аналогичный рассмотренному ранее. Формулами исчислений предикатов являются:

1. простые формулы;

2. если Φ и Ψ – формулы, то Φ, (Φ Ψ), x Φ – формулы;

3. других формул нет.

Набор схем аксиом исчисления предикатов включает в себя три схемы аксиом исчисления высказываний, кроме того, еще две схемы аксиом:

u(Φ(u) Φ(t)), где Φ(u) – формула, t - переменная, свободная для u в Φ(u) т.е., никакое свободное вхождение t в Φ не лежит в области действия квантора u;

б) u (Φ ψ) (Φ u Ψ) где Φ не содержит свободно u (правило обобщения).

Правил вывода два:

1. Из Φ Ψ и Φ следует Ψ

2. Из Φ следует u Φ

Как и в исчислении высказываний вводится понятие вывода, выводимости из гипотез Г и т.п.

При изучении исчисления предикатов следует обращать внимание на новые моменты, возникающие в сравнении с исчислением высказываний.

Например, теорема о дедукции читается так.

Пусть Г,Φ├Ψ и пусть существует такой вывод Ψ из Г и Φ, в котором ни при каком применении правила обобщения к формулам, зависящим от Φ, не связывается квантором никакая свободная переменная формулы Φ. Тогда

Г├Φ Ψ

Как и в исчислении высказываний справедлива теорема о том, что выводимыми в исчислении предикатов являются тавтологии, и только они.

Контрольные вопросы и упражнения

1. Как истолковать с точки зрения алгебры предикатов системы уравнений, неравенств? Совокупности неравенств?

2. Выяснить геометрический смысл высказывани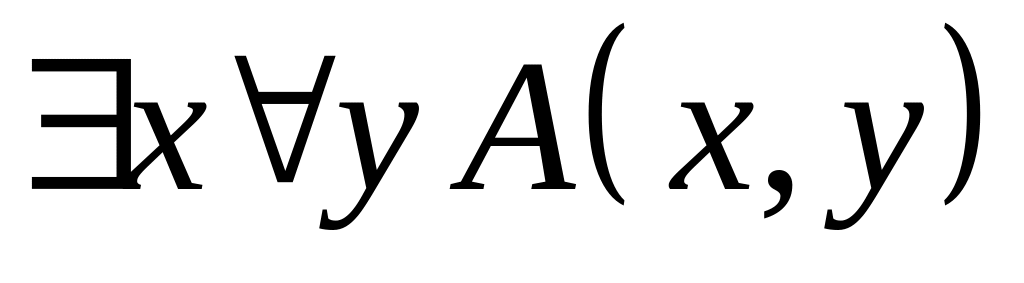й и 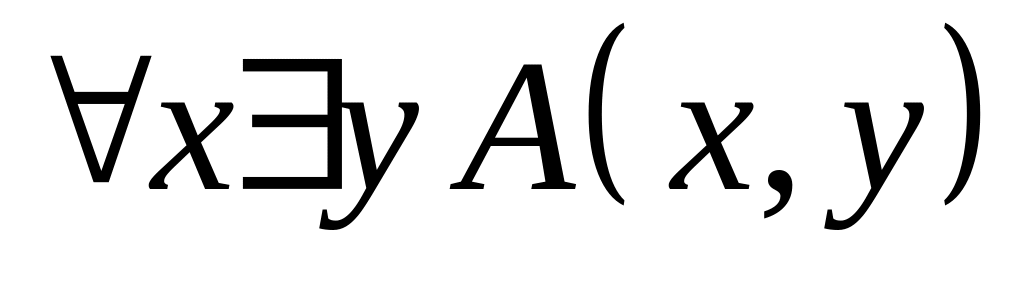, где х, у определены на вещественных числах.

3. Свободна ли переменна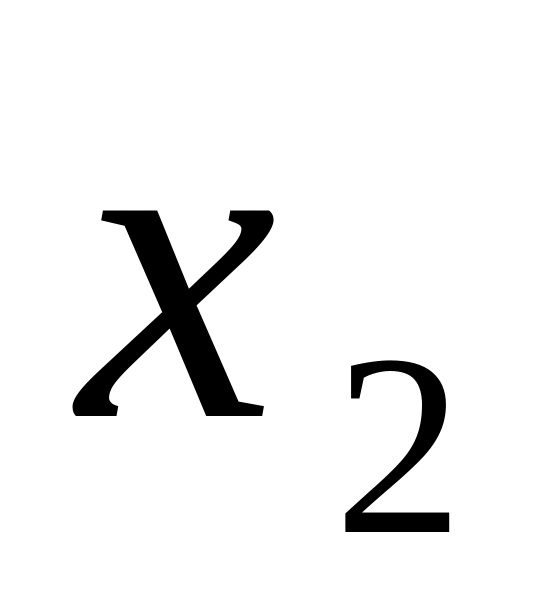я для 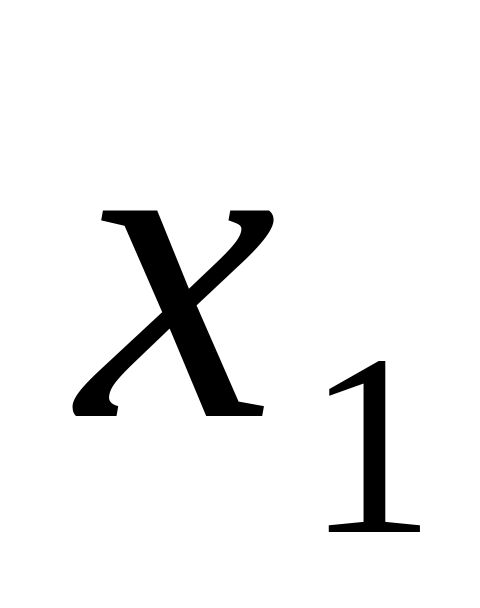в формулах:

а) ;

б) .

4. Записать с помощью логико-математической символики полное решение следующих уравнений и неравенств:

а) ; в) ;

б) ; г) .

5. Записать с помощью логико-математической символики:

а) определение предела в точке;

б) утверждение, что каждое квадратное уравнение с действительными коэффициентами, у которого дискриминант строго положителен, имеет точно два вещественных корня;

в) утверждение, что две различные прямые пересекаются не более чем в одной точке;

г) определение последовательности функций , сходящейся на интервале .

6. Записать с помощью логико-математической символики следующие утверждения и построить их отрицания, используя законы алгебры предикатов:

а) определение непрерывности функции в точке ;

б) определение непрерывности функции на ;

в) аксиому параллельности евклидовой планиметрии;

г) определение последовательности функций , равномерно сходящейся на .

7. Записать с помощью логико-математической символики достаточное и необходимое условия существования действительного корня для уравнения 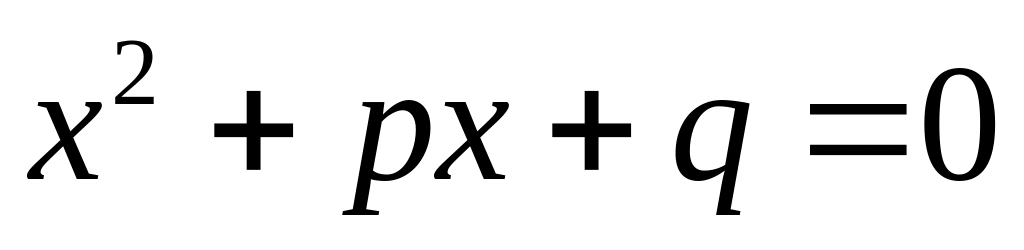. Равносильны ли они соответственно таким условиям:

а) ;

б) .

8. Построить выводы:

а) ;

б) .