Часть 1
В первой части методического пособия раскрыта содержательная основа программного материала по курсу математической логики. Основные понятия курса и теоремы иллюстрируются примерами, приведены образцы решения типовых задач, предложены контрольные вопросы и упражнения для самостоятельного решения.
Тема I множества и операции над ними. Отношения
Множества. Равенство множеств
Множеством называется совокупность
М некоторых объектов (элементов),
мыслимая как единое целое. Если а –
элемент множества, то пишем
,
если
не является элементом М, то пишем
.
Пусть каждый элемент множества В
является элементом множества А,
тогда множество В называется
подмножеством множества А
(обозначается
).
Ясно, что для любого множества А
всегда имеет место
.
- означает пустое множество,
т.е. множество, не имеющее ни одного
элемента. Полагают, что
для любого множества А.
Аксиома экзистенциальности
(аксиома объемности) утверждает, что
каждое множество однозначно определяется
своими элементами. Если
- все элементы множества А, то можно
записать
.
При этом не предполагается, что все
элементы
попарно различны. Одно и то же множество
можно обозначать многими способами,
например,
.
В дальнейшем целесообразно считать, что если , то все попарно различны.
Если
,
то для множеств
и
верно, что
и
,
но множество
не является подмножеством А
(обозначается
),
так как элемент
.
Если
,
то множество А имеет 8 различных
подмножеств:
.
Обращаем внимание, что следует различать
элемент а и множество
,
единственным элементом которого является
а.
,
так как
- одноэлементное, но не пустое множество,
единственным элементом которого является
пустое множество
.
Множество М можно задавать указанием
какого-либо свойства Р, которым
обладают все элементы множества М
и не обладает ни один элемент, не
принадлежащий М, что обозначается
через
.
Например,
,
для некоторого
- множество всех четных натуральных
чисел.
Алфавит – это множество, элементами
которого являются элементарные
(неразложимые) знаки, называемые также
буквами. Например, множество А,
состоящее из десяти арабских букв, можно
принять за алфавит. Другой пример
алфавита – это множество, состоящее из
заглавных букв латинского алфавита.
Алфавит
содержит бесконечное множество букв,
считаем, что
отлично от
,
если
,
рассматривается как единый символ.
В дальнейшем будем считать, что все
рассматриваемые множества являются
подмножествами некоторого фиксированного
множества
,
которое называется универсальным.
Алгебра множеств
Объединением множеств А и
В (обозначается через
)
называется множество, элементы которого
принадлежат хотя бы одному их множеств
А или В.
.
Пересечением множеств А и
В (обозначается через
)
называется множество, элементы которого
принадлежат одновременно множеству А
и множеству В.
Множества А и В называется
непересекающимися, если
.
Разностью множеств А и В
(обозначается через
)
называется множество, элементы которого
принадлежат А и не принадлежат В.
Разность
называется дополнением множества
А и обозначается через
.
Симметрической разностью
множеств А и В (обозначается
через
)
называется объединение разностей
и
.
Для графической иллюстрации отношений, которые могут иметь место между подмножествами универсального множества , часто используют так называемые диаграммы Эйлера-Венна: универсальное множество изображается множеством точек некоторого прямоугольника, а его подмножества – в виде кругов. Так, множества , , изображаются областями, заштрихованными на соответствующих рисунках
Свойства операций над множествами. В рекомендуемой литературе указан ряд свойств операций над множествами. Заметим при этом, что в учебных пособиях рассматривают и другие операции над множествами (например, симметрическую разность), но при первоначальном ознакомлении с алгеброй множеств целесообразно ограничиться изучением четырех важнейших операций, а также их основных свойств, которые сформулированы в виде теоремы.
Теорема. Для любых множеств А и В справедливы следующие равенства:
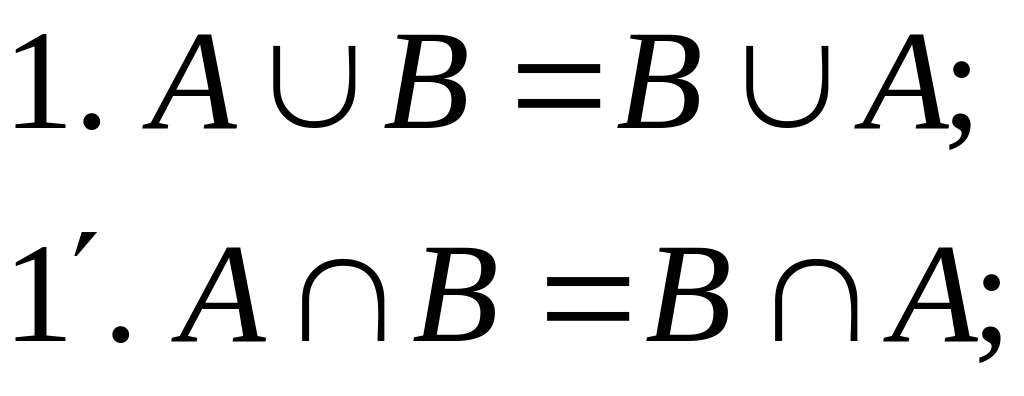(коммутативность)
(ассоциативность)
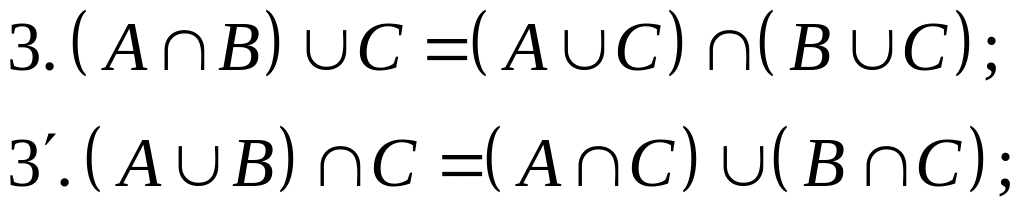(дистрибутивность)
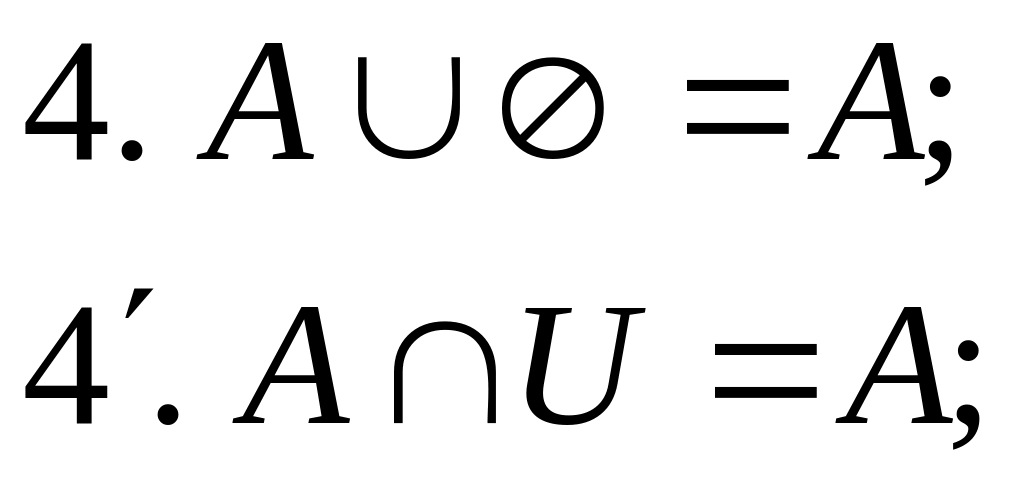
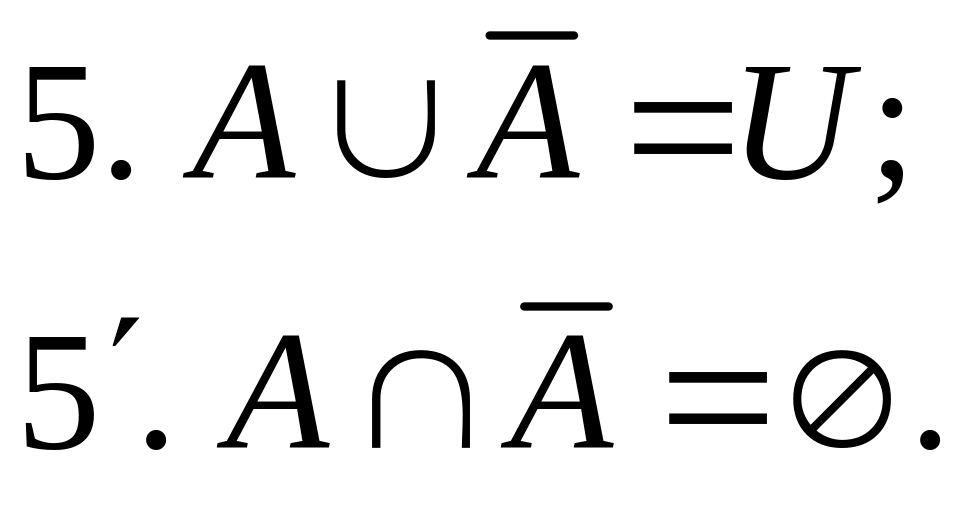
В качестве примера приведем доказательство
равенства 3 (остальные равенства
доказываются аналогично). Пусть х
– произвольный элемент
:
но
тогда и только тогда, когда х
принадлежит хотя бы одному из этих
множеств, т.е. 1)
или 2)
.
А
тогда и только тогда, когда
и
одновременно. Но 1)
и
или 2)
тогда и только тогда, когда
и
.
Но
и
тогда и только тогда, когда
.
Итак, мы доказали, что
тогда и только тогда, когда
,
т.е. множества
и
состоят из одних и тех же элементов, и,
следовательно, равенство 3 верно. Подобное
доказательство этой теоремы, также как
и другие свойства операций над множествами,
можно найти в [1] с. 29-33.