4. Электрические цепи однофазного синусоидального тока

Синусоидальный ток (ЭДС, напряжение) представляет собой ток, изменяю-щийся во времени по синусоидальному закону

(17)

где I_m – амплитуда тока, T – период, f=1/T - частота, (ωt+Ψ₀) – фаза, Ψ₀ – начальная фаза.

Синусоидальный ток ( ЭДС и напряжение) принято изображать на комплексной плоскости в виде вектора для момента времени t=0

, (18)

где - комплексная величина, ее модуль равен I_m , а угол, под которым вектор проведен к оси +1 на комплексной плоскости, равен начальной фазе Ψ₀. В расчетах, обычно, применяют действующие значения синусоидальных величин. Под комплексом действующего значения тока ( ЭДС, напряжения) или под комплексом тока, понимают величину, определяемую по формуле

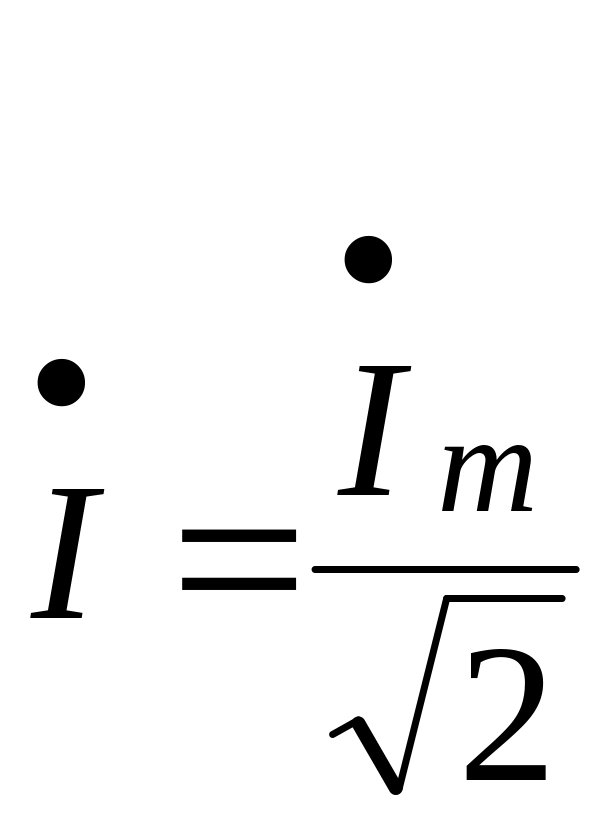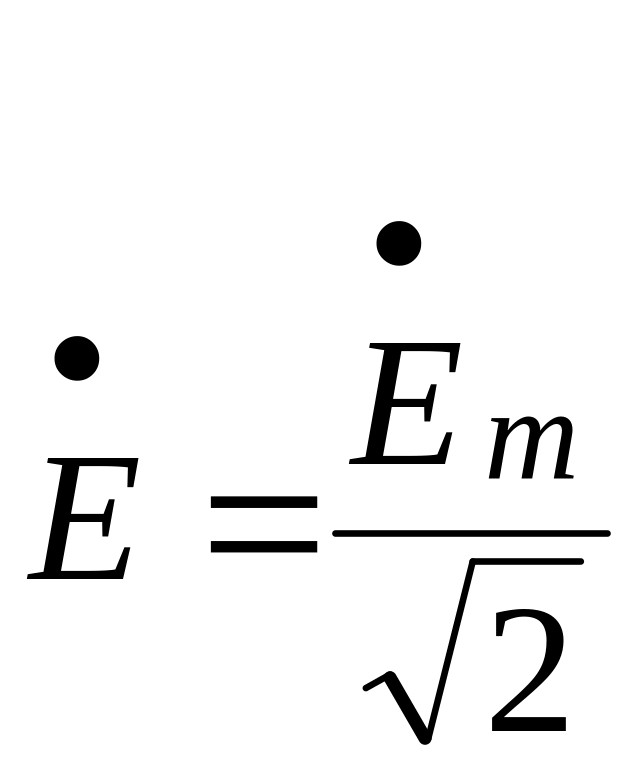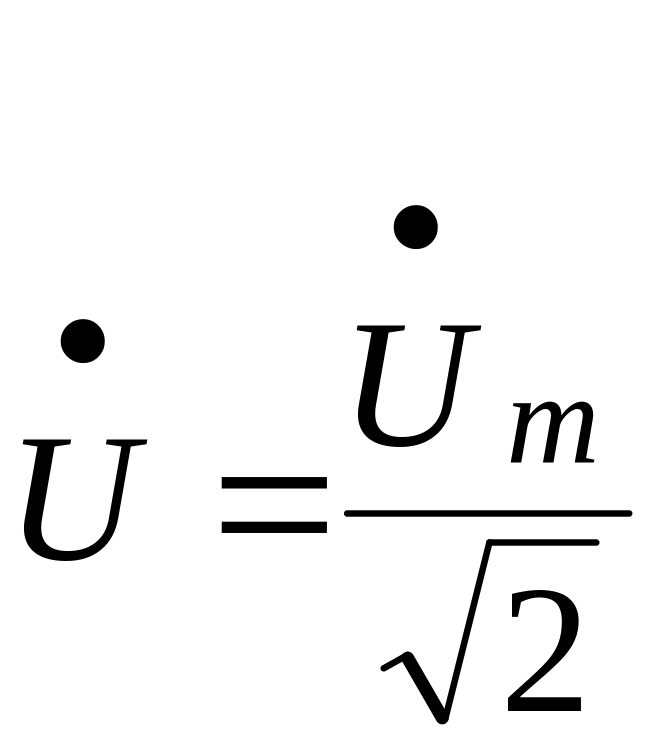( , ) . (19)

В цепях переменного тока кроме активного сопротивления R, имеют место реактивные сопротивления X: индуктивное - X_L и емкостное - X_C . Комплексное поллное сопротивление в алгебраической форме имеет вид

Z = R + јХ_L- јХ_C , (20)

где Х_L =ωL = 2πfL; L - индуктивность; Х_C=1/ ωC=1/ 2πfC; С- емкость конденсатора.

Как и всякий комплекс, Z можно записать в показательной форме. Модуль комплексного сопротивления принято обозначать z. Точку над Z не ставят, так как ее принято ставить над комплексными величинами, которые являются синусоидальными функциями времени. Модуль комплексного сопротивления z можно представить как гипотенузу прямоугольного треугольника сопротив-лений, один катет которого равен R, другой Х (рис. 7), тогда

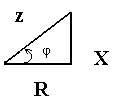
(21)

Рис.7

Комплексное сопротивление в показательной форме будет имееть вид:

. (22)

Закон Ома и законы Кирхгофа для цепи синусоидального тока в комплексной форме будут иметь вид

; ; . (23)

Применение векторных диаграмм при расчете электрических цепей синусоидального тока.

Если в электрической цепи, кроме активного сопротивления, имеют место реактивные сопротивления, то токи и напряжения на различных участках цепи (исключая участок с активным сопротивлением) не совпадают по фазе. Наглядное представление о фазовом расположении различных векторов дает векторная диограмма токов и напряжений. Качественный контроль заключается в сравнении направлений различных векторов на комплексной плоскости, которые получают при аналитическом расчете, с направлением этих векторов исходя из физических соображений. Кроме того, векторная диограмма используется как средство расчета в методе пропорциональных величин.

Баланс мощностей в цепи переменного тока.

В цепях переменного тока различают активную Р, реактивную Q и полную S мощности. Среднее значение мгновенной мощности за период называется активной мощностью, она затрачивается на создание полезной работы. Активная мощность определяется по формуле

. (24)

Активную мощность измеряют в ваттах (Вт).

Под реактивной мощностью Q понимают мощность, определяемую по формуле

. (25)

Реактивную мощность измеряют в вольтамперах реактивных (вар), она может быть как положительной, так и отрицательной. Реактивная мощность пропорциональна среднему за четверть периода значению энергии, которая отдается источником питания на создание переменной составляющей электрического и магнитного поля индуктивности и емкости.

Полная S (кажущаяся) мощность равна произведению действующих напряжения и тока

. (26)

Единица измерения полной мощности вольтампер (В∙А).

Между Р, Q и S существует сявзь

Р²+ Q²=S². (27)

Запись полной мощности в комплексной форме имеет вид

, (28)

где значок ~ (тильда) над S означает комплекс полной мощности, - комплекс напряжения, - сопряженный комплекс тока ( комплекс тока, у которого знак перед мнимой частью меняется на противоположный, например , а ).

В цепях переменного тока, как и в цепях постоянного тока, соблюдается баланс мощностей: сумма мощностей источников равна сумме мощностей приемников:

(29)

или в комплексной форме

(30)

Пример 2.

Для схемы, изображенной на рис.8 выполнить следующее:

1. Записать в алгебраической, показательной, тригонометрической формах

комплексные выражения ЭДС и полных сопротивлений.

2. Записать уравнения методом контурных токов.

3. Определить действующие значения напряжений на участках цепи и токи в

ветвях электрической цепи методом эквивалентирования.

4. Построить векторную диаграмму токов и напряжений.

5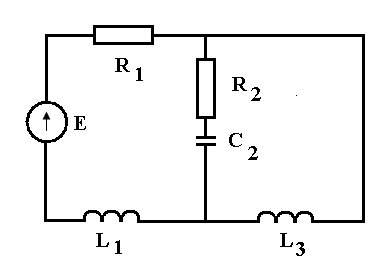 . Составить баланс мощностей.

Рис. 8

Параметры элементов схемы:

E = 120B; f = 60 Гц; С₂ = 379 мкФ; L₁ = 26,5 мГн; L₃ = 21,2 мГн; R₁ = 2 Ом;

R₂ = 5 Ом.

Решение

1. Запишем в алгебраической, показательной, тригонометрической формах комплексные выражения для ЭДС и полных сопротивлений.

Значение ЭДС задано действительным числом, равным 120 В.

На комплексной плоскости ЭДС будет совпадать с осью вещественных чисел (рис. 9), следовательно угол φ = 0.

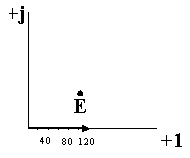
Рис. 9

Запись комплексной ЭДС в показательной степени будет иметь вид:

= Ee^j0 (В), в тригонометрической форме = Е٠cosφ = E٠cosφ0⁰ = 120 (B).

Алгебраическая запись ЭДС будет иметь вид: = Е٠1 + јE٠0⁰ = E = 120 (В).

В рассматриваемой схеме имеются три ветви, каждой из которых соответствует полное комплексное сопротивление: Z₁, Z₂, Z₃, соответственно.

Изобразим на комплексной плоскости полные сопротивления. В направлении, совпадающем с направлением вещественной оси, откладываем активные сопротивления: R₁ = 2 Ом; R₂ = 5 Ом; R₃ = 0 Ом. В направлении, совпадающем с осью мнимых чисел, откладываем реактивные сопротивления:

X_L по оси +ј, Х_с – по оси –ј.

Значения индуктивных и емкостного сопротивлений определяем по формулам:

X_L = ωL = 2 π٠f٠L ;

X_c = 1/ ωC =1/2 π٠f٠C ;

X_L1 = 2 ٠ 3,14 ٠60 ٠26,5 ≈ 10 (Ом);

X_L3 = 2 ٠ 3,14 ٠60 ٠21,2 ≈ 8 (Ом);

Х_с =

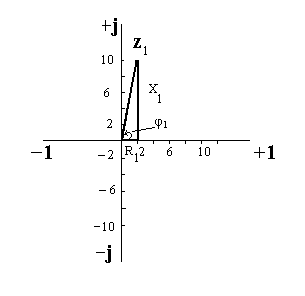На рис. 10 ,11,12 показаны полные комплексные сопротивления Z₁, Z₂, Z₃.

Рис. 10

Алгебраическая запись комплексного сопротивления имеет вид: Z = R ± јХ, модуль сопротивления определяется по формуле:

z = | Z | =

Полные комплексные сопротивления в алгебраической форме будут иметь вид:

Z₁ = 2 + ј10 (Ом);

Z₂ = 5 – ј7 (Ом);

Z₃ = 0 + ј8 (Ом).

Модули полных сопротивлений составят:

z₁ = = 10,198 (Ом);

z₂ = = 8,6023 (Ом);

z₃ = 8 (Ом).

Для записи выражений комплексных сопротивлений в тригонометрической и показательной формах определим углы между активными и полными сопротивлениями из треугольников сопротивлений:

tgφ₁ = ; φ₁ ≈ 79⁰ ; tgφ₂ = ; φ₂ ≈ -55⁰; φ₃ =90⁰.

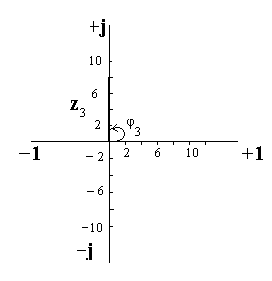
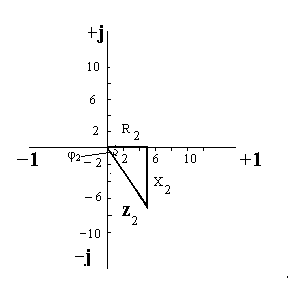
Рис.11 Рис.12

Тригонометрическая запись полных комплексных сопротивлений:

Z₁ = z₁cosφ₁ + јz₁sinφ₁=10,198٠cos79⁰+ј10,198sin79⁰;

Z₂ = z₂cosφ₂ + јz₂sinφ₂ =8,6023٠cos55⁰-ј8,6023sin55⁰;

Z₃ = 8٠cos90⁰ + ј8sin90⁰.

Запишем полные комплексные сопротивления в показательной форме:

Z₁ = 10,198 е^ј79°; Z₂ = 8,6023 е ^-ј55°; Z₃ = 8 ٠е^ј90°.

2. В рассматриваемой схеме два независимых контура. Обозначение их как I и П. Контурные токи в этих контурах обозначим как I₁₁ и I₂₂ (рис.13)

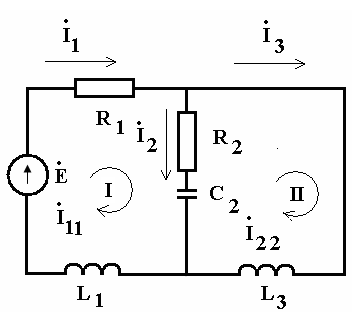
Рис. 13

Запишем для рассматриваемой схемы уравнения методом контурных токов:

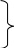
3. Метод эквивалентирования заключается в последовательном преобразовании исходной схемы, представленной на рис.14 в схему на рис.15, а затем в схему (рис.16):

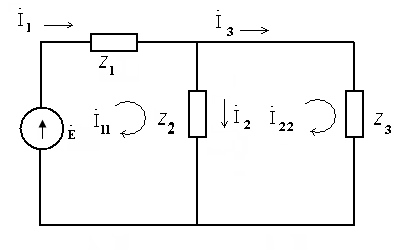
Рис.14

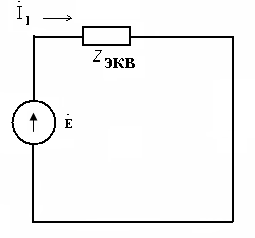
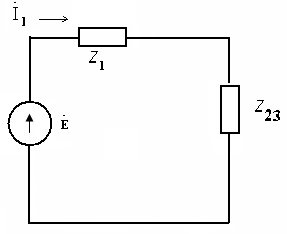
Рис. 15 Рис. 16

Полные сопротивления Z₂ и Z₃ включены параллельно, заменим их эквивалентным сопротивлением Z₂₃

Z₂₃ =

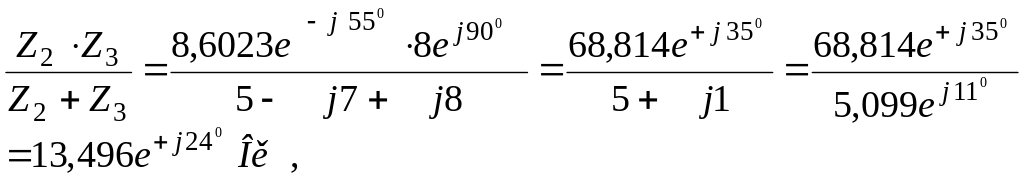
или в алгебраической форме

Z₂₃ =13,496٠cos24⁰ + j13,496 ٠sin24⁰ = 12,31+ j5,54 (Ом).

Сопротивления Z₁ и Z₂₃ включены последовательно, поэтому

Z_экв = Z₁ + Z₂₃ =12,31+ j5,54 +2+ j10 = 14,31 + j15,54 (Ом).

В показательной форме:

Z_экв = 21,13 (Ом).

Ток İ₁ определим по формуле

İ₁=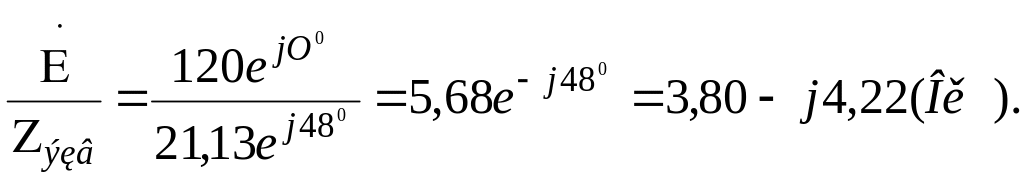

Напряжение Ù₁₂ на сопротивление Z₂₃ составит

Ù₁₂ = İ₁Z₂₃ = 5,68 ٠ ٠ 13,5 = 76,68 ٠ = 70,06 – j31,17 (В).

Напряжение Ù₁₂ можно также определить

Ù₁₂ =È-İ₁Z₁ = 120-5,68 ٠ ٠10,198 е^ј79° =120-57,94 =70,33-j29,83 (В).

Ветви с сопротивлениями Z₂ и Z₃ включены параллельно, поэтому токи I₂ и I₃ определяем по формулам:

İ₂ = 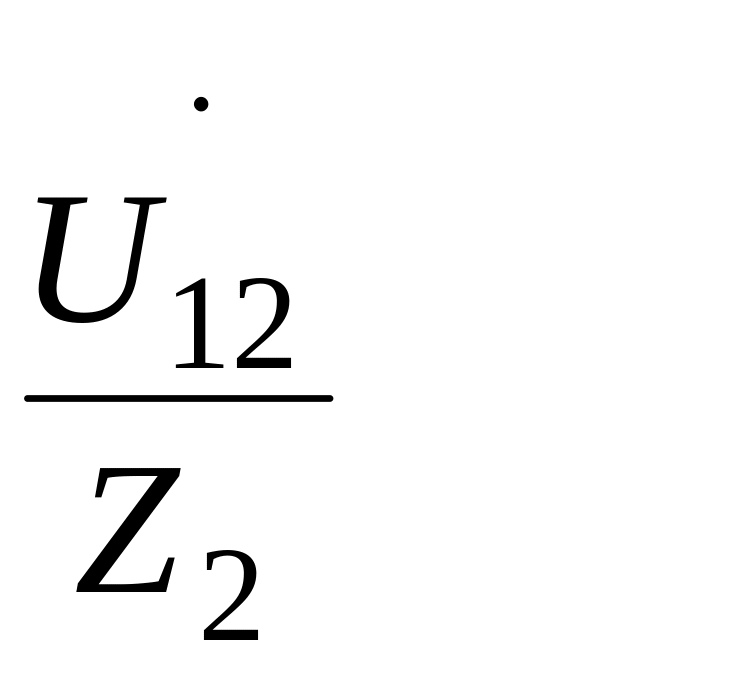İ₃ =

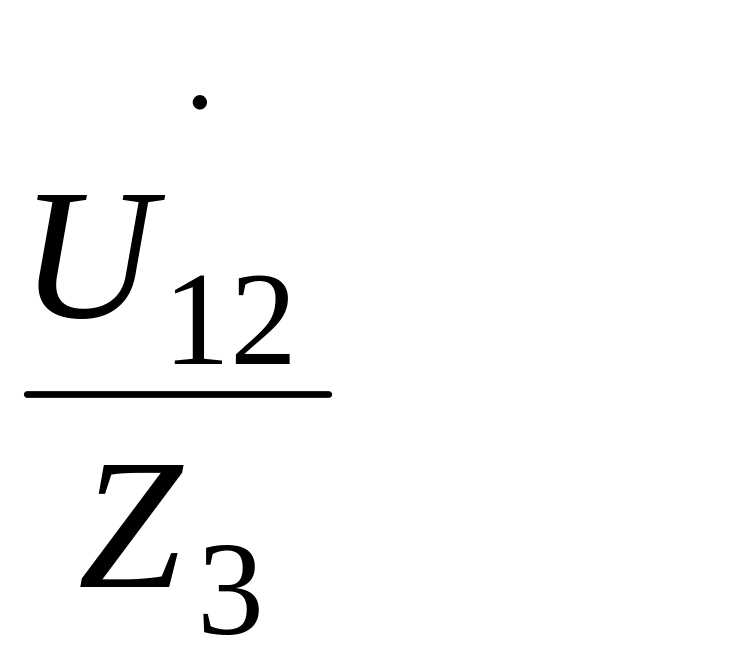
İ₂ =

İ₃ =

Правильность выполненных расчетов проверим, используя первый закон Кирхгофа

İ₁ = İ₂ + İ₃

3,80 – j4,22 = 7,65 + j4,59 – 3,89 – j8,76 ;

3,80 – j4,22 = 3,80 – j4,22 (А).

4. Составим баланс мощностей для рассматриваемой схемы.

Полная мощность источника питания составит:

= 120(3,80 + j4,22) = 456,00 + j506,40 (В٠А).

Суммарная мощность приемников электроэнергии равна:

,

где 5,68²(2 +j10) = 64,53 + j322,63 (В٠А);

8,92²(5 – j7) = 397,83 – j556,97 (В٠А);

9,59² ٠ j8 = j735,75 (вар);

462,36 + j501,40 (В٠А).

Модули мощности источника и приемника равны

682,04 (В٠А); 681,45 (В٠А).

Погрешность расчетов составляет:

∆% = .

5. Построим векторную диаграмму токов и напряжений на основе полученных расчетных значений (рис.17) и рассчитав напряжение на сопротивлении Z₁

Ù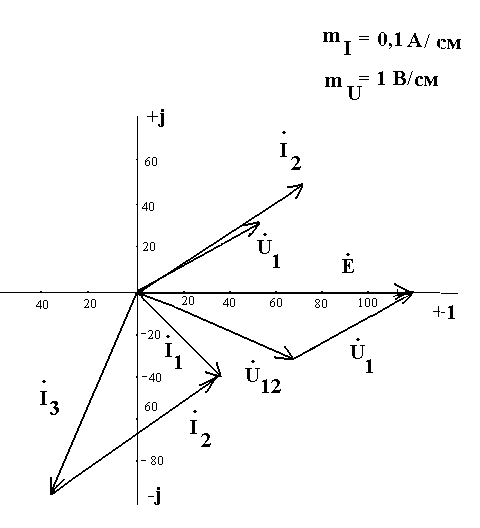 ₁ = İ₁Z₁ = 5,68 ٠ ٠ 10,198 = 57,925 ٠ (В)

Рис.17