Основная теорема теории игр. Всякая конечная антагонистическая игра 2-х лиц имеет цену и у каждого игрока имеется, по меньшей мере, одна оптимальная стратегия.
Как и большинство фундаментальных математических теорем о существовании решения, данная теорема не позволяет определить, является ли та или иная стратегия оптимальной, а также найти решение игры, т.е. цену игры и множество оптимальных стратегий.
Начнем
с первого вопроса: как определить,
является ли некоторая стратегия
оптимальной или нет? Доказано, что
оптимальные стратегии игроков
обладают следующим свойством:
,
причем
цена игры
.
Удалось
также доказать следующее. Чтобы стратегии
и
были оптимальными необходимо и достаточно
выполнение следующих неравенств:
для
всех
.
Определим на примере для игры Морра, являются ли оптимальными следующие смешанные стратегии:
|
|
|
|
|
|
|
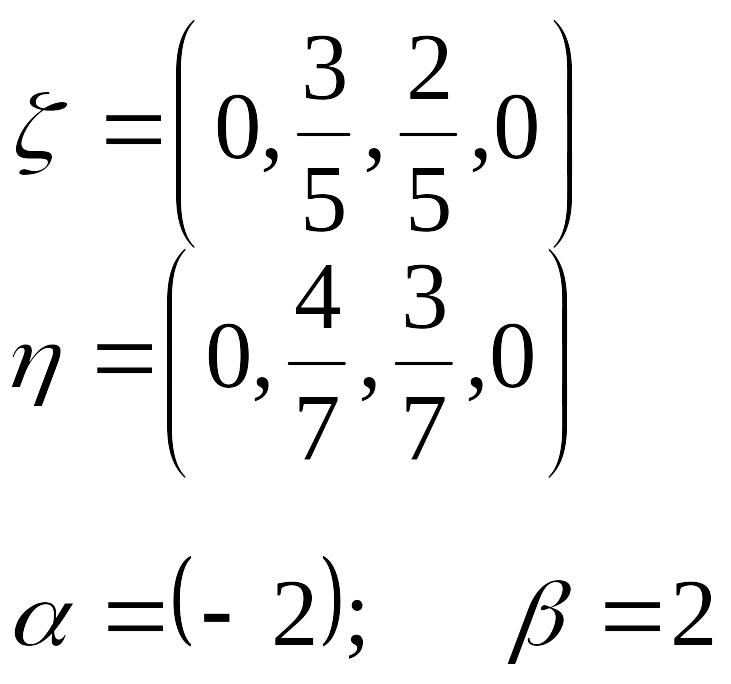
(1,1) |
(1,2) |
(2,1) |
(2,2) |
|||
|
(1,1) |
0 |
2 |
-3 |
0 |
-3 |
|
(1,2) |
-2 |
0 |
0 |
3 |
-2 |
|
(2,1) |
3 |
0 |
0 |
-4 |
-4 |
|
(2,2) |
0 |
-3 |
4 |
0 |
-3 |
|
3 |
2 |
4 |
0 |
|
|
Вначале
вычислим
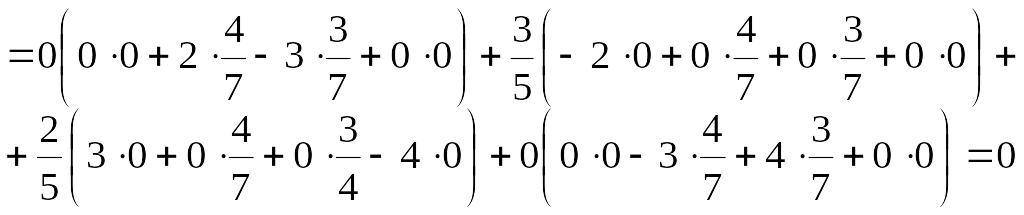
Далее,
приступим к проверке приведенных выше
неравенств. Если для некоторого значения
i
или j
неравенства не выполняются, то стратегии
ξ или η будут неоптимальными и проверку
на оптимальность можно останавливать.
Итак, вычисляем
и
:
=0,
=0,
=0,
=1/5.
Видно,
что неравенства справедливы для всех
индексов
,
следовательно, стратегии
и
являются оптимальными, а цена игры
L(ξ,η)=
.
Существует
ряд операций, которые можно выполнить
над платежными матрицами, не изменяя
множество оптимальных стратегий (это
бывает полезно при поиске решения игры).
Например, прибавление или умножение на
константу всех элементов матрицы
не изменит оптимальных значений, однако
цена игры изменяется на ν+Const
или ν*Const.
При перестановке строк или столбцов
матрицы
происходит перестановка составляющих
оптимального решения без изменения
цены игры. Можно также переставить
игроков, тогда элементы платежной
матрицы транспонируются с обратным
знаком.
Решение игры
Поиск решения игры (цены игры и оптимальных стратегий для 1-го и 2-го игроков) обычно начинается с исследования игры, т.е. с ответа на следующие вопросы:
Имеется или нет в игре седловая точка (в случае положительного ответа решение можно считать найденным, т.к. седловая точка указывает на цену игры и определяет оптимальные чистые стратегии игроков)?
Если седловая точка отсутствует, то пытаются упростить игру.
После возможного упрощения игры приступают к поиску решения.
На
чем основывается упрощение игры? – На
исключении заведомо невыгодных,
дублирующих или доминирующих
стратегий. Отметим также одно связанное
с этим важное понятие, которое используется
в некоторых методах решения игр. Речь
идет о понятии активной
стратегии.
Активной называется такая стратегия,
которая входит в состав оптимальной
смешанной стратегии с вероятностью
отличной от нуля, т.е.
или
:
.
Утверждение (без док-ва). Если один из игроков применяет свою оптимальную смешанную стратегию, то его выигрыш или проигрыш остается неизменным и равным цене игры, независимо от того, какую смешанную или чистую стратегию применяет другой игрок, если только этот игрок не выходит за рамки своих активных стратегий.
С другой стороны, необходимо понимать, что всегда наиболее выгодным является применение оптимальных стратегий. Использование игроком активных, но неоптимальных стратегий не приносит ущерба до тех пор, пока противник придерживается своей оптимальной стратегии, иначе он может «наказать» игрока, использующего активные, но неоптимальные стратегии.
Это очень важное положение используется при определении решения игры методом выделения подматриц, основанным на процедуре поиска активных стратегий. Метод заключается в декомпозиции исходной платежной матрицы на совокупность игр с простыми подматрицами, для которых нетрудно определить оптимальные решения, и в получении из них путем композиции решения исходной игры.
Известны и другие методы. Наиболее практичными из них являются геометрический метод, метод последовательных приближений и метод сведения игровой задачи к задаче линейного программирования. Прежде чем их рассматривать приведем два поучительных классических примера игровых задач с конфликтной ситуацией.
Дилемма узника. Игроками являются два узника, находящиеся в предварительном заключении по подозрению в совершении преступления. При отсутствии прямых улик возможность их осуждения в большой степени зависит от того, будут они говорить (Г) или молчать (М).
|
М |
Г |
М |
-1 |
-9 |
Г |
0 |
-5 |
Если оба сознаются, то получат срок 5 лет, учитывающий признание как смягчающее обстоятельство. Если же заговорит только один, а другой будет молчать, то заговоривший будет выпущен на свободу, а сохранивший молчание получит 9 лет. Эта конфликтная ситуация описывается приведенной выше матрицей игры. Ясно, что наиболее выгодной стратегией является молчание. Однако простое рассуждение показывает, что, не имея никаких контактов между собой и к тому же не очень доверяя друг другу, каждый из них, поразмышляв, придет к выводу, что нужно сознаваться и получить 5 лет, чем молчать и, возможно, получить 9 лет. Действительно, анализ с точки зрения теории антагонистических игр двух лиц с нулевой суммой, показывает, что в матрице игры существует СТ, она равна (-5) и соответствует стратегии (Г).
Золото пиратов. Конфликтные ситуации разнообразны, различны и способы их разрешения. Каждому приходилось принимать участие в переговорах. Часто переговоры связаны с дележом (доходов, ответственности, территории). Поэтому прежде чем делить, необходимо договориться о процедуре дележа. Рассмотрим две уже проработанных процедуры дележа, которые выглядят вполне демократичными и открытыми, но происходят в атмосфере взаимного недоверия. Пусть пираты делят золото (песок или слитки).
З
олотой
песок. Каждый
стремится получить свою справедливую
долю
.
Предположим вначале, что
.
Тогда лучшей считается стратегия
«дели-выбирай». Один делит на две части,
а другой выбирает любую из них.
Пусть
теперь в дележе участвуют три пирата
(
).
В этом случае первый пират выделяет
часть, на которую он претендует; и если
второй и третий одновременно согласны
с выбором первого, то он получает свою
долю и выбывает из дележа. Если не
согласны оба пирата, то право деления
передается другому пирату. Если же с
предложением первого пирата согласен
только один, то третьему участнику
дается право выделить из доли первого
свою часть, и он выбывает из дележа.
Деление 100 слитков. Иначе выглядит процедура деления золотых слитков. Сначала дележ проводит старший пират. Его предложение принимается, если с ним согласна хотя бы половина пиратов, включая его самого. Если с ним не согласится больше половины, то он выбывает из дележа, а право дележа передается второму по старшинству пирату и т.д. Итоги дележа при этом будут выглядеть следующим образом:
(младший пират понимает, что если он поддержит среднего пирата, то в итоге не получит ничего),
n=4 (99; 0; 1; 0) (рассуждение старшего пирата: надо предложить дележ, который был бы выгоден хотя бы одному пирату, а мне давал бы наибольшую долю)
n=5 (99; 0; 1; 0; 1) и т.д.
Исход неожиданный. Парадокс состоит в том, что процедура дележа демократична лишь с виду, однако слитки делятся далеко не поровну. Причина парадокса в том, взаимное недоверие не дает возможности для кооперации. При n=3 средний пират еще до дележа мог бы предложить младшему провалить предложение старшего пирата 99, 90, 1, и разделить слитки, например, пополам. Но откуда у младшего пирата возьмется уверенность в том, что средний пират, заняв место старшего, не присвоит себе все золото?