4.4. Марковские модели принятия решений

В данном разделе рассматриваются многостадийные задачи принятия решений с конечным числом состояний Sj(/ = I, ..., m) оптимизируемой счстемы S. Предполагается, что в дискретные моменты времени t_x, t₂, ... система переходит в новое состояние в соответствии с некоторой матри­цей переходных вероятностей:

р11 р12 … р1m

P= р21 р22 … р2m

… … … …

Рm1 pm2 … pmm

Элемент p_i} матрицы означает вероятность перехода системы из состоя­ния S/ в состояние Sj. Таким образом, строки матрицы соответствуют "старым", а столбцы — "новым" состояниям. Очевидно, сумма элементов любой строки матрицы равна 1.

Такой процесс поведения системы называется марковским, если вероят­ность перехода системы в любое возможное состояние в каждый момент времени определяется только ее состоянием в предыдущий момент вре­мени и не зависит от более ранней предыстории.

Многие практические ситуации могут быть описаны с помощью аппара­та марковских моделей. Рассмотрим конкретный пример.

Пример 4.3. Некоторая фирма занимается промышленной разработкой программного обеспечения для компьютерных систем. В начале каждого года она решает задачу замены оборудования, включающего техниче­ские и программные средства, используемые в производственном про­цессе и обеспечивающие необходимую технологическую среду разработ­ки. В зависимости от результатов экспертной оценки оборудования состояние фирмы (это система S) оценивается как "хорошее" (1), "удов­летворительное" (2) и "плохое" (3). Следовательно, система может нахо­диться в одном из трех указанных состояний. Матрица переходных веро­ятностей может иметь вид:

Здесь, например, число 0, 3 означает, что если система находилась в "хо­рошем" состоянии, то в следующий момент изменения состояния (сле­дующий момент анализа состояния фирмы) она окажется в "плохом" состоянии с данной вероятностью. В действительности изменение (ухуд­шение) состояния связано с процессом износа и устаревания оборудова­ния и технологических сред. Если матрица переходных вероятностей не меняется, то достаточно просто проанализировать весь жизненный цикл системы S.

Предположим, что в зависимости от состояний, в которых последова­тельно оказывается система, может быть вычислен доход, приносимый фирмой. Логично предположить, что доход за период /_/+,—/, зависит от уровня оснащенности фирмы современным оборудованием и технологи­ческим окружением, включая профессиональный уровень персонала, также требующий непрерывного повышения. В свою очередь, уровень оснащенности в значительной степени коррелирует с тем состоянием, в котором находилась фирма в начале рассматриваемого периода и в его конце. Если, например, в момент времени t_t система находилась в "хорошем" состоянии и в момент /,+, это состояние сохранилось, то, по-видимому, доход будет максимальным (конечно, при выполнении про­чих условий, связанных с наличием заказов, ситуации на рынке и т. д.).

Для моделирования этой ситуации можно матрице переходных вероятностей P поставить в соответствие матрицу доходов R:

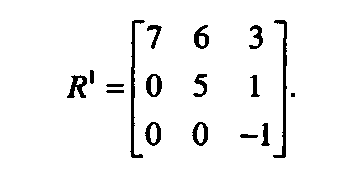
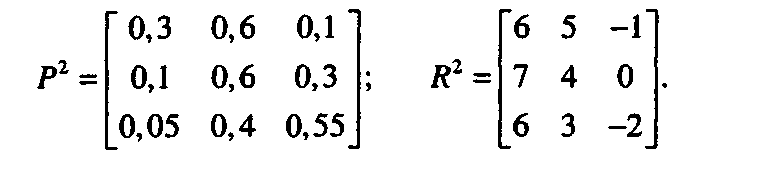
Здесь в матрице доходов мы учли затраты на реорганизацию и модифи­кацию. Например, элемент г,, матрицы /доказывается меньше соответ­ствующего элемента матрицы R^].

На каждом этапе мы можем принять решение не проводить модерниза­цию фирмы и иметь матрицы Р^[ и R¹ или принять решение о необходи­мых изменениях и получить матрицы Р², Л². Возникает проблема выбора или принятия решений с целью максимизации приносимого фирмой ожидаемого (речь идет о вероятностях!) дохода. Это многоэтапная зада­ча принятия решений, т. к. выбор осуществляется каждый раз в заданные дискретные моменты времени.

С привлечением уже рассмотренного примера обсудим основные момен­ты выбора оптимального решения. Предположим, что планирование

стратегии поведения фирмы осуществляется на конечный период време­ни. Покажем, что решение может быть основано на уже известном мето­де динамического программирования (метод Беллмана) в соответствии с общей концепцией анализа и оптимизации многошаговых задач (см. разд. 4.3).

Пусть период t_i+]—t_t соответствует одному году, а планирование прово­дится на трехлетний период. Для наглядности соответствующее дерево решений можно представить графически (рис. 4.11).

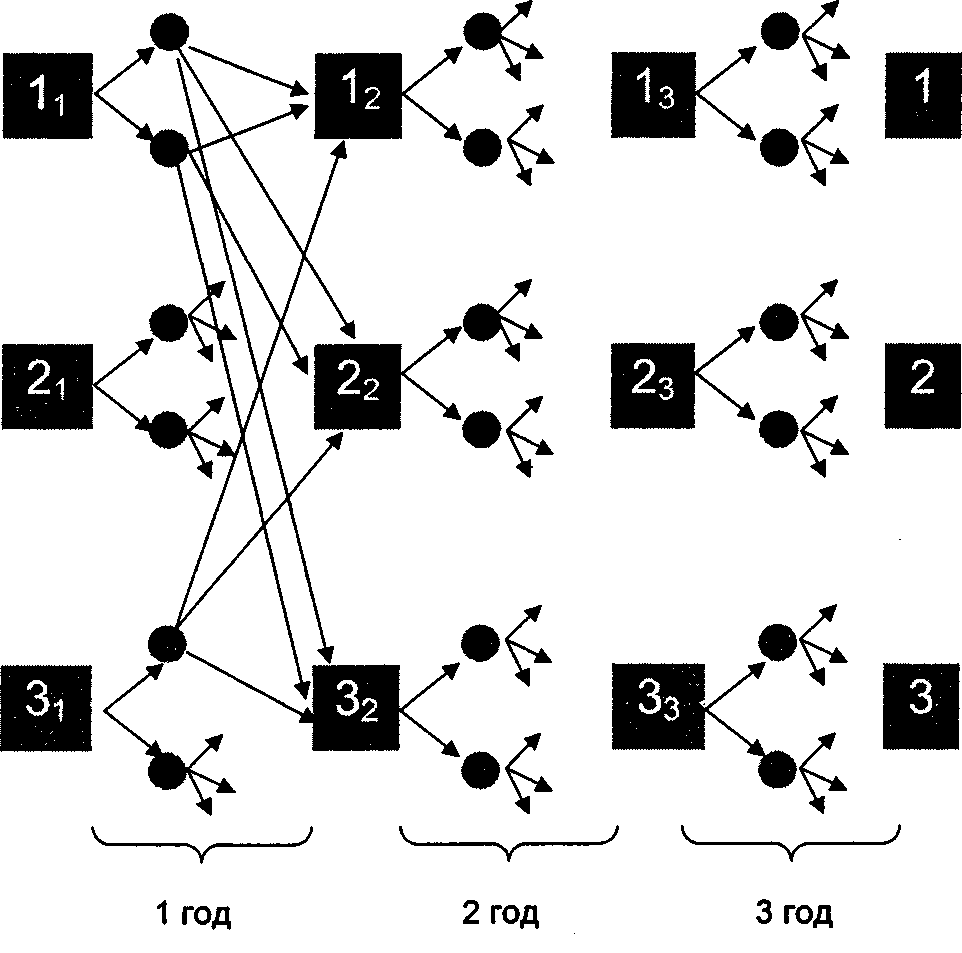
Рис. 4.11. Дерево решений

Как обычно, квадратики означают решающие вершины. Каждый квад­ратик соответствует определенному состоянию системы в определенный момент времени. Знак /, внутри квадрата означает, что в момент време-

ни у, j= 1, 2, 3 (номер этапа) система находится в состоянии /, /= 1, 2, 3 (соответственно, "хорошее", "удовлетворительное" или "плохое" состояние). Две стрелки, исходящие из каждой "решающей" вершины, соответствуют двум альтернативам на каждом этапе: х^ — проводить модернизацию (это верхняя стрелка, будем называть ее стрелкой или направлением 1) или х₂ — не проводить (это нижняя стрелка, будем называть ее стрелкой или направлением 2). Кружочки означают "случайные" вершины, пере­ход из которых осуществляется в соответствии с выбранной матрицей переходных вероятностей.

Следуя общему алгоритму динамического программирования, решаем задачу с конца. Двигаемся справа налево по решающим вершинам. Нач­нем с вершины 1₃. Тогда при принятии решения jc, (без модернизации) ожидаемый доход равен

При выборе х₂ (модернизация) имеем:

Число 5,3 больше, чем 4,7, поэтому если мы окажемся в вершине 1₃, то пойдем по направлению 1, а сама вершина помечается числом 5,3. Стрелка 1 также выделяется.

Далее переходим к вершине 2₃. Получаем значения двух доходов в зави­симости от принимаемых решений:

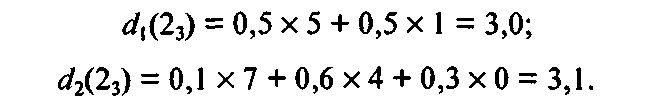
Вершина 2₃ помечается числом 3,1 и выделяется направление 2. Для вершины 3₃ получим:

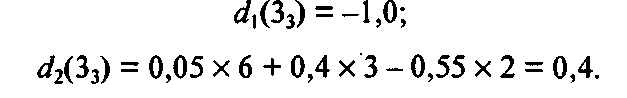
Вершина 3₃ помечается большим числом 0,4 и выделяется стрелка 2.

Полученные числа 5,3, 3,1, 0,4 характеризуют один акт изменения со­стояния и получаемый при этом локальный доход. Далее эти вычисления уже не повторяются, а значения этих локальных доходов потребуются в дальнейших расчетах.

Переходим теперь к началу второго года. Начнем с вершины 1₂. При вы­боре направления (решения) 1 имеем:

Здесь число 5,3 отражает локальный доход этапа (рассчитанный ранее), а остальные слагаемые характеризуют наилучший ожидаемый доход, по­лучаемый на оставшихся этапах. Для второго варианта решения для этой же вершины имеем:

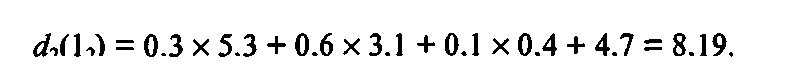
Число 8,19 больше, чем 8,03, поэтому вершину 1₂ помечаем числом 8,19 и выделяем стрелку 2.

Для вершин 2₂ и 3₂ проводим аналогичные расчеты:

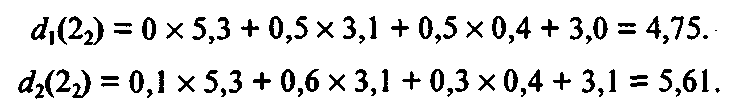
Выбираем число 5, 61 и выделяем стрелку 2. Далее имеем:

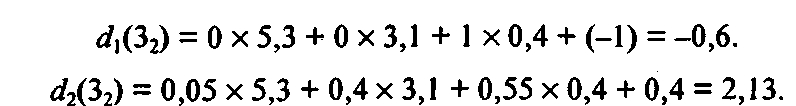
Для первого этапа аналогично получаем:

Теперь обратная процедура динамического программирования законче­на и, двигаясь от начала дерева решений к концу, можно "прочитать" оп­тимальное решение. А именно: числа 10,74, 7,92, 4,23 означают опти­мальный ожидаемый доход, если, соответственно, система находилась первоначально в состояниях 1, 2 и 3. Эти ожидаемые доходы достигают­ся, если мы всегда будем вести себя "оптимально", т. е. в соответствии с помеченными на дереве решений стрелками. В частности, в каком бы со­стоянии мы ни находились в начале первого года, целесообразно реше­ние, связанное с модернизацией оборудования. То же относится к началу второго года (все выделенные стрелки направлены "вниз"). И только ес­ли в начале третьего года мы окажемся в состоянии 1, нам нецелесооб­разно проводить модернизацию оборудования фирмы.

Поставленная задача решена.

Отметим, что в теории марковских процессов принятия решений рас­сматриваются также модели с бесконечным числом этапов. Эти и другие вопросы рассматриваются в учебной литературе [36].

БИМАТРИЧНЫЕ ИГРЫ

Предыдущие рассмотрения касались игр двух лиц, в которых ин­тересы игроков были прямо противоположны (антагонистические, или матричные, игры), а также позиционных игр, сводимых к ма­тричным. Однако ситуации, в которых интересы игроков хотя и не совпадают, но уже необязательно являются противоположными, встречаются значительно чаще.

Рассмотрим, например, конфликтную ситуацию, в которой каж­дый из двух участников имеет следующие возможности для выбора своей линии поведения:

игрок А — может выбрать любую из стратегий Ai,..., A_m, игрок В — любую из стратегий Z?i,..., В_п.

При этом всякий раз их совместный выбор оценивается вполне оп­ределенно:

если игрок А выбрал г-ю стратегию А;, а игрок В — к-ю стратегию Bk, то в итоге выигрыш игрока А будет равен некоторому числу а,^, а выигрыш игрока В — некоторому, вообще говоря, другому числу Ь^.

Иными словами, всякий раз каждый из игроков получает свой приз.

Последовательно перебирая все стратегии игрока А и все страте­гии игрока В, мы можем заполнить их выигрышами две таблицы:

				Вп
				#ln
				&in
				®тп
				tj-n
				■ bln
Ai		Ъа ■	Ык • •	Oin
Ат		Ът\ • •	®тк ■ ■	®тп

Первая из таблиц описывает выигрыш игрока А, а вторая — вы­игрыш игрока В. Обычно эти таблицы записывают в виде матриц:

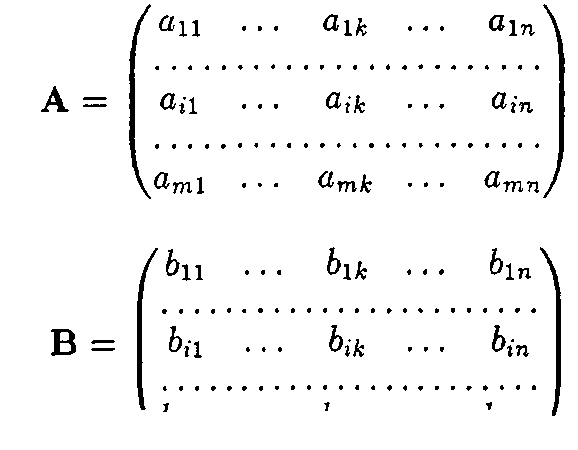
\0_т1 ' • ' ®тк • • ' ^тп/

Здесь А — платежная матрица игрока Л, а В — платежная ма­трица игрока В.

При выборе игроком А г'-й стратегии, а игроком В — fc-й страте­гии их выигрыши находятся в матрицах выплат на пересечении г-х строк и /г-х столбцов:

в матрице А это элемент а,-*, а в матрице В — элемент bik.

Таким образом, в случае, когда интересы игроков различны (но необязательно противоположны), получаются две платежные мат­рицы: одна — матрица выплат игроку Л, другая — матрица выплат игроку В. Поэтому совершенно естественно звучит название, которое обычно присваивается подобной игре, — биматричная.

Замечание. Рассмотренные ранее матричные игры, разумеется, можно отнести и к биматричным, где матрица выплат игроку В про­тивоположна матрице выплат игроку А:

bik = —o,ik

или

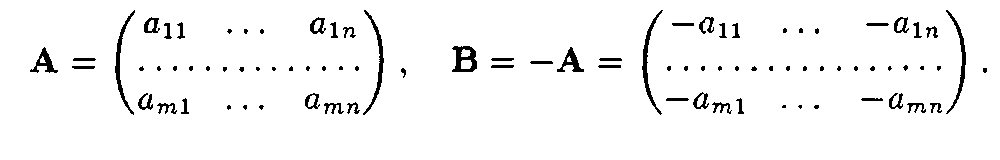
Тем не менее в общем случае биматричная игра — это игра с ненулевой суммой.

Нам кажется вполне естественным время от времени сопостав­лять наши рассмотрения с рассуждениями, приведенными ранее для матричных игр (особенно при попытках разрешения сходных про­блем). Подобные сопоставления часто оказываются одновременно и удобными и полезными. Конечно, класс биматричных игр значите­льно шире класса матричных (разнообразие новых моделируемых конфликтных ситуаций весьма заметно), а значит, неизбежно уве­личиваются и трудности, встающие на пути их успешного разреше­ния. Впрочем, мы надеемся, что часть этих трудностей мы сумеем преодолеть уже в настоящем издании.