Метод promethee

Метод получил свое название из аббревиатуры полного названия: Preference Ranking Organisation METHod for Enrichment Evaluations. В данном методе сравнения пар объектов i и l по каждому критерию используют функцию предпочтения H_j(d), где d – разность значений критериев двух объектов.

Пример пороговой функции предпочтения приведен на рис.2.5. Содержательно она отражает тот факт, что если разность несущественна, то объекты по критерию j эквивалентны. При превышении разности порогового значе­ния p_j между объектами устанавливается отношение предпочте­ния.

соответствует тому, что объект i предпочтительнее объекта l по k_j. означает, что имеет место отноше­ние безразличия.

В ышеприведенную функ­цию предпочтения следует рассматривать как одну из возможных для использова­ния в данном методе. Напри­мер, в методе ELECTRE при определении коэффициента согласия тоже использовалась функция предпочтения, если принять p_j =0 (j=1,...,m).

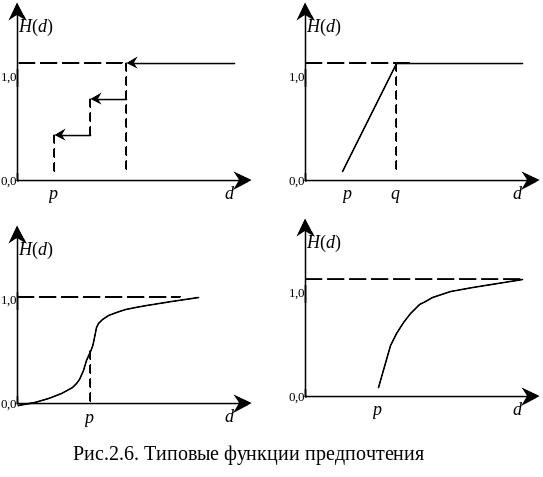
Можно использовать и другие функции предпочте­ния, которые позволяют оце­нить степень предпочтения пары объектов по j критерию непрерывной величиной, т.е H_j(d) меняется от нуля до единицы. Примеры таких функций приведены на рис.2.6.

Таким образом, ЛПР должно задать для каждого критерия функцию предпочтения H_j(d).

Для оценки предпочтения Вⁱ над В^l по всей совокупности критериев вводится индекс предпочтения "П_i,l", вычисляемый по формуле: , где W_j — веса критериев 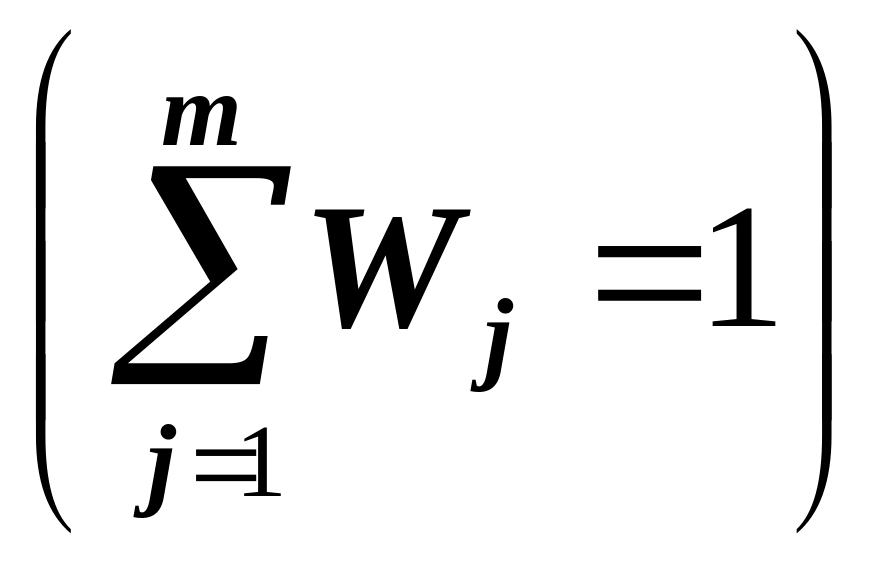, отражающие их важность.

Матрицу индексов предпочтения ║П_i,l║ можно представить в виде ориентированного графа предложений со взвешенными дугами, причем между каждой парой вершин устанавливаются две дуги с весами П_i,l и П_l,i.

На следующем этапе метода для каждого объекта определя­ются:

а) коэффициент предпочтения путем суммирования индексов предпочтения по всем выходящим дугам:

;

б) коэффициент обратного предпочтения путем суммирования индексов предпочтения по всем входящим дугам:

.

Вычисляемые коэффициенты и являются информационной базой для ранжирования объектов и использу­ются по-разному в модификациях метода.

Модификация 1 (PROMETHEE 1)

В этой модификации формируются бинарные отношения между каждой парой объектов:

, если ( и ) или ( и ), или ( и );

(безразличны), если и ;

Вⁱ не сравним с В^l во всех других случаях.

Множество установленных бинарных отношений предпочте­ний отражает частичный порядок объектов.

Модификация 2 (PROMETHEE 2)

Данная модификация позволяет упорядочить объекты. Для этого вычисляется один коэффициент , характеризую­щий предпочтение Вⁱ по следующей формуле: .

По значениям объекты упорядочиваются.

Следует отметить, что не всегда предпочтительнее является модификация 2, так как больше информации о предпочтении объектов получает ЛПР, анализируя попарные отношения предпочтения. Так как этот метод является эвристическим, то получаемые результаты являются дополнительной информацией для ЛПР и ему лучше иметь исходную информацию в виде множества бинарных отношений, чем агрегированную в модификации 2.

Результаты решения задач с использованием описанных методов показывают, что использование метода PROMETHEE позволяет получить более устойчивые решения по сравнению с методом ELECTRE.