Метод смещенного идеала

Метод предназначен для выделения одного или подмно­жества наиболее предпочтительных объектов. Характерными особенностями метода являются:

1. наличие процедуры формирования "идеального" объекта (В⁺), служащего своего рода целью, к которой надо стремиться. Такой “идеал”, как правило, не достижим и не существует реально, но его полезно иметь для понимания ЛПР своих целей;

2. на каждой итерации производится исключение объектов, не претендующих на наиболее предпочтительные, т.е. не выделяются "лучшие" объекты, а исключаются "худшие".

В общем виде алгоритм метода следующий (рис 2.2): сна­чала исключаются доминируемые объекты, так как среди них не может быть наиболее предпочтительного.

Формируется “идеальный” объект В⁺⁽¹⁾ из наиболее предпо­чтительных значений критериев и “антиидеальный” из наименее предпочтительных значений. Определяются расстояния от объектов из исходного множества до “антиидеала”, на основании которых выделяются “худшие” объекты. Среди таких объектов, как правило, есть объекты, имеющие одно наиболее предпочти­тельное значение (объекты В¹ и В⁶ на рис 2.2).

После исключения “худших” объектов вновь переходим к э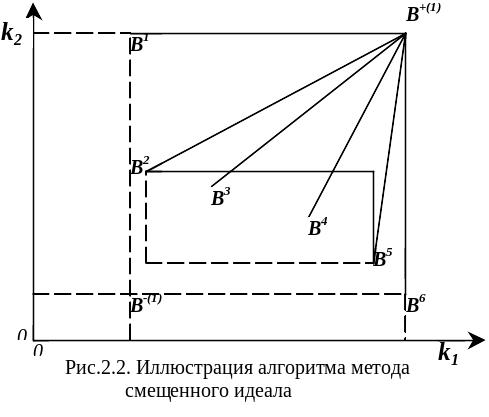 тапу формирования “идеала”, и он изменяется (на рисунке это В⁺⁽²⁾), приближаясь к реаль­ным объектам.

Процедура заканчивается, когда останется небольшое число объектов, которые и считаются наиболее предпо­чтительными.

С

0

ледует отметить, что при сравнении реально существу­ющих объектов с “идеалом” у ЛПР возникает неудовлетво­ренность, вызванная недо­ступностью сформированного “идеала”. Эту неудовлетворен­ность называют конфликтом перед решением.

После выбора наиболее предпочтительного объекта у ЛПР возникает неудовлетворенность, вызванная тем фактом, что выбран именно данный объект, а не другой. Такую неудовлет­воренность называют конфликтом после решения.

На первых итерациях метода превалирует конфликт перед решением. На последующих итерациях “идеал” приближается к реальным объектам и конфликт перед решением уменьшает­ся. Однако конфликт после решения может увеличиваться. Это свидетельствует о недостаточной изученности ЛПР решаемой задачи.

Рассмотрим подробно алгоритм метода, блок-схема которого приведена на рис.2.3.

Пусть исходное множество объектов включает п объектов. Все критерии k_j (j=l,…,m) измеряются по шкале интервалов или отношений.

На первом этапе формируется “идеальный” объект , где – максимальное по предпочтению значение критерия среди всех объектов, т.е. , если предпочтение объекта возрастает при увеличении k_j, или , если предпочтение объекта возрастает при уменьшении критерия. Если “идеал” принадле­жит множеству объектов, то он и будет наиболее предпо­чтительным. Но так как МКЗ обычно решается на множестве эффективных объектов, то “идеальный” объект не будет принад­лежать исходному множеству.

На этом же этапе формируется “наихудший” объект из наименее предпочтительных значений.

На втором этапе осуществляется переход от физических единиц измерения критериев к относительным в соответствии с выражением:

. (2.1)

В относительных единицах все критерии будут изменяться в интервале [0;1], при этом, чем меньше , тем ближе объект по критерию k_j к “антиидеальному”.

Первые два этапа выполняются автоматически без участия ЛПР. На третьем этапе ЛПР, исходя из своих суждений о важности критериев, задаёт веса критериев W_j ( j = 1,...,m).

В случае затруднения ЛПР может воспользоваться информационным подходом к определению важности критериев, На следующем, четвёртом, этапе рассчитываются расстоя­ния объектов до “антиидеала”. В качестве метрики используется следующее выражение:

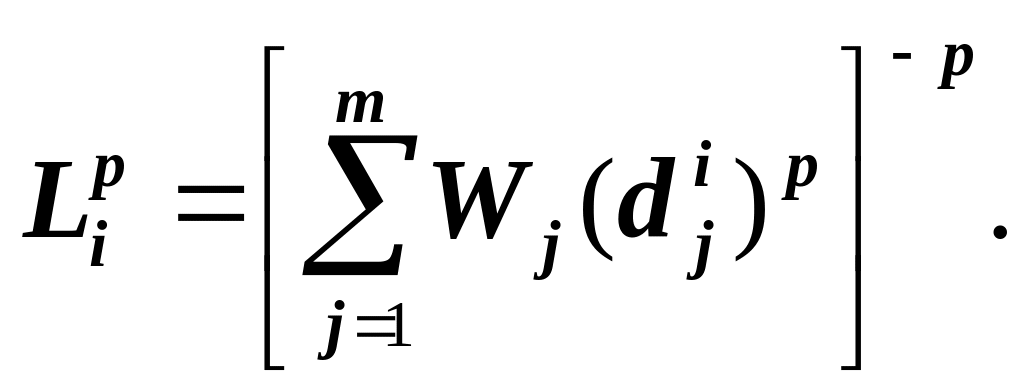(2.2)

Используя в (2.2) разные р, можно получить различные метрики. Так, при р=1, получим аддитивный оператор, а при (2.2) переходит в . Чем больше значение , тем дальше объект от “антиидеала” и ближе к “идеальному”.

С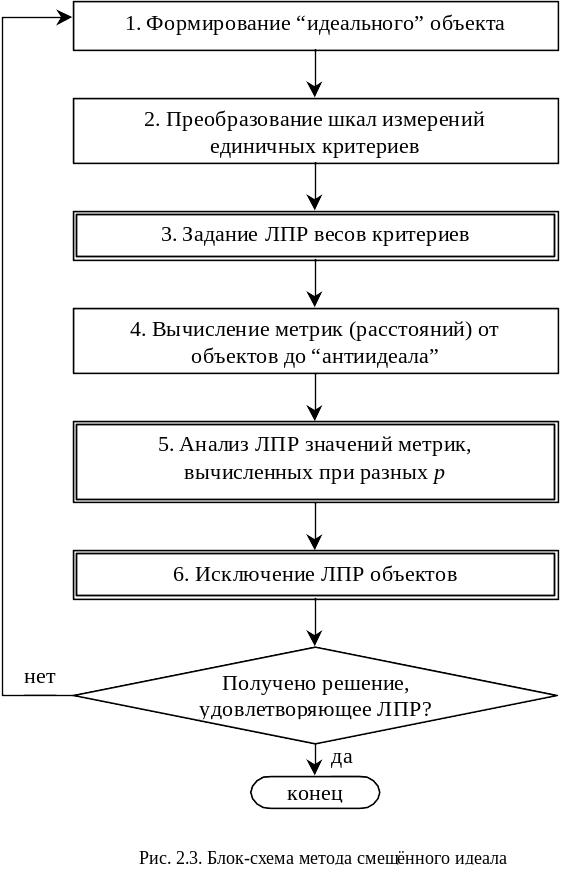 ледует отметить, что в качестве метрики для сравнения объекта с “идеальным” можно использовать и другие операторы агрегирования.

На следующем, пятом, этапе, задавая различные значения р, ЛПР определяет разные метрики для сравнения с “идеаль­ным”. При каждом р, т.е. для каждой метрики, все объекты упорядочиваются по близости к “идеалу” по величине . ЛПР в диалоге, изменяя p, исследует влияние различных метрик на упорядочение объектов.

Далее, на шестом этапе ЛПР принимает решение об исключении объектов, не претендующих на наиболее предпо­чтительный. Очевидно, что это те объекты, которые при различных метриках (разных р) находятся в конце упорядо­ченных рядов. Действительно, если независимо от выбранной метрики объект далек от “идеала”, то есть все основания исключить его.

После исключения объектов начинается следующая итера­ция с формирования “идеального” объекта уже на оставшемся подмножестве объектов.

Заканчивается процедура, когда после очередного исключе­ния осталось небольшое число объектов, которые и будут наиболее предпочтительными.

Следует отметить, что на каждой итерации целесообразно анализировать разброс критериев. Дело в том, что среди исключаемых объектов, как правило, есть объекты, включаю­щие максимальные и минимальные значения критериев. Тем самым на каждой итерации уменьшается область изменения критериев и, значит, существенно изменяется их разброс. Тогда, используя информационный подход, можно выделить неинфор­мативные критерии и в целях упрощения задачи исключить такие критерии.

В заключение отметим, что данный метод наиболее эффективен при больших размерностях задачи.