Интерактивные методы решения мкз

Интерактивные методы ориентированы на решение МКЗ, в которых требуется выделить наиболее предпочтительный объект (решение). В некоторых методах удается упорядочить объекты по предпочтению.

В основу каждого метода положен определенный подход к выбору наиболее предпочтительного объекта. В большинстве случаев такие эвристические подходы создаются на основе анализа и решения практических задач. Так как многокри­териальные задачи часто встречаются в практике и, значит, их постановок большое число, то и интерактивных методов значи­тельное количество.

В данном разделе рассмотрены различные по своим подходам методы. Первые два метода: метод уступок и метод смещенного идеала относятся к разным группам методов. Последующие три метода относятся к группе методов, позволяющих устанавливать бинарные отношения между объектами (outranking). В этих методах между объектами устанавливаются отношения: предпочтения (), безразличия (~) или несравнимости (N). Одним из первых методов этой группы был метод ELECTRE, получивший свое развитие в методе PROMETHEE. К этой же группе относится и метод ORESTE, но он существенно отличается от вышеперечисленных методов. Изложенные в данном разделе методы дают представление о многообразии интерактивных методов решения МКЗ.

Метод уступок

Данный метод позволяет выделить наиболее предпочти­тельный объект из конечного исходного множества.

Основная идея метода заключается в поэтапном исключе­нии доминируемых объектов. Для установления доминирования между конкурирующими по двум критериям объектами используются коэффициенты замещения критериев. Блок-схема метода приведена на рис.2.1. Рассмотрим метод на примере.

Пусть стоит задача выбора варианта квартиры по трём критериям: k₁ – цена (тыс.$), k₂ – площадь (м²), k₃ – расположение дома от метро (мин ходьбы до метро). Опреде­лим характер изменения критериев: предпочтение вариантов возрастает при уменьшении k₁, k₃ и при увеличении k₂. Альтернативные варианты приведены в табл.2.1.

Таблица 2.1

Пример выбора варианта квартиры

Варианты квартир	k1, тыс.$	k2, м2	k3, мин
В1	24	27	8
В2	30	30	10
В3	34	32	16
В4	32	32	12
В5	26	30	16

На первом этапе выделим доминируемые варианты. Среди пяти исходных В⁴ доминирует В³, поэтому вариант 3 исключа­ем. Оставшиеся варианты конкурируют между собой (оптималь­ны по Парето).

На втором этапе зададим коэффициент замещения второго критерия первым. В данном примере ЛПР должно ответить на вопрос: сколько тыс.$ оно готово заплатить за каждый дополни­тельный квадратный метр площади. Пусть

,

т.е. на столько по критерию k₁ он уступает при сравнении вариантов по критерию k₂.

С учетом заданного коэффициента замещения Z_2,1 сравним варианты В¹ и В².

По критерию k₁ вариант 1 предпочтительнее на б тыс.$, а по критерию k₂, вариант 2 предпочтительнее на .

Таким образом с учетом Z_2,1 = 1 тыс.$ по критериям k₁ и k₂ вариант 1 предпочтительнее В², так как . Поскольку по критерию k₃ вариант 1 также предпочтительнее В², то В¹ доминирует В² и значит В² должен быть исключен.

З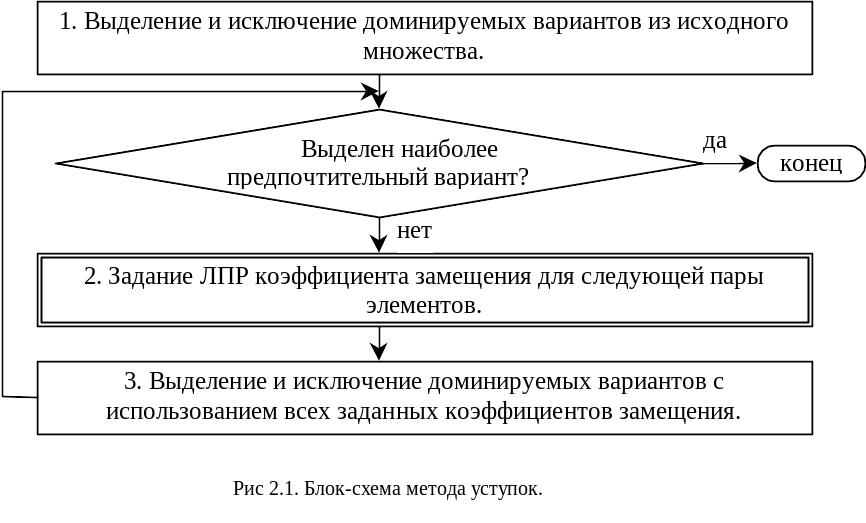 десь и далее во всех блок-схемах интерактивных методов двойными контурными линиями выделены блоки, выполняе­мые с участием ЛПР. При сравнении В¹ и В⁴ получим:

. С учетом значений k₃ вариант 1 доминирует В⁴.

Сравнивая В¹ и В⁵, определим

Значит, В⁵ предпочтительнее В¹ по критериям k₁ и k₂, а с учётом k₃ получим, что эти два варианта конкурируют между собой.

После исключения доминируемых вариантов на основе коэффициента замещения Z_2,1 остались два варианта В¹ и В⁵.

Зададим коэффициент замещения третьего критерия первым. Пусть ЛПР готово уступить за каждую минуту (расстояние до метро) 100 $, т.е.

Сравнивая варианты В¹ и В⁵, получим

Значит В⁵ предпочтительнее В¹. Однако, надо иметь в виду, что вывод о предпочтительности В⁵ неустойчив. Действи­тельно, если коэффициент замещения Z_2,1 принять равным 0,15 тыс.$, получим, что В¹ предпочтительнее В⁵.

Поэтому для большей уверенности при выборе вариантов следует ввести дополнительные критерии.

Необходимо отметить, что при использовании метода уступок важно производить исследование устойчивости результа­та от задаваемых коэффициентов замещения.

Порядок, в котором вводятся в алгоритм коэффициенты замещения, не влияет на итоговый результат выделения наиболее предпочтительного варианта, т.е., если бы в примере ввести сначала Z_3,1, а потом Z_2,1, всё равно В⁵ будет наилуч­шим.

В заключение отметим особенности метода уступок:

1. метод позволяет выделять наиболее предпочтительные варианты;

2. отсутствуют процедуры перехода к относительным единицам (они не требуются);

3. агрегирование критериев осуществляется через коэффици­енты замещения критериев;

4. результаты выделения наиболее предпочтительного варианта часто неустойчивы к коэффициентам замещения. Поэтому особое внимание следует уделять исследованию резуль­татов на устойчивость.