Многокритериальные решения: модели, оценка альтернатив, выбор решений

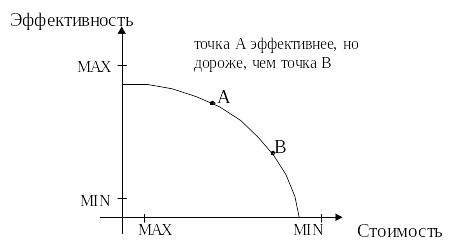
Одним из первых подходов к ПР при 2-х критериях является метод «Стоимость - эффективность» (разработан в конце 50-х годов в США для задачи достаточности системы ракетно-ядерного нападения для преодоления защиты потенциального противника). Метод включает три этапа: построить модель эффективности; построить модель стоимости; синтез оценок стоимости и эффективности. Модели строятся на базе фактических данных и надежной статистики. Руководители определяют предельные значения отношения стоимость/эффективность. Затем на этапе синтеза оценок один из критериев становится ограничением. Иными словами, необходимо:

1. Выбрать самую дешевую альтернативу для фиксированной эффективности;

2. Выбрать вариант с наибольшей эффективностью для фиксированной стоимости;

3. Построить множество Эджворта – Парето (рис.) и, сравнивая варианты на этом множестве, сделать окончательный выбор.

Г.Саймон и А.Ньюэлл (1958г.), пытаясь подчеркнуть особенности задач ПР, предложили их классификацию на хорошо и слабоструктурированные проблемы, т.е. проблемы, в которых все существенные зависимости можно выразить количественно и смешанные проблемы, которые в большинстве своем содержат малоизвестные качественные элементы (например, выбор профессии, места работы и т.п.).

Появление многокритериальных задач привело к тому, что основой выработки решений стали предпочтения ЛПР. Решение становится субъективным, хотя в его процессе используются объективные модели. Характерной особенностью многокритериальных задач является то, что одновременно рассматриваются два множества: пространство критериев и пространство переменных.

Рассмотрим пример простой задачи с 2 критериями и 2 переменными.

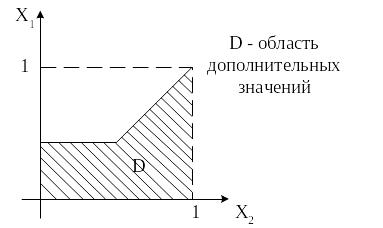
Из множества переменных, описывающих экономическую систему государства выберем две: х₁ - увеличение объема денежной массы; х₂ – увеличение количества рабочих мест.

Предположим, что определенное число рабочих мест можно создать без увеличения денежной массы. После превышения некоторого порога увеличение мест происходит пропорционально увеличению денежной массы (рис. D – заштрихованная область допустимых значений х₁, х₂ € [0, 1]).

Введем два критерия: - уменьшение безработицы (%) и увеличение ВНП (%) соответственно. При одном критерии решение очевидно. Пусть

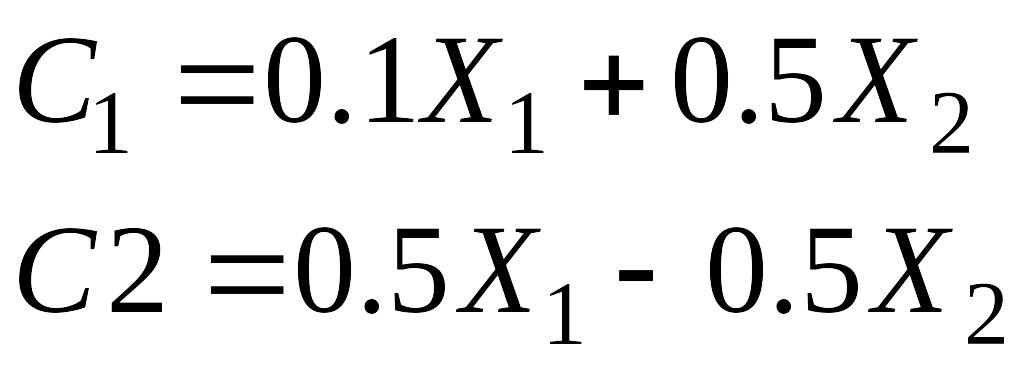, это позволяет построить достижимую область изменения значений критериев S (рис.) при изменении переменных.

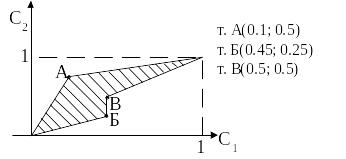
Отметим, что область S появляется только в многокритериальных задачах, для которых возникла идея построения множества Э-П и организации работы ЛПР на этом множестве. Из современных исследований в этом направлении необходимо выделить два подхода. Первый связан с визуализацией множества Э-П (метод достижимых целей). Другой подход характерен для деятельности конструктора, когда ему предъявляются решения из множества Э-П для поиска новых эффективных решений.

Теперь, когда основные трудности для ЛПР стали ясны, можно сформулировать многокритериальную задачу линейного программирования.

Дано: D – область допустимых значений переменных определяемая совокупностью линейных равенств и неравенств; C_i – критерии качества решения, линейно связанные с переменными х_i :

, где j=1,2,…n, c_ij –числовые коэффициенты

Требуется: найти решение , при котором достигаются наиболее приемлемые значения по всем критериям или экстремум априори неизвестной функции полезности ЛПР.

Эта задача решается с помощью человеко-машинных процедур (ЧМП).

ЧМП включают в себя фазу компьютерных расчетов и фазу анализа решений ЛПР. Различные ЧМП отличаются друг от друга способом выполнения каждой из фаз. Наибольшую трудность вызывает получение информации по результатам анализа от ЛПР. Естественно стремление получить эту информацию сразу и быстро устранить многокритериальность. Этот подход был реализован путем объединения многих критериев в один с помощью весовых коэффициентов важности критериев по формуле:

вес го критерия, i=1,2,…N.

Задача сводится к оперативному выяснению у ЛПР этих весов . Если ЛПР затрудняется, то он назначает первоначальные веса, а затем их корректирует.

В общем, существует следующая классификация ЧМП, основанная на информации, получаемой от ЛПР на фазе анализа:

1. Прямые методы. ЛПР непосредственно назначает веса критериев и корректирует их;

2. Методы оценки векторов. Задача ЛПР состоит в сравнении многокритериальных решений;

3. Методы поиска удовлетворительных решений. Требуют от ЛПР наложения ограничений на значения критериев и область достижимых значений.

Наиболее известным прямым методом является процедура SIGMOP. В ней ЛПР пытается найти решение путем назначения весов критериев и уровней допустимых значений по всем критериям одновременно: С_i ≥l_i. ЛПР задает w_i и l_i , компьютер определяет новую область D допустимых значений переменных и находит значение С_ГЛ, а также всех отдельных критериев. Если некоторый критерий не удовлетворяет начальному значению, то ЛПР меняет веса до тех пор пока процедура не даст приемлемого решения. Процедура применима для 2-3 критериев.

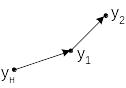
Наиболее известная процедура оценки векторов (метод Дайера-Джиофриона) начинается в выбора произвольной точки в пространстве критериев. ЛПР определяет градиент глобальной целевой функции: первый критерий считается опорным, берется небольшое изменение опорного критерия в сторону улучшения, ЛПР задается вопрос о том, какое изменение по другому критерию эквивалентно изменению опорного критерия, затем вдоль выбранного направления делается шаг и получаются новые значения критериев (рис.). Если новое решение (Y₁) лучше начального Y_н, то вычисляется решение Y₂ и т.д.

Примером ЧМП поиска удовлетворительных решений является STEM – метод. Вначале производится оптимизация по каждому критерию, а значения всех остальных критериев заносятся в отдельную таблицу размером (N, N):

Критерий	С1	С2	…
С1	1	с12	…
С2	c21	1	…
…	…	…	1

В таблице С_jⁱ – значение i-го критерия при оптимизации по j-му критерию. Ясно, что диагональные элементы равны 1, остальные – меньше 1. В таблице представлена ценная информация. Если значения двух столбцов близки, то два критерия сильно зависимы. Можно выявить противоречивые критерии: высокая оценка по одному сопровождается низкой оценкой по другому.

Затем вычисляются индексы критериев. Пусть – среднее значение, взятое по всем элементам – го столбца (кроме единицы). Тогда индекс -го критерия вычисляется из соотношения: .

Наконец, производится оптимизация по глобальному критерию

.

Найденное решение предъявляется ЛПР.

Рассмотрим классический пример применения метода STEM: как управлять персоналом, впервые предложенный французской консультативной фирмой SEMA.

Ставилась цель проверить стратегию приема на работу и повышения в должности через два, три и четыре года.

В качестве переменных использовалось количество сотрудников, назначенных на различные должности в определенные периоды времени. Использовались четыре линейных критерия: SA – общее удовлетворение кадров, EF – фактическая эффективность работы кадров, ER – стоимость приема на работу дополнительных сотрудников, EC – стоимость нехватки кадров.

В основу модели были положены зависимости:

• Эффективность работы сотрудников линейно зависит от отношения оценки его возможностей к оценке требований , предъявляемых должностью к сотруднику;

• Удовлетворение сотрудника должностью сначала растет до максимума, а затем уменьшается до первоначального значения в зависимости от отношения Q к t.

С математической точки зрения это была задача ЛП с 4 критериями, 350 переменными и 200 ограничениями. Для решения был использован метод STЕM. Была получена таблица, свидетельствующая о сильной зависимости критериев, определены индексы критериев, оптимизация по глобальному критерию и, наконец, диалог с ЛПР. В результате руководитель выбрал вектор при ЕС > -800 как обеспечивающий приемлемый компромисс между повышением качества по критерию ЕС и понижением качества по критериям SA и EF. Зная сильную взаимозависимость критериев SA и EF, руководитель выбрал решение, соответствующее максимуму EF, как окончательное: SA=0,76; EF=0,8; ER=-1500; EC=-800.

Критерий	SA	EF	ER	EC
SA	1	0,875	0,275	0,8
EF	0,86	1	0,09	0,765
ER	0,131	0,149	1	0,4
EC	0,442	0,45	0,733	1