Классические критерии пр.

К классическим относят три критерия: минимаксный (ММ), Байеса-Лапласа (BL), Сэвиджа (S). Рассмотрим их подробнее.

1. Критерий минимакса (ММ)

ММ-критерий является критерием крайнего пессимизма, он использует оценочную функцию вида:

.

Правило выбора решения по ММ-критерию следующее:

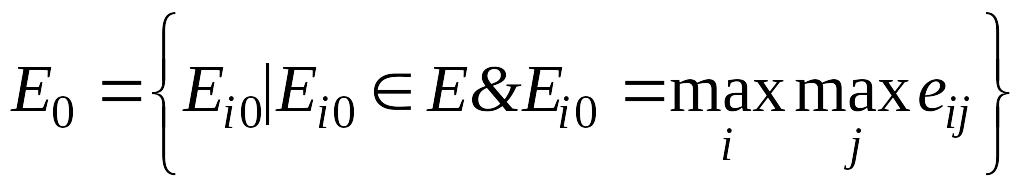, иными словами,

исходная матрица дополняется столбцом, состоящим из минимальных элементов каждой строки, т.е. , далее среди них выбирается максимальный элемент и, если их несколько, они образуют множество оптимальных по ММ-критерию решений .

Выбранные решения полностью исключают риск. Это означает, что ЛПР не может на практике столкнуться с худшим результатом, чем Z_мм при любых условиях . Это свойство позволяет считать ММ-критерий фундаментальным, особенно для технических задач, хотя и стоит определенных потерь.

Пусть, например, дана матрица выигрыша:

	F1	F2
E1	1	100
E2	1,1	1,1

Более выгодным представляется решение Е₁, однако по ММ-критерию оптимальным будет решение E₂, что становится совсем невыгодным, если состояние F₂ будет встречаться чаще, чем F₁, а решение реализуется многократно.

Практические рекомендации по применению ММ-критерия:

1. о вероятностях состояний заранее ничего не известно;

2. с возможностью появления отдельных состояний надо считаться;

3. решение реализуется однократно или небольшое число раз;

4. необходимо исключить какой бы то ни было риск, т.е. ни при каких состояниях не допускается результат худший, чем .

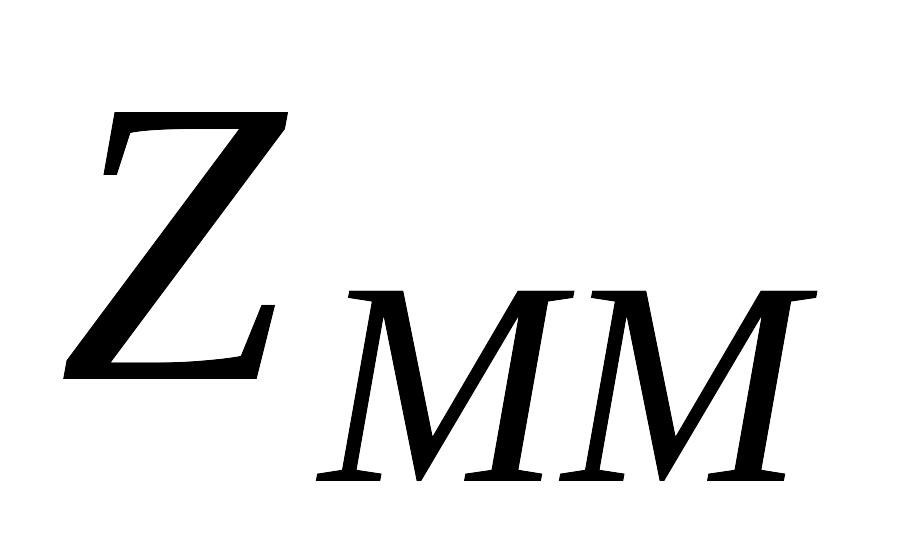2. Критерий Байеса-Лапласа (BL)

Критерий BL учитывает вероятность отдельных состояний .

Тогда оценочная функция BL имеет вид:

.

Правило выбора решения по BL-критерию следующее:

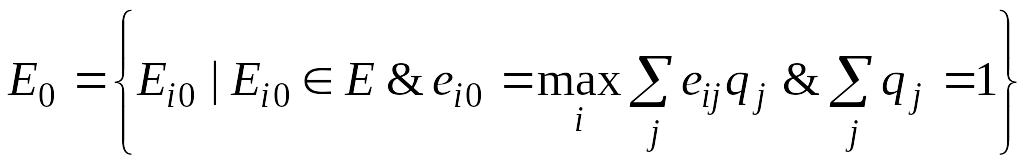, т.е.

исходная матрица дополняется столбцом, содержащим математическое ожидание элементов каждой строки, т.е. , далее среди них выбирается максимальный элемент и, если их несколько, они образуют множество оптимальных по BL-критерию решений.

Рекомендации по применению BL:

1. вероятности известны и не зависят от времени;

2. решение реализуется многократно;

3. для малого числа реализаций решения допускается некоторый риск.

Позиция ЛПР, применяющего BL, оптимистичнее, чем в случае с ММ, но она предполагает больший уровень информированности о ситуации и многократность реализации решений.

3. Критерий Сэвиджа (S)

От исходной матрицы переходят к матрице , где .

Затем определяется ,

формируется оценочная функция

и строится множество оптимальных по Сэвиджу вариантов решения

Величину можно интерпретировать как максимальный дополнительный выигрыш, который получается, если в состоянии вместо решения выбрать другое решение, оптимальное для состояния . Однако на практике величину интерпретируют как потери (штрафы), которые необходимо минимизировать. Рекомендации по применению S-критерия те же, что и для ММ.

Производные критерии

1. Критерий Гурвица (HW)

HW – это попытка занять компромиссную уравновешенную позицию между крайним оптимизмом и крайним пессимизмом.

, где

– весовой множитель Гурвица.

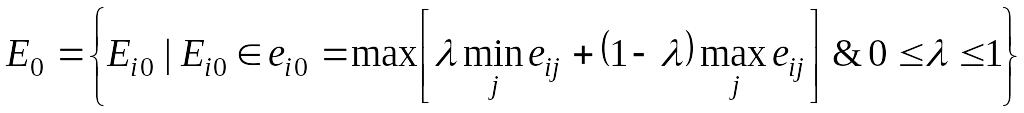
В технических задачах проблема выбора также трудна, как и вообще проблема выбора какого-либо критерия. Чаще берут . Бывает, что для приглянувшегося решения подбирается множитель .

Следующий контрпример показывает, что несмотря на вполне уравновешенную позицию по HW-критерию, можно прийти к нерациональному решению:

	F1	F2	…	Fn-1	Fn
Е1	10000	1	…	1	1
Е2	9999	9999	…	9999	0,999

Видно, что решение Е₂ является более предпочтительным, однако по Гурвицу при любом множителе оптимальным всегда будет решение Е₁.

Рекомендации по применению HW:

1. о вероятностях состояний природы ничего неизвестно;

2. с появлением отдельного состояния ЛПР должно считаться;

3. реализуется лишь малое число решений;

4. допускается некоторый риск.

2. Критерий Ходжа-Лемана (HL)

Этот критерий опирается одновременно на два классических критерия (BL и ММ). Вводится параметр, выражающий степень доверия к используемому распределению вероятностей q_ij, причем .

Если это доверие велико, то акцентируется BL-критерий делается на критерий BL, иначе, если невысок, то акцентируется внимание на ММ.

Оценочная функция , где решение .

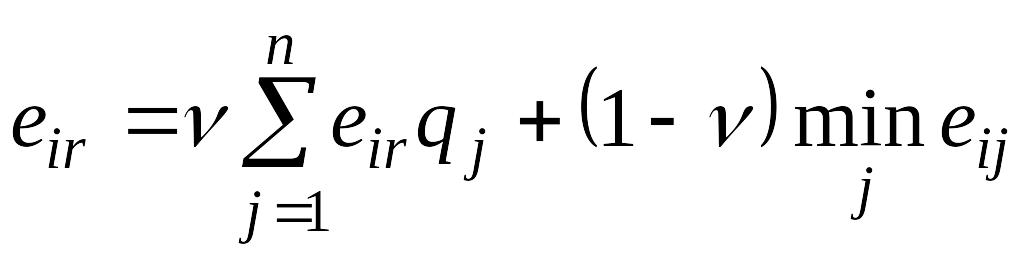Тогда оптимальное по HL множество решений

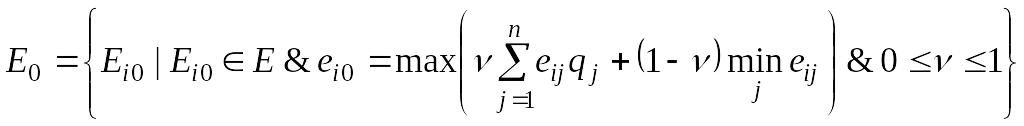
Очевидно, что HL при (абсолютное доверие) превращается в BL, а при в ММ. Выбор параметра субъективен. Число реализаций решения во внимание не принимается, поэтому рекомендации по применению HL-критерия таковы:

1. точные вероятности неизвестны, но некоторые предположения о значении есть;

2. предполагается, что решение принимается бесконечное число раз, если это не так, то допускается некоторый риск.

3. Критерий Гермейера (G)

Критерий Гермейера обладает эластичностью, он ориентирован на решения, которые не считаются заведомо худшими, чем другие. Он применяется для матрицы потерь, т.е. е_ij <0:

; где ;

.

Критерий Гермейера применим и в том случае, если некоторые элементы исходной матрицы . Для этого выбирается константа и путем прибавления ее ко всем элементам матрица приводится к отрицательному виду.

G-критерий является обобщением ММ-критерия. Это видно для случая равномерного распределения, когда все .

Рекомендации по применению:

1. известны вероятности ;

2. с появлением отдельных состояний необходимо считаться;

3. допускается некоторый риск.

4. решение может реализовываться один или много раз.

4. Критерий BL(ММ)

Критерий является составным, исходным в нем является BL-критерий. Предполагается, что распределение вероятностей является эмпирическим и поэтому известно не очень точно. Поэтому для применения критерия BL(ММ) вначале ищется опорное решение, получаемое по ММ:

, где и – это значения индексов, соответствующие решениям, оптимальным по ММ.

Далее выбирается уровень допустимого риска и на его основе устанавливается некоторое множество согласия, являющееся подмножеством индексов I={i}={1, 2,…,m}, обозначающих решение:

.

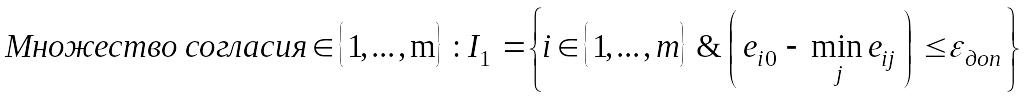Здесь величина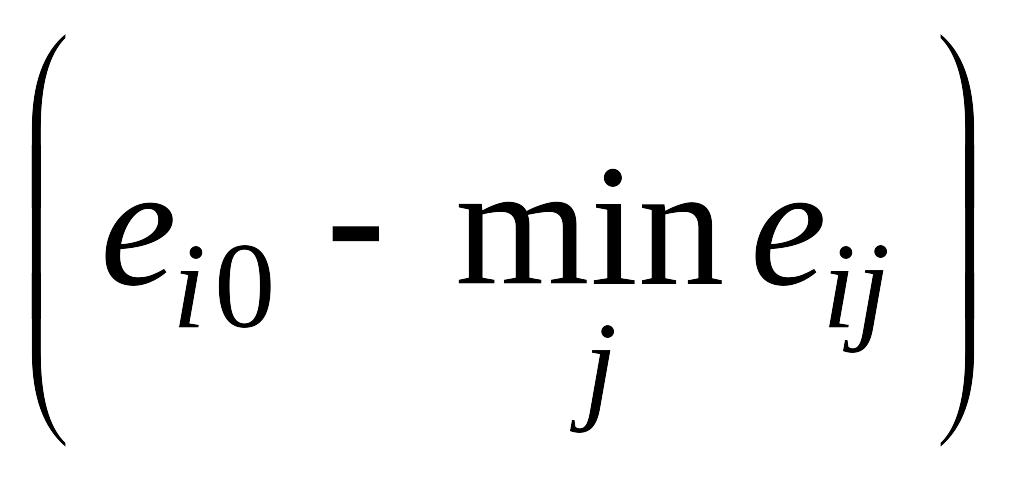 характеризует наибольшие возможные потери в сравнении с опорным решением.

С другой стороны открывается возможность для увеличения выигрыша, по сравнению с ММ, поэтому определяется выигрышное подмножество

.

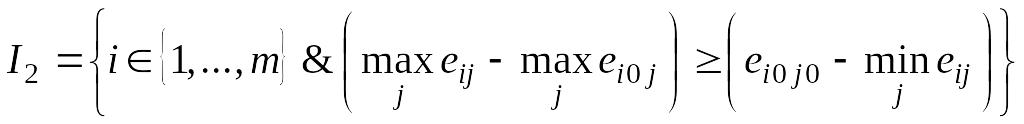После этого определяется .

Оптимальным, в смысле BL(ММ), решением будет следующее:

.

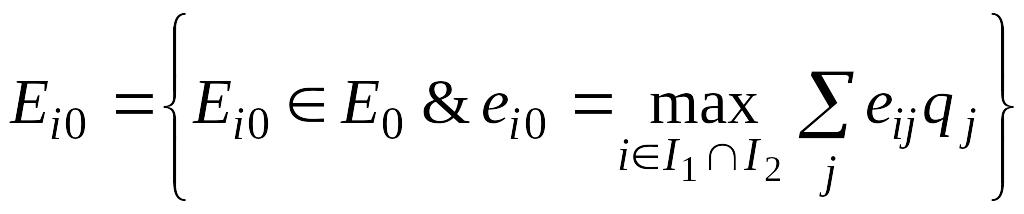Рекомендации по применению:

1. вероятности неизвестны, но есть некоторая априорная информация в пользу некоторого распределения;

2. необходимо считаться с появлением как отдельных, так и их сочетаний;

3. уровень риска определяется величиной ;

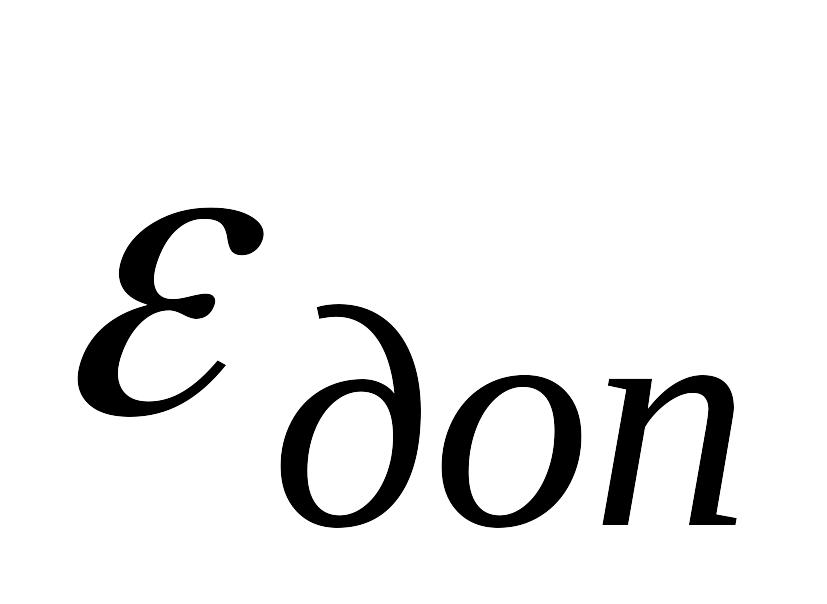4. на число реализаций ограничений нет.

Считается, что BL(ММ) хорошо приспособлен для решения технических задач принятия решений. Однако задание границы риска не учитывает ни число реализаций решения, ни какую либо другую информацию.

Например, условие является существенным только при малом числе реализаций решения.

Домашнее задание. Рассмотреть самостоятельно аналогичную комбинацию критериев BL(S).

5. Критерий произведений (Р)

Применяется для задач фильтрации информации. Применим он только для матриц выигрыша с положительными значениями элементов.

Оценочная функция Р-критерия: , где .

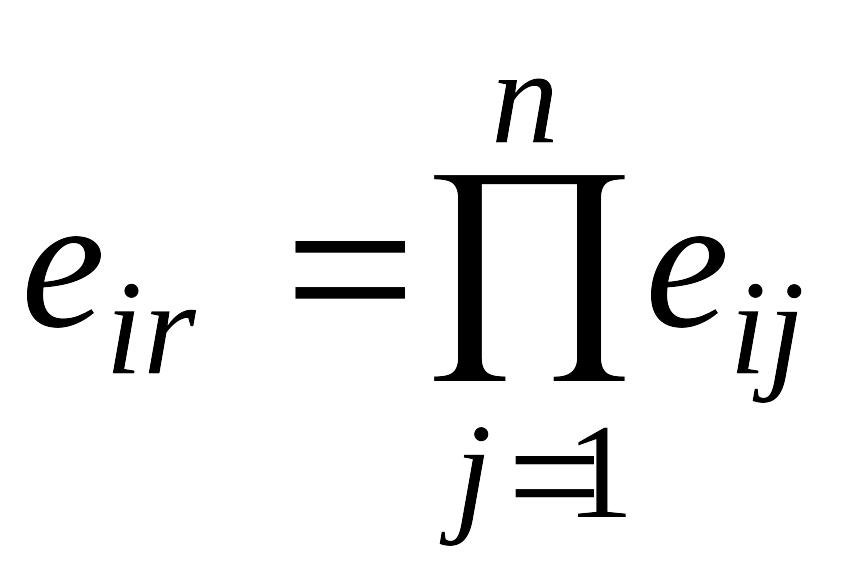Тогда: .

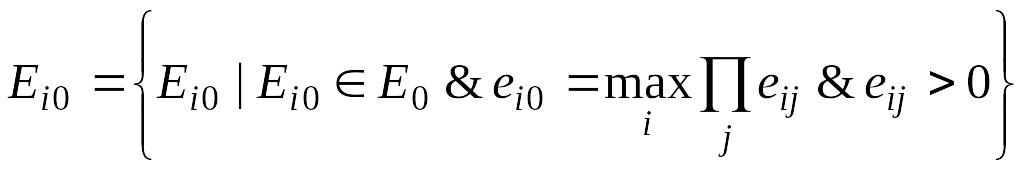Рекомендации по применению:

1. вероятности неизвестны;

2. с появлением отдельных состояний необходимо считаться;

3. критерий применим как для большого, так и для малого числа реализаций;

4. некоторый риск допустим.