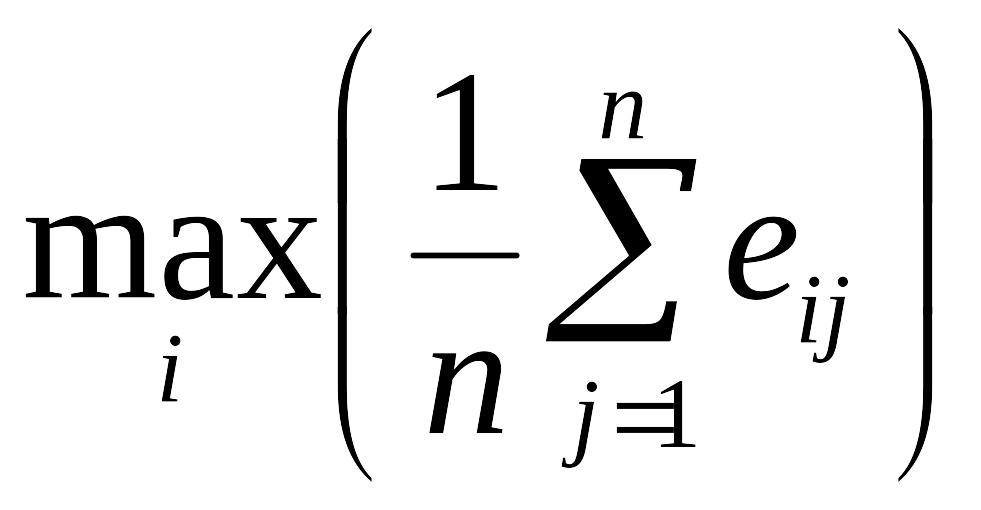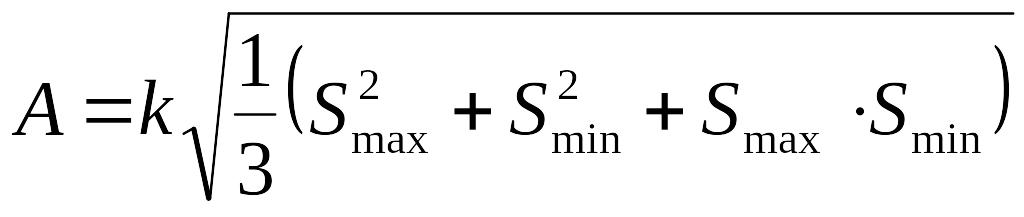Принятие статистических решений

			…		…
…
…

Теория антагонистических игр базируется на предположении о том, что интересы 2-х игроков являются противоположными, и оба действуют активно и разумно. Напротив, в статистических играх участвуют ЛПР и природа, под которой обычно понимают некоторую совокупность внешних не всегда определенных факторов, в условиях которых приходится принимать решение. Природа, по остроумному выражению А.Эйнштейна, ведет себя коварно, но не злонамеренно. Кроме того, у ЛПР имеется возможность путем эксперимента изучать природу. Обозначим через – множество альтернативных решений ЛПР, – множество состояний природы. Тогда статистическая игра описывается матрицей

║ ║, где e_ij - оценка полезности i-го решения в j-й ситуации (выигрыш, надежность и т.п.)

Здесь и далее будем считать, что задана матрица выигрыша (если речь идет о потерях, то платежи отрицательны). Выбор оптимального решения здесь и далее будем производить по следующему критерию:

, (1)

т.е. множество E₀ оптимальных решений состоит из вариантов Е_i0 , которые принадлежат множеству Е, а – максимальная оценка выигрыша при Е_i решении по всем состояниям F_j.

Оценочная функция для статистических игр может быть разной, например:

1. ;

2. – позиция азартного ЛПР;

3. – позиция нейтралитета;

4. – позиция пессимизма;

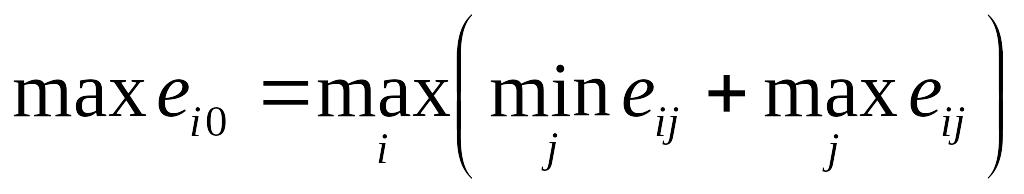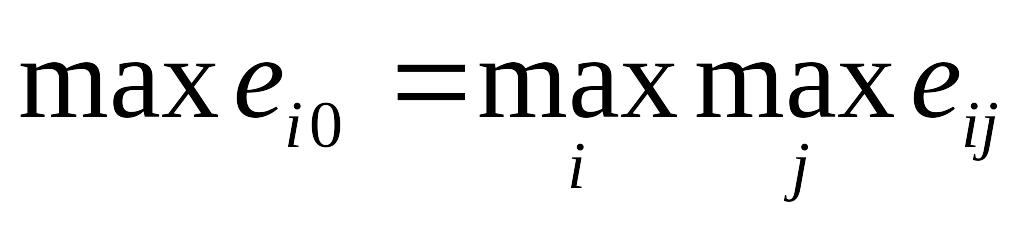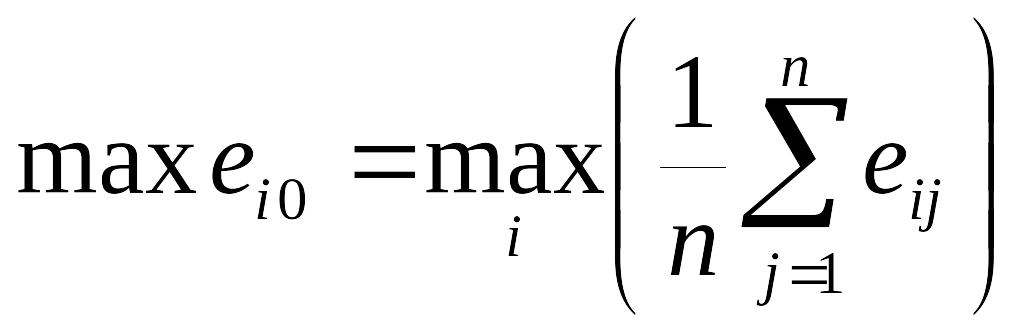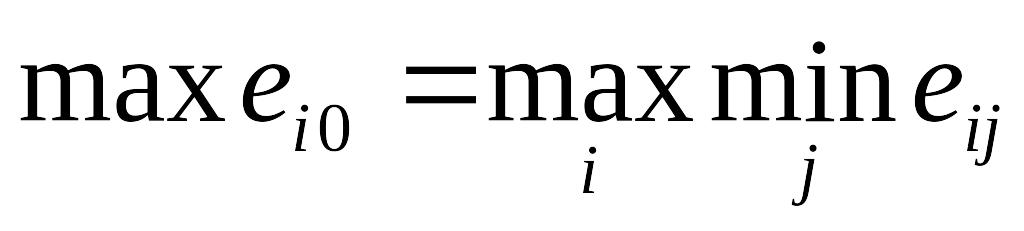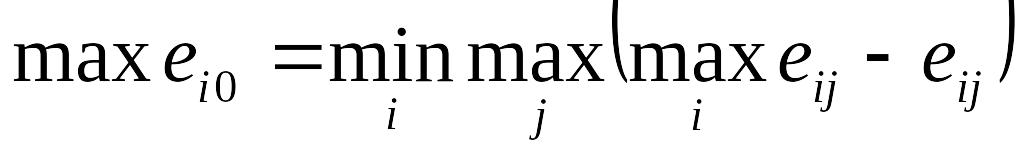5. – позиция относительного пессимизма.

Пример: Необходимо выбрать оптимальное сечение кабеля A при неизвестной токовой нагрузке S, используя приведенные выше оценочные функции. Влияние позиции ЛПР на выбор сечения кабеля при неизвестной токовой нагрузке представлено в таблице:

Позиция ЛПР	Оценочная функция	Результат
Пессимизм
Нейтралитет
Относительный пессимизм
Оптимизм

где k-константа, S_max , S_min – максимальная и минимальная токовая нагрузка. Результаты существенно различаются, при этом выбор окончательного решения определится исключительно позицией ЛПР.

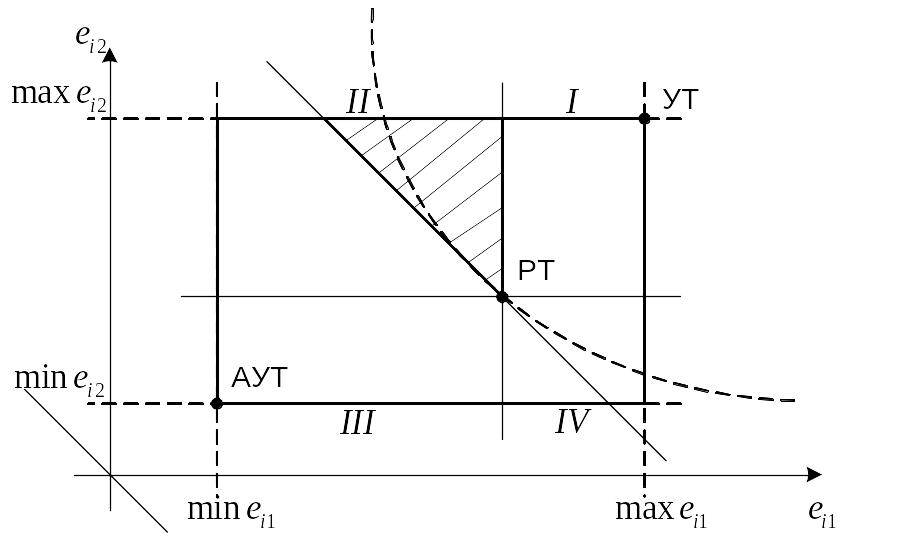
Рассмотрим геометрическую интерпретацию поставленной статистической задачи выбора, что нетрудно сделать для случая двух состояний (n=2). Для этого введем прямоугольную систему координат (ось абсцисс – значение оценочной функции e_i1 , соответствующее состоянию F₁ , а ось ординат – значение e_i2 , соответствующее состоянию F₂). Каждое решение соответствует точке (e_i1 , e_i2) на плоскости:

Найдем на оси абсцисс точку и точку , на оси ординат – точки и . В итоге получится прямоугольник – поле выбора решений или поле полезности. Правый верхний угол прямоугольника назовем утопической точкой (УТ), которая встречается в идеальном случае, когда существует вариант решения, дающий максимальный результат для каждого из двух возможных состояний природы. Аналогичное значение имеет и так называемая антиутопическая точка (АУТ) с координатами ( , ). Все остальные точки лежат внутри прямоугольника или на его границах.

Задача состоит в том, чтобы, используя критерий выбора, найти оптимальное решение. Выберем в поле полезности произвольную точку, которую будем называть рассматриваемой точкой (РТ) и которая лежит внутри прямоугольника. Проведем через нее прямые, параллельные осям координат, которые разделят плоскость на квадранты I, II, III и IV.

Чтобы иметь возможность сравнивать варианты решений с точки зрения их качества, установим на множестве решений Е отношение частичного порядка. Будем говорить, что решение не хуже, чем , если для соответствующих точек и выполняются следующие неравенства: . Причем решение Е_i считается лучше, чем E_j, если хотя бы одно из двух неравенств является строгим.

Рассматривая положение точек поля полезности относительно четырех квадрантов, можно сказать следующее. Все решения, которые представляются точками, лежащими в I квадранте будут лучше, чем РТ, поэтому первый квадрант получил название конуса предпочтения. Соответственно, все точки III квадранта будут хуже РТ и называются антиконусом. Таким образом, оценка качества решений из конуса предпочтения и антиконуса проста и однозначна. Этого нельзя сказать о II и IV квадрантах, их называют областями неопределенности.

Для точек из конусов неопределенности сравнительную оценку можно получить лишь с помощью выбранного критерия К принятия решения, который необходимо либо максимизировать, т.е. найти , либо минимизировать, т.е. найти .

В двумерном случае каждый критерий в общем может быть выражен в виде уравнения кривой , называемую линией уровня или функцией предпочтения для фиксированного значения k.

Пусть, например, функция К имеет вид . Эта функция определяет все прямые на плоскости, параллельные биссектрисе II и IV квадрантов (см. рис. выше). Ранее уже отмечалось, что данный критерий соответствует нейтральной позиции ЛПР (максимизируется среднее значение возможных последствий решений). Поэтому любое решение, расположенное в поле полезности правее и выше проведенной через точку РТ биссектрисы во II и IV квадранте будет более предпочтительным, чем точки, лежащие слева и ниже. Сказанное справедливо и для любого другого критерия с другой функцией предпочтения. Если на основе некоторого критерия получается вогнутая кривая (см. штриховую линию на рис.), то в соответствующей области неопределенности имеется меньшее число лучших точек, чем при нейтральном критерии, т.е. такая кривая характеризует более пессимистическую позицию ЛПР. Наоборот, выпуклая кривая предпочтения будет соответствовать оптимистической позиции ЛПР, т.к. большее число точек из областей неопределенности принадлежит к числу лучших. Предельным случаем пессимистического подхода являются границы I квадранта, а предельным случаем оптимистического подхода - границы III квадранта

Выбор оценочной функции – прерогатива ЛПР, поэтому ПР не является чисто рациональным процессом и требует предварительного выяснения позиции ЛПР. Всякое техническое или экономическое решение в условиях неполной информации принимается в соответствии с какой-либо оценочной функцией с учетом количественных характеристик проблемной ситуации

Особым случаем ПР является фатальная ситуация, когда матрица решений сводится к единственной строке и результат является неизвестным (зависит только от состояния природы):