
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Другий ступінь середнього рівня (бал 5)
1. Зобразити три точки А, В і С, що не лежать на одній прямій. Провести через кожні дві з цих точок пряму. Скільки різних прямих проведено? Позначити їх через точки, які їм належать.
2. Зобразити три точки М, N і K, що не лежать на одній прямій. Скільки різних прямих позначають записи МN, МK і KN? Провести ці прямі.
3. Провести пряму а і зобразити точки А, В і С, що їй належать. Скільки різних прямих позначають записи АВ, BC і АС?
4. Провести пряму АС і позначити точку О, що їй належить. Позначити двома іншими способами пряму АС через точки О, А і С.
5. Позначити три точки А, В і С так, щоб проведених через кожні дві з них прямих було три.
6. Позначити три точки M, N і K і через кожні дві з них провести пряму так, щоб проведено було тільки одну пряму.
Третій ступінь середнього рівня (бал 6)
1. Провести пряму b і позначити три точки так, щоб тільки дві з них належали цій прямій.
2. Зобразити точку K і провести дві прямі m і n так, щоб точка K належала кожній з цих прямих.
3. Зобразити точку В і провести три прямі так, щоб точка В належала тільки двом з цих прямих.
4. Провести пряму m і позначити п’ять точок так, щоб тільки дві з них належали прямій m.
5. Зобразити точку С і провести п’ять прямих так, щоб тільки дві з них проходили через точку С.
6. Зобразити точки А і С і провести три прямі, що перетинаються у точці С і жодна з яких не проходить через точку А.
1. Зобразити прямі a і b, що перетинаються в точці О. Позначити точку М, що належить прямій а, і точку Р, що належить прямій b і точку С, що не належить цим прямим.
2. Зобразити точку О і провести три прямі a, b і c, що проходять через цю точку. Позначити точку М, через яку проходить пряма а, точку N, через яку проходить пряма c, і точку K, через яку не проходить пряма b.
3. Зобразити точку О і провести прямі a і c, що перетинаються в цій точці. Провести пряму d, що не проходить через точку О і перетинає кожну з прямих a і c.
4. Зобразити точку А. Провести прямі а і с, що не проходять через точку А, і пряму m, що проходить через точку А.
5. Зобразити точку М. Провести через неї чотири прямі a, b, c і d та пряму m, що перетинає їх відповідно в точках А, В, С і D. Позначити прямі b і c через точки, що лежать на них.
6. Зобразити точку О. Провести через неї п’ять прямих m, n, k, l і p та пряму a, що перетинає їх відповідно в точках M, N, K, L і P. Позначити прямі n, k і l через дані точки.
Достатній рівень Перший ступінь достатнього рівня (бал 7)
2. Позначити точки А і В, провести через них пряму. Позначити точки K і P, що їй не належать, але лежать на одній прямій з точкою В. 3. Скопіювати рисунок 23 і провести пряму, що проходить через точку М і точку перетину прямих а і b. 4. Скопіювати рисунок 24 і провести через точку М пряму так, щоб всі три прямі мали спільну точку. |
|
|
1. Які з наведених тверджень а)–в) є істинними, а які — хибними? Хибність тверджень проілюструвати рисунком.
а) Будь-які три точки лежать на одній прямій;
б) будь-які дві точки належать одній прямій;
в) через будь-які чотири точки проходить пряма.
2. Доповнити запис до правильного твердження.
Які б не були три точки, вони…
а) належать одній прямій; б) не належать одній прямій;
в) належать або не належать одній прямій.
3. Провести пряму а і позначити три точки, що їй належать, і точку, що їй не належить. Сформулювати твердження про належність будь-яких трьох точок одній прямій.
4. Позначити три точки, через які проходить пряма, і точку, через яку вона не проходить. Сформулювати твердження про кількість прямих, що можна провести через будь-які три точки.
5. Які з наведених тверджень а)–г) є істинними, а які — хибними? Хибність тверджень проілюструвати рисунком.
а) Будь-які чотири точки належать прямій;
б) існує чотири точки, що належать одній прямій;
в) існує чотири точки, що не належать одній прямій;
г) будь-які чотири точки не належать одній прямій.
6. Які з наведених тверджень а)–г) є істинними, а які — хибними?
а) Будь-які сто точок не лежать на одній прямій;
б) серед ста точок будь-які дві лежать на одній прямій;
в) існує сто точок, що лежать на одній прямій;
г) які б не були сто точок, через них можна провести пряму.
1. Якби дві різні прямі мали дві спільні точки, то якій властивості це суперечило б?
2. Якби сто різних прямих проходили через дві дані точки, то якій властивості це суперечило б?
3. Прямі а і с перетинаються в точці О. Відомо, що точка М належить прямій а. Чи може точка М належати прямій с? Відповідь пояснити.
4. Точка М належить двом різним прямим c і d. Відомо, що точка Р належить прямій с. Чи належить точка Р прямій d? Відповідь обґрунтувати.
5. Дві різні прямі a і d проходять через точку О. Точка А належить прямій а. Чи може точка А належати прямій d? Відповідь пояснити.
6. Пряма m проходить через точки А і K та не проходить через точку М. Чи існує пряма, якій належать точки А, K і M? Відповідь пояснити.
Завдання-орієнтир
Пояснити, чому дві прямі не можуть перетинатися у двох точках. Доповнити запис розв’язання.

 Рис. 23
Рис. 23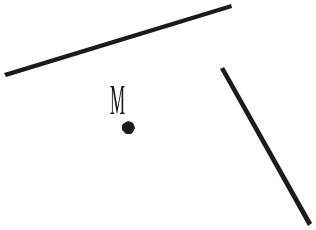 Рис. 24
Рис. 24