
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Третій ступінь достатнього рівня (бал 9)
Спираючись на властивість суміжних кутів, довести, що:
1) якщо два кути рівні, то рівні й суміжні з ними кути;
2) кут, суміжний з гострим кутом, є тупим кутом;
3) кут, суміжний з тупим кутом, є гострим кутом;
4) якщо два суміжні кути рівні, то вони прямі.
1. Дано гострий кут А і тупий кут В, градусні міри яких відносяться як 2 : 3. Знайти градусні міри цих кутів, якщо кут, суміжний з одним з цих кутів, дорівнює 100°.
2. Дано гострий кут А і тупий кут В, градусні міри яких відносяться як 2 : 3. Знайти градусні міри цих кутів, якщо кут, суміжний з одним із цих кутів, дорівнює 110°.
3. Дано гострий і тупий кути, градусні міри яких відносяться як 5 : 24. Знайти градусні міри цих кутів, якщо кут, суміжний з одним із цих кутів, дорівнює 60°.
4. Дано два кути, різниця градусних мір яких дорівнює 110°. Знайти градусні міри цих кутів, якщо кут, суміжний з одним із цих кутів, дорівнює 150°.
Високий рівень Перший ступінь високого рівня (бал 10)
1. Бісектриса кута (ab) утворює з його стороною кут, удвічі більший від кута, суміжного з кутом (ab). Знайти градусну міру кута (ab).
2. Бісектриса кута (cd) утворює з його стороною кут, на 15° більший від кута, суміжного з кутом (cd). Знайти градусну міру кута (cd).
3. Бісектриса кута (ac) утворює з його стороною кут, на 12° менший від кута, суміжного з кутом (aс). Знайти градусну міру кута (aс).
4. Бісектриса кута AOD утворює з його стороною кут, у 4 рази більший від кута, суміжного з кутом AOD. Знайти градусну міру кута AOD.
1. Сума градусних мір кута А і двох суміжних з ним кутів менша від 270°. Довести, що кут, суміжний з кутом А, є гострим.
2. Сума градусних мір кута С і двох суміжних з ним кутів більша від 270°. Довести, що кут, суміжний з кутом С, є тупим.
3. Довести, що коли сума градусних мір кута і двох суміжних з ним кутів менша від 270°, то даний кут є тупим.
4. Довести, що коли сума градусних мір кута і двох суміжних з ним кутів більша від 270°, то даний кут є гострим.
Знайти градусну міру кута, якщо (1–3):
1) третя частина кута дорівнює п’ятнадцятій частині суміжного з ним кута;
2) четверта частина кута дорівнює п’ятій частині суміжного з ним кута;
3) третя частина кута дорівнює суміжного з ним кута.
4. Знайти градусну міру суміжних кутів (ас) і (ас1), якщо 5(ас) = 4(ас1).
1. Градусна міра кута А дорівнює суми градусних мір двох кутів, суміжних з ним. Знайти градусну міру кута А.
2. Один із кутів, утворених при
перетині двох прямих, дорівнює
![]() суми суміжних з ним кутів. Знайти градусну
міру даного кута.
суми суміжних з ним кутів. Знайти градусну
міру даного кута.
3. Градусна міра кута В дорівнює
![]() суми градусних мір двох кутів, суміжних
з ним. Знайти градусну міру кута, суміжного
з кутом В.
суми градусних мір двох кутів, суміжних
з ним. Знайти градусну міру кута, суміжного
з кутом В.
4. Кут (ab), утворений при перетині
двох прямих, дорівнює
![]() суми двох суміжних з ним кутів. Знайти
градусну міру кута, суміжного з кутом
(ab).
суми двох суміжних з ним кутів. Знайти
градусну міру кута, суміжного з кутом
(ab).
Другий ступінь високого рівня (бал 11)
1. Довести, що якщо кут більший від суміжного з ним кута, то він є тупим.
Вказівка. Допустити протилежне, тобто, що кут не є тупим.
2. Довести, що якщо кут менший від суміжного з ним кута, то він є гострим.
3. Довести, що якщо кут, суміжний з даним кутом, більший від нього, то даний кут є гострим.
4. Довести, що якщо кут, суміжний з даним кутом, менший від нього, то даний кут є тупим.
1. Дано кути А і В. Відомо, що сума градусних мір кута А і кута, суміжного з кутом В, дорівнює 140°. Знайти суму градусних мір кута В і кута, суміжного з кутом А.
2. Дано кути С і D. Відомо, що сума градусних мір кута С і кута, суміжного з кутом D, менша від 180°. Довести, що сума градусних мір кута D і кута, суміжного з кутом С, більша від 180°.
3. Дано кути А і С. Відомо, що сума градусних мір кута А і кута, суміжного з кутом С, менша від 180°. Який з кутів більший — А чи С? Відповідь обґрунтувати.
4. Дано кути А і D. Відомо, що сума градусних мір кута А і кута, суміжного з кутом D, дорівнює 200°. Який з кутів — А чи D — більший і на скільки градусів?
5. Дано кути М і О. Відомо, що сума градусних мір кута М і кута, суміжного з кутом О, більша від 180°. Який з кутів — М чи О — більший? Відповідь обґрунтувати.
6. Дано кути О і Р. Відомо, що сума градусних мір кута О і кута, суміжного з кутом Р, дорівнює 160°. Який з кутів — О чи Р — більший і на скільки градусів?
Знайти градусну міру кожного з двох суміжних кутів, якщо:
1) менший з них удвічі більший від їхньої різниці;
2) більший з них удвічі більший від їхньої різниці;
3) один із них дорівнює їхньої різниці;
4) один із них утричі більший від їхньої різниці.
|
|
2. Від променя m у різні півплощини відкладено (mn) = 30° і (mk) = 160° (рис. 384). Знайти градусну міру кута (nk). |
|
3. Від променя а в різні півплощини відкладено (ab) = (ac) = 140°. Знайти градусну міру кута (bc).
4. Від променя OA в різні півплощини відкладено BOA = 95° і СОА = 105°. Знайти градусну міру кута ВОС.

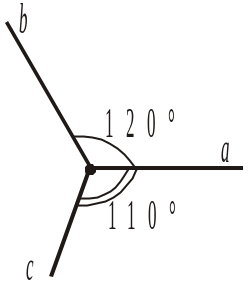 Рис. 383
Рис. 383