
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Достатній рівень Перший ступінь достатнього рівня (бал 7)
Дано: (ab) і (а1b) — суміжні кути. Довести: (ab) + (а1b) = 180°. |
|
1. Кут (аа1) — _____________________________.
2. Градусна міра кута (аа1) дорівнює ___________.
3. Промінь b проходить між сторонами кута ___________.
4. Сума градусних мір суміжних кутів (аb) і (а1b) дорівнює градусній мірі кута ____________, тобто ____________.
Дано: АВС і DBC — суміжні кути. Довести: ABC + DBC = 180°. |
|
1. Кут ABD — _____________________________.
2. Градусна міра кута ABD дорівнює ___________.
3. Промінь BC проходить між сторонами кута ___________.
4. Сума градусних мір суміжних кутів ABC і DBC дорівнює градусній мірі кута ____________, тобто ____________.
|
|
1) (аа1) — розгорнутий, бо промені __________________________.
2) (аа1) дорівнює 180 за ___________________________________.
3) (аа1) = (ас) + (са1), бо промінь с ________________________.
Отже, (ас) + (са1) = 180.
2. За рисунком 378 довести теорему про суміжні кути. |
|
1. Сума двох із чотирьох нерозгорнутих кутів, що утворюються при перетині двох прямих, дорівнює 200°. Чи можуть ці кути бути суміжними? Відповідь пояснити.
2. Чи можуть бути суміжними два гострі кути? Відповідь пояснити.
3. Чи можуть бути суміжними два тупі кути? Відповідь пояснити.
4. Чи можуть бути суміжними прямий і тупий кути? Відповідь пояснити.
5. Чи можуть бути суміжними прямий і гострий кути? Відповідь пояснити.
Завдання-орієнтир
Сума двох із чотирьох нерозгорнутих кутів, що утворилися при перетині двох прямих, дорівнює 100°. Чи можуть ці кути бути суміжними? Відповідь пояснити. Доповнити запис розв’язання задачі.
Розв’язання
Якщо два кути суміжні, то їхня сума дорівнює _______. Так як сума двох даних кутів не дорівнює 180°, то вони ____________________.
Знайти градусну міру кута, якщо він:
1) на 20° більший від суміжного з ним кута;
2) у 4 рази менший від суміжного з ним кута;
3) становить від суміжного з ним кута;
4) становить 25% від суміжного з ним кута.
Другий ступінь достатнього рівня (бал 8)
|
|
2. На рисунку 380 О — точка перетину прямих а і с. 1 + 2 + 3 = 330°. Знайти градусну міру кута 3. 3. Сума градусних мір кута А і двох суміжних з ним кутів дорівнює 220°. Знайти градусну міру одного з кутів, суміжних з кутом А. |
|
4. Сума градусних мір кута D і двох суміжних з ним кутів дорівнює 310°. Знайти градусну міру одного з кутів, суміжних з кутом D.
|
|
2. На рисунку 382 кути АОВ і СОВ — суміжні. OD — бісектриса кута АОВ. DOC = 165°. Знайти градусну міру кутів АОВ і СОВ. |
|
3. (ab) і (а1b) — суміжні кути, с — бісектриса кута (а1b). (са) = 130. Знайти градусну міру кутів (аb) і (а1b).
4. (ac) і (a1c) — суміжні кути. d — бісектриса кута (ас), утворює із променем a1 кут, що дорівнює 135°. Довести, що суміжні кути (ас) і (a1c) рівні.

 Рис. 375
Рис. 375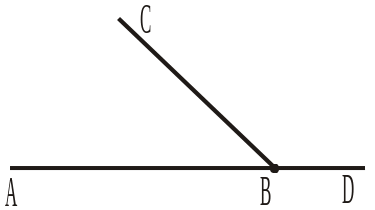 Рис. 376
Рис. 376 Рис. 377
Рис. 377 Рис. 378
Рис. 378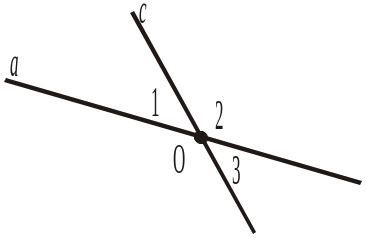 Рис. 379
Рис. 379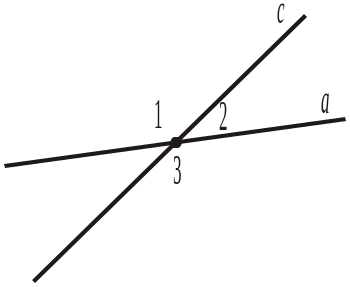 Рис. 380
Рис. 380 Рис. 381
Рис. 381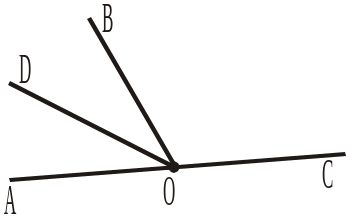 Рис. 382
Рис. 382