
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Середній рівень Перший ступінь середнього рівня (бал 4)
1. Два кути називаються суміжними, якщо в них одна сторона ________________, а дві інші сторони є ________________________. Сума суміжних кутів дорівнює _______________________.
2. Які два кути називаються суміжними і яка їхня властивість?
3. Кути (bd) і (bd1) зі спільною стороною ____ є суміжними, якщо їхні сторони d і d1 є ____________________________________.
4. Кути АОВ і AOD зі спільною стороною ____ є суміжними, якщо їхні сторони ОВ і OD є ____________________________________.
5. Сума кутів (аd) і (аd1), у яких d і d1 — доповняльні промені, дорівнює _____.
6. Сума кутів АOD і AOM, у яких OD і OM — доповняльні промені, дорівнює _____.
|
|
2. На рисунку 369 m і m1 — доповняльні промені. Знайти градусну міру кута (km1), якщо (km) = 152°. |
|
3. На рисунку 370 O — точка прямої АВ. Як називаються кути АОС і ВОС? Знайти градусну міру кута ВОС, якщо АОС = 154°. |
|
4. На рисунку 371 O — точка прямої MN. Як називаються кути MOK і NOK? Знайти градусну міру кута NOK, якщо MOK = 148°. |
|
5. Як називаються кути АОВ і ВОС на рисунку 372? Обчислити градусну міру кута СОВ. 6. Як називаються кути АОD і CОD на рисунку 372? Обчислити градусну міру кута СОD. |
|
Другий ступінь середнього рівня (бал 5)
1. Накреслити за допомогою транспортира АОВ = 45°. Побудувати кут, суміжний з кутом АОВ зі спільною стороною ОА, і обчислити його градусну міру.
2. Накреслити за допомогою транспортира АОС = 130°. Побудувати кут, суміжний з кутом АОС зі спільною стороною ОС, і обчислити його градусну міру.
3. Накреслити за допомогою транспортира (ab) = 20°. Побудувати кут, суміжний з кутом (ab) зі спільною стороною а, і обчислити його градусну міру.
4. Накреслити за допомогою транспортира (mn) = 115°. Побудувати кут, суміжний з кутом (mn) зі спільною стороною n, і обчислити його градусну міру.
1. Накреслити за допомогою транспортира кут А, що дорівнює 40°. Побудувати за допомогою лінійки кут, що дорівнює 140°.
2. Накреслити за допомогою транспортира кут О, що дорівнює 135°. Побудувати за допомогою лінійки кут, що дорівнює 45°.
3. Накреслити за допомогою транспортира кут С, що дорівнює 50°. Побудувати за допомогою лінійки кут, що дорівнює 130°.
4. Накреслити за допомогою транспортира кут D, що дорівнює 170°. Побудувати за допомогою лінійки кут, що дорівнює 10°.
5. Накреслити довільний гострий кут А. Побудувати кут із вершиною у точці А, що в сумі з даним кутом дорівнює 180°.
6. Накреслити довільний тупий кут О. Побудувати кут із вершиною у точці О, що в сумі з даним кутом дорівнює 180°.
Третій ступінь середнього рівня (бал 6)
1. Назвати кути, суміжні з кутом АОС і знайти їхню градусну міру, якщо АОС = 155°. 2. Назвати кути, суміжні з кутом АОD і знайти їхню градусну міру, якщо АОD = 76°. |
|
3. Назвати кути, суміжні з кутом ВОD і знайти їхню градусну міру, якщо ВОD = 152°.
4. Назвати кути, суміжні з кутом ВОС і знайти їхню градусну міру, якщо ВОС = 72°.
На рисунку 374 а і а1 та b і b1 — доповняльні промені. Дати відповіді на питання 5–6. 5. Назвати кути, суміжні з кутом (ab). Знайти їхню градусну міру, якщо (ab) = 98°. 6. Назвати кути, суміжні з кутом (ba1). Знайти їхню градусну міру, якщо (ba1) = 76°. |
|
1. Промінь m, що проходить між сторонами кута (ab), ділить його на кути (am) і (bm), градусні міри яких дорівнюють 15° і 45°. Знайти градусну міру кута (ab1), суміжного з кутом (ab).
2. Промінь, що проходить між сторонами кута, ділить його на кути, що дорівнюють 38° і 62°. Знайти градусну міру кута, суміжного з даним.
3. Бісектриса кута A утворює з його стороною кут, що дорівнює 25°. Знайти градусну міру кута, суміжного з кутом А.
4. Дано суміжні кути (ас) і (а1с). d — бісектриса кута (ас), яка утворює зі стороною а кут (da), що дорівнює 48°. Знайти градусну міру кута (ас1).
5. Бісектриса кута А утворює з його стороною кут 34. Знайти градусну міру кута, суміжного з кутом А.
6. Дано суміжні кути (аm) і (а1m). (am) = 80°. Знайти градусну міру кута (а1d), де d — бісектриса кута (a1m).
Знайти градусну міру кожного з двох суміжних кутів, якщо:
1) один з них утричі більший від іншого;
2) один з них у 9 разів менший від іншого;
3) їхні градусні міри відносяться як 5: 13;
4) один з них у 14 разів більший від іншого;
5) їхні градусні міри відносяться як 1 : 17;
6) їхні градусні міри відносяться як 7 : 2.
Знайти градусну міру кожного з двох суміжних кутів, якщо:
1) один із них на 20° більший від іншого;
2) один із них на 30° менший від іншого;
3) різниця їхніх градусних мір дорівнює 10°;
4) один із них на 100° більший від іншого;
5) один із них на 110° менший від іншого;
6) різниця їхніх градусних мір дорівнює 120°.

 Рис. 368
Рис. 368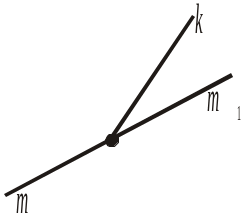 Рис. 369
Рис. 369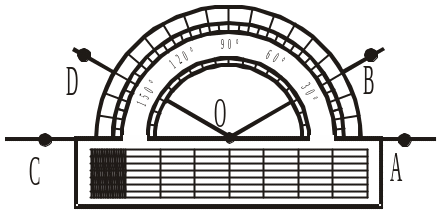 Рис. 372
Рис. 372 Рис. 373
Рис. 373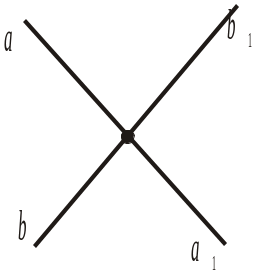 Рис. 374
Рис. 374