
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Другий ступінь початкового рівня (бал 2)
1. На яких з рисунків 353, а)–г) кути 1 і 2 є суміжними?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 353
2. На яких з рисунків 354, а)–г) кути 1 і 2 є суміжними?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 354
3. На яких з рисунків 355, а)–г) кут 1 є суміжним із кутом А трикутника АBC?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 355
4. Які з наведених пар кутів є суміжними?
а) Два кути, що мають спільну точку;
б) два кути, що мають спільну вершину;
в) два кути, у яких дві сторони є доповняльними променями;
г) два кути, у яких одна сторона спільна, а дві інші є доповняльними променями.
5. Які з наведених пар кутів є суміжними?
а) Кути (ad) і (ac), що мають спільну точку;
б) кути (ma) і (na1), у яких сторони а і а1 — доповняльні промені;
в) кути (md) і (md1), у яких сторона m — спільна, а сторони d і d1 — доповняльні промені.
6. Два кути називаються суміжними, якщо в них…
а) спільна вершина;
б) спільна сторона;
в) сторони одного кута є доповняльними променями до сторін другого кута;
г) одна сторона спільна, а дві інші сторони є доповняльними променями.
7. За якої з наведених умов два кути є суміжними?
а) Кути мають спільну сторону;
б) сторона одного кута і сторона другого кута є доповняльними променями;
в) сторони одного кута є доповняльними променями до сторін другого кута;
г) кути мають одну спільну сторону, а дві інші сторони є доповняльними променями.
1. Чи мають два суміжних кути спільну сторону?
а) Не мають; б) мають;
в) не можна визначити: можуть мати, а можуть і не мати.
2. Чи є серед сторін суміжних кутів доповняльні промені?
а) Немає; б) є; в) не можна визначити.
3. Чи є серед сторін суміжних кутів такі, що утворюють розгорнутий кут?
а) Немає; б) є;
в) не можна визначити: можуть бути, а можуть і не бути.
4. b — спільна сторона суміжних кутів (bm) і (bm1). Який кут утворюють прямі m і m1?
5. ОА — спільна сторона суміжних кутів АОВ і АОС. Який кут утворюють промені ОВ і ОС?
а) 90°; б) менше від 180°; в) 180°. |
|
2. На рисунку 357 О — точка прямої АВ. Чому дорівнює сума градусних мір кутів АОС і ВОС? а) 90°; б) 180°; в) даних недостатньо для визначення. |
|
3. Дано два суміжні кути. Чому дорівнює сума їхніх градусних мір? 4. На рисунку 358 О — точка прямої АВ. Чому дорівнює сума градусних мір кутів АОD і ВОD? |
|
Третій ступінь початкового рівня (бал 3)
|
|
1. Як називається кут (аа1)?
2. Чому дорівнює градусна міра кута (аа1)?
3. Як розміщений промінь b відносно сторін розгорнутого кута?
4. Якому куту дорівнює сума суміжних кутів (ab) і (a1b)?
5. Чому дорівнює сума градусних мір суміжних кутів (ab) і (a1b)?
6. Чи зміняться міркування про градусну міру суми суміжних кутів, якщо їх провести за рисунком 360? |
|
7. Вказати на рисунку 360 розгорнутий кут, що є сумою суміжних кутів, і промінь, що проходить між його сторонами.
8. На основі зв’язків з якою геометричною фігурою доводиться твердження (теорема) про суму суміжних кутів?
а) Прямим кутом; б) гострим кутом; в) розгорнутим кутом.
9. Які з наведених властивостей використовуються при доведенні теореми про суміжні кути?
а) Через будь-які дві точки проходить пряма і тільки одна;
б) будь-який кут має градусну міру;
в) розгорнутий кут дорівнює 180°;
г) від будь-якої півпрямої в дану півплощину можна відкласти кут з деякою градусною мірою, меншою від 180°, і тільки один;
ґ) будь-який промінь, який виходить з вершини розгорнутого кута і відмінний від його сторін, проходить між сторонами кута;
д) градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
1. Як знайти градусну міру кута (ab), якщо (a1b) = 75°? |
|
а) 180° + 75°; б) 180° – 75°;
в) 90° – 75°; г) даних недостатньо.
2. Як знайти градусну міру кута (a1b), якщо (ab) = 120°?
а) 180° – 120°; б) 180° + 120°;
в) 120° – 90°; г) даних недостатньо.
3. Один із суміжних кутів дорівнює 108°. Як знайти градусну міру іншого з цих кутів?
а) 180° + 108°; б) 180° – 108°;
в) 90° + 108°; г) даних недостатньо.
4. Якщо один із суміжних кутів дорівнює 70, то другий з цих кутів дорівнює…
а) 90 + 70; б) 180 + 70; в) 180 – 70; г) 90 – 70.
5. Якщо один з суміжних кутів дорівнює n, то другий із цих кутів дорівнює…
а) n; б) 90 + n; в) 90 – n; г) 180 – n.
6. Один із суміжних кутів дорівнює 130. Чому дорівнює другий із цих кутів?
а) 40; б) 50; в) 70; г) 130.
За рисунком 362, а)–в) дати відповіді на запитання 1–6.
|
|
|
а) |
б) |
в) |
Рис. 362
1. Який кут суміжний з гострим кутом?
а) Гострий; б) прямий; в) тупий; г) розгорнутий.
2. Який кут суміжний з тупим кутом?
3. Який кут суміжний із прямим кутом?
4. Який кут не має суміжних кутів?
5. Кути АОВ і АОС — суміжні. Кут АОВ — гострий. Яким є кут АОС?
6. Кути (ab) і (ab1) — суміжні. Кут (ab) — тупий. Яким є кут (ab1)?
На яких з рисунків 363, а)–г)...
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 363
1) зображено один кут, суміжний з кутом (ab);
2) зображено два кути, суміжних з кутом (ab);
3) не зображено кутів, суміжних з кутом (ab)?
4. Дано кут, градусна міра якого 30° (рис. 364). Як за допомогою лінійки (без транспортира) побудувати кут, що дорівнює 150°? |
|
5. Дано кут, градусна міра якого 102° (рис. 365). Як за допомогою лінійки (без транспортира) побудувати кут, що дорівнює 78°? |
|
1) (ab); 2) (a1b); 3) (a1b1); 4) (ab1). |
|
На рисунку 367 О — точка перетину прямих АВ і CD. Назвати кути, суміжні з кутом: 5) АОС; 6) ВОD; 7) COB; 8) AOD. |
|


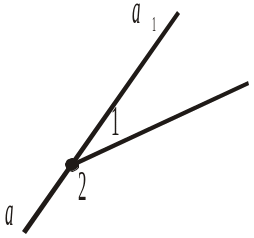
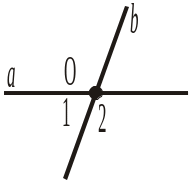
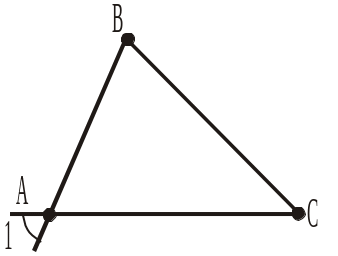
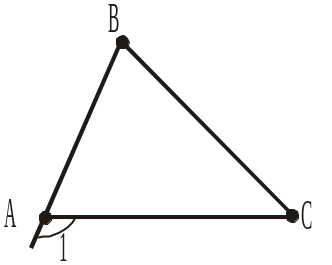

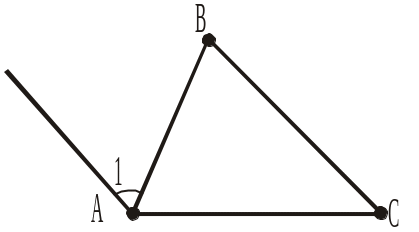
 Рис. 356
Рис. 356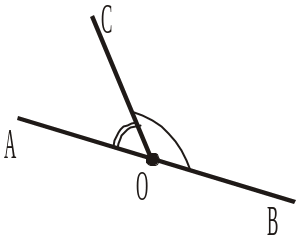 Рис. 357
Рис. 357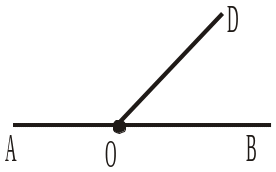 Рис. 358
Рис. 358 Рис. 359
Рис. 359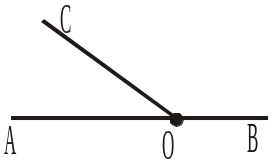 Рис. 360
Рис. 360 Рис. 361
Рис. 361
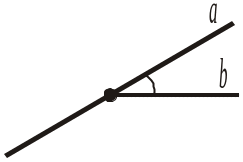
 Рис. 366
Рис. 366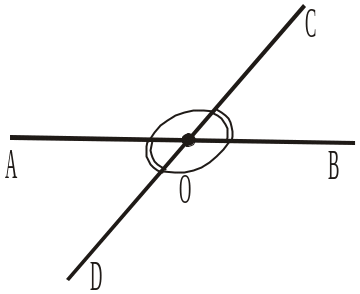 Рис. 367
Рис. 367