
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Високий рівень Перший ступінь високого рівня (бал 10)
1. Довести, що коли пряма перетинає одну з двох паралельних прямих, то вона перетинає і другу з цих прямих.
2. Довести, що коли пряма паралельна до однієї з двох паралельних прямих, то вона паралельна і до другої з цих прямих.
3. Довести, що коли пряма паралельна до однієї з двох прямих, що перетинаються, то другу з цих прямих вона перетинає.
4. Довести, що коли дві прямі паралельні до третьої прямої, то вони паралельні між собою.
Другий ступінь високого рівня (бал 11)
|
|
2. Дано пряму а і дві точки, що лежать у різних півплощинах відносно прямої а. Через кожну з цих точок проведено дві прямі. Скільки найменше і скільки найбільше може бути точок перетину даних прямих із прямою а? Виконати відповідні рисунки.
3. Дано пряму с і три точки, що лежать в одній півплощині відносно цієї прямої. Через кожну з цих трьох точок проведено прямі, паралельні прямій с. Скільки може бути проведено різних прямих? Виконати відповідні рисунки.
4. Дано пряму с і дві точки, що лежать в різних півплощинах відносно цієї прямої. Через кожну з цих точок проведено три прямі. Скільки найменше і найбільше може бути точок перетину даних прямих з прямою а? Виконати відповідні рисунки.
Третій ступінь високого рівня (бал 12)
1. Дано сорок різних прямих, кожні дві з яких паралельні, і пряму с. Відомо, що пряма с перетинає одну із сорока прямих. Довести, що пряма c перетинає і будь-яку іншу з даних сорока прямих.
2. Дано двадцять різних прямих, кожні дві з яких паралельні, і пряму b. Відомо, що пряма b паралельна до однієї з цих двадцяти прямих. Довести, що пряма b паралельна кожній з цих прямих.
3. Дано сто різних прямих, що проходять через точку А, і пряму b, що не проходить через цю точку. Відомо, що пряма b паралельна до однієї з цих ста прямих. Довести, що пряма b перетинає будь-яку іншу з цих ста прямих.
4. Дано десять різних прямих, кожна з яких паралельна прямій с. Довести, що будь-які дві з цих десяти прямих паралельні.
Розділ ІІ. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ
9. СУМІЖНІ КУТИ
Початковий рівень
Перший ступінь початкового рівня (бал 1)
|
|
2. О — точка прямої MN (рис. 347). Назвати спільну сторону кутів KOM і KON та їхні сторони, що є доповняльними променями. |
|
3. C — точка прямої AB (рис. 349). Назвати спільну сторону кутів ACB і BCD та їхні сторони, що є доповняльними променями. |
|
4. О — точка прямої CD (рис. 350). Назвати спільну сторону кутів COM і DOM та їхні сторони, що є доповняльними променями. |
|
|
|
2. О — точка прямої АВ (рис. 352). Як називаються кути COА і СОВ, у яких сторона ОС спільна, а промені ОА і ОВ — доповняльні? |
|
3. Як називаються кути, у яких одна сторона спільна, а дві інші сторони — доповняльні промені?
4. Як називаються кути (ас) і (ас1), у яких сторона а — спільна, а сторони с і с1 — доповняльні промені?
У символічних записах 1)–4) суміжних кутів вказати їхню спільну сторону і доповняльні промені:
1) (ad) і (ad1); 2) (cm) і (dm);
3) MOK і POK; 4) DOA і COA.
Схематично (від руки) зобразити:
1) два суміжні кути з вершиною О;
2) два суміжні кути зі спільною стороною с;
3) два суміжні кути зі спільною стороною ОА;
4) два суміжні кути зі спільною стороною m і доповняльними променями а і а1.

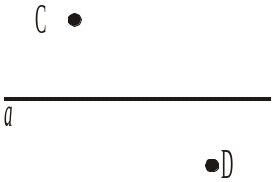 Рис. 346
Рис. 346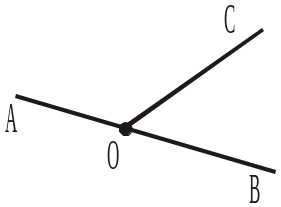 Рис. 347
Рис. 347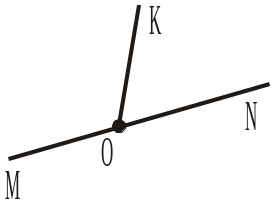 Рис. 348
Рис. 348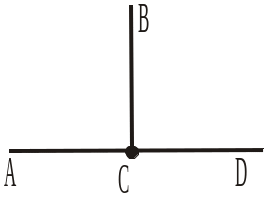 Рис. 349
Рис. 349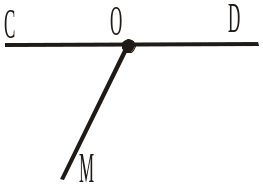 Рис. 350
Рис. 350 Рис. 351
Рис. 351 Рис. 352
Рис. 352