
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Другий ступінь достатнього рівня (бал 8)
|
|
2. Дано пряму а і точку М, що їй не належить (рис. 418). Через точку М проведено три різні прямі. Виконати два рисунки, що ілюструють два можливі випадки розміщення проведених прямих відносно прямої а. Відповідь пояснити.
3. Дано пряму с і точку О, що їй не належить. Через точку О проведено п’ять різних прямих. Як можуть бути розміщені проведені прямі відносно прямої с? Відповідь проілюструвати рисунком і обґрунтувати.
4. Дано пряму d і точку P, що їй не належить. Через точку Р проведено сто різних прямих. Як можуть бути розміщені проведені прямі відносно прямої d? Відповідь обґрунтувати.
1. Дано пряму с і точку М, що їй не належить. Через точку М проведено прямі, що перетинають пряму с у десяти точках. Скільки прямих проведено? Пояснити, чому задача має два розв’язки.
2. Дано пряму і точку, що їй не належить. Через точку проведено декілька прямих. Скільки може бути проведено прямих, якщо точок перетину сто? Відповідь пояснити.
3. Через вершину А трикутника АВС проведено декілька прямих, які перетинають пряму ВС в дев’яти точках. Жодна із прямих не проходить через точки В і С. Скільки прямих проведено? Відповідь пояснити.
4. Через вершину М трикутника MOK проведено декілька прямих, жодна з яких не співпадає із прямими МО і MK. Проведені прямі перетинають пряму OK у двадцяти точках. Скільки прямих проведено? Відповідь пояснити.
Третій ступінь достатнього рівня (бал 9)
|
|
2. Дано паралельні прямі m і n (рис. 338). Пояснити, чому пряма k, що перетинає пряму n у точці K, буде перетинати і пряму m. |
|
3. Через точку М, що лежить поза трикутником АВС (рис. 339), проведено пряму b, яка паралельна прямій АС. Пояснити, чому прямі b і АВ перетинаються. |
|
4. Через точку А, що лежить поза трикутником MOK, проведено пряму а, яка паралельна прямій ОK (рис. 340). Чи перетинатиме пряма ОМ пряму а? Відповідь пояснити, спираючись на основну властивість паралельних прямих. |
|
|
|
2. Дано аd (рис. 342). Обґрунтувати, що кожна пряма, яка паралельна прямій а, буде паралельна і прямій d. |
|
3. Дано прямі m, a і c (рис. 343). Відомо, що пряма m паралельна прямим а і с. Обґрунтувати, що прямі a і с паралельні. |
|
4. Дано прямі р, k і d (рис. 344) такі, що pk, pd. Обґрунтувати, що kd. |
|
Завдання-орієнтир
Дано прямі a, b і c (рис. 345) такі, що ac, ba. Обґрунтувати, що bc. Розв’язання |
|
Вказівка. Провести міркування способом «від супротивного»: зробити припущення, протилежне висновку, і прийти до протиріччя з основною властивістю паралельних прямих.
1. Припустимо, що прямі b і c не паралельні, тобто мають спільну точку.
2. Тоді через цю спільну точку за умовою проходять дві прямі (b і с), які паралельні прямій a.
3. Це неможливо за основною властивістю паралельності прямих.
Отже, прямі b і с паралельні.

 Рис. 336
Рис. 336 Рис. 337
Рис. 337 Рис. 338
Рис. 338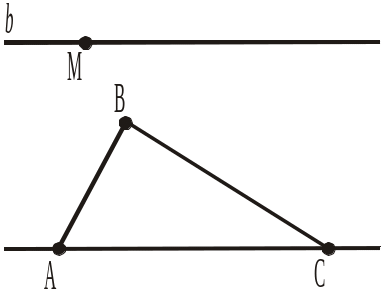 Рис. 339
Рис. 339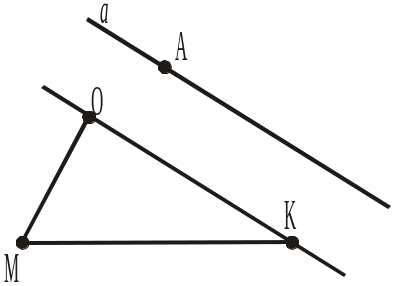 Рис. 340
Рис. 340 Рис. 341
Рис. 341 Рис. 344
Рис. 344