- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Третій ступінь початкового рівня (бал 3)
а) Перетинає пряму b; б) не перетинає пряму b; |
|
в) не можна визначити: може перетинати пряму b, а може і не перетинати.
2. Дано пряму а і точку А, що їй не належить (рис. 306). Через точку А проведено прямі b і c. Відомо, що bа. Якими є прямі а і с? а) Паралельними прямими; б) прямими, що перетинаються; в) не можна визначити: або паралельні, або перетинаються. |
|
3. Дано пряму b і точку С, що їй не належить. Через точку С проведено прямі m і k. Відомо, що прямі b і m паралельні. Якими є прямі b і k?
а) Паралельними прямими;
б) прямими, що перетинаються;
в) не можна визначити: або паралельні, або перетинаються.
4. Дано пряму с і точку D, що їй не належить. Через точку D проведено дві прямі. Відомо, що одна з них перетинає пряму с (рис. 307). Як розміщена друга пряма? а) Паралельна прямій с; б) перетинає пряму с; |
|
в) не можна визначити: або паралельна, або перетинає пряму с.
5. Дано пряму a і точку D, що їй не належить (рис. 308). Через точку D проведено десять різних прямих. Відомо, що одна з них паралельна прямій а. Як розміщені інші дев’ять прямих? а) Усі дев’ять паралельні прямій а; |
|
б) усі дев’ять перетинають пряму а;
в) частина перетинає, а частина не перетинає пряму a.
6. Дано пряму і точку А, що їй не належить. Через точку А проведено пряму, паралельну даній прямій. Якими будуть дана пряма і будь-яка інша пряма, що проходить через точку А?
а) Паралельними прямими; б) прямими, що перетинаються.
Середній рівень Перший ступінь середнього рівня (бал 4)
1. Доповнити запис означення паралельних прямих.
Паралельними прямими на площині називаються дві прямі, що ___________________.
2. Доповнити запис основної властивості паралельних прямих за аксіомою.
Через точку, що не лежить на даній прямій, можна провести на площині _________________________, паралельну даній.
3. Прямі а і m паралельні. Яка їхня властивість за означенням паралельних прямих?
4. Через точку, що не лежить на даній прямій, проведено дві прямі, одна з яких паралельна даній прямій. Якими є друга пряма і дана пряма за основною властивістю паралельних прямих?
5. Через точку, що не лежить на даній прямій, проведено декілька прямих. Скільки серед них прямих, паралельних даній за основною властивістю паралельності?
6. Доповнити запис.
Якщо через точку, що не лежить на даній прямій, проведено декілька прямих, то серед них за основною властивістю паралельності не більше як одна пряма ____________________________________.
Побудувати за допомогою кутника пряму, паралельну прямій, зображеній на рисунках 309–312.
-
1.

2.

Рис. 309
Рис. 310
3.

4.

Рис. 311
Рис. 312
Завдання-орієнтир
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 313
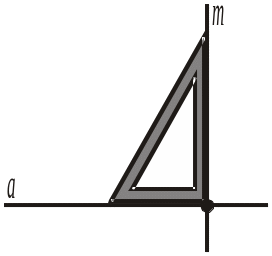
Побудувати за допомогою кутника довільну пряму, паралельну даній прямій а (рис. 313, а), за планом:
1) провести за допомогою кутника пряму m, що перетинає пряму а під прямим кутом (рис. 313, б);
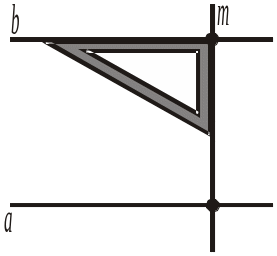
2) через яку-небудь точку прямої m провести пряму b, що перетинає її під прямим кутом (рис. 313, в);
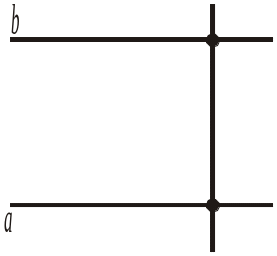
3) прямі b і а паралельні (рис. 313, г).
Скопіювати розміщення прямої і точки, побудувати пряму, що проходить через дану точку і паралельна даній прямій (рис. 314–317):
-
1.

2.

Рис. 314
Рис. 315
3.

4.
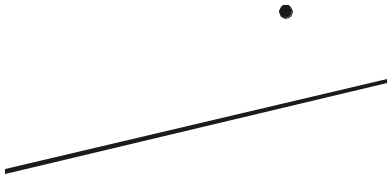
Рис. 316
Рис. 317
Завдання-орієнтир
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 318
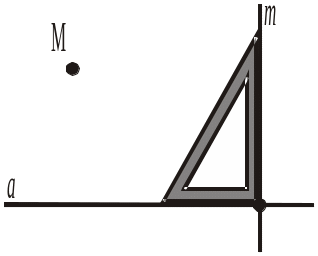
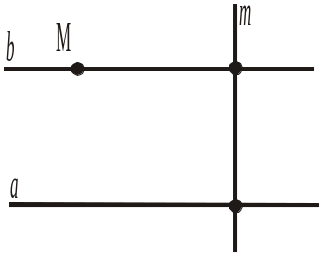
Дано пряму а і точку М, що їй не належить (рис. 318, а). Провести за допомогою кутника через точку М пряму, паралельну прямій а, за планом:
1) провести за допомогою кутника довільну пряму m, що перетинає пряму а під прямим кутом (рис. 318, б);
2) провести через точку М пряму b, що перетинає пряму m під прямим кутом (рис. 318, в);
3) прямі а і b паралельні (рис. 318, г).

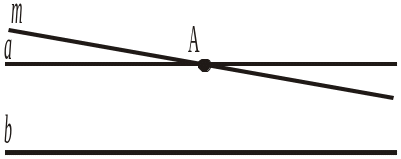 Рис. 305
Рис. 305 Рис. 306
Рис. 306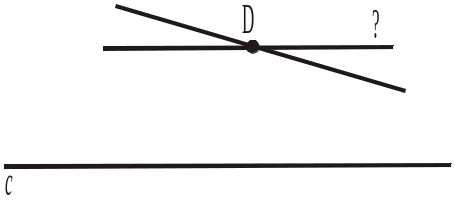 Рис. 307
Рис. 307 Рис. 308
Рис. 308