
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Третій ступінь середнього рівня (бал 6)
1. Побудувати трикутник АВС, у якого А = 50°, АВ = 5 см, В = 70° за планом:
а) провести промінь АМ і відкласти на ньому відрізок AВ = 5 см (рис. 294);
б) відкласти від променя АВ у верхню півплощину KAB = 50° (рис. 295);
в) відкласти від променя ВМ у верхню півплощину PBM = 180° – – 70° = 110° (рис. 296);
г) точку перетину променів AK і PB позначити через С.
АВС — шуканий.
|
|
|
Рис. 294 |
Рис. 295 |
Рис. 296 |
2. Побудувати ABC, у якого АВ = 4 см, А = 60°, В = 80°.
3. Побудувати ABC, у якого АВ = 5 см, А = 75°, В = 30°.
4. Побудувати MOK, у якого MO = 4,5 см, M = 40°, O = 30°.
5. Побудувати ACD, у якого АC = 3,5 см, А = 65°, C = 40°.
6. Побудувати ABD, у якого АВ = 4 см, А = 50°, В = 50°.
Високий рівень Перший ступінь високого рівня (бал 10)
Позначити шістьма різними способами трикутник із вершинами в точках:
1) А, В і С; 2) А, С і D;
3) М, О і K; 4) Р, R і S.
1. На площині позначено точки А, В і D такі, що для трикутника з вершинами у цих точках виконується рівність ABD = ADB. Довести, що у трикутнику з вершинами в даних точках дві сторони рівні.
2. На площині позначено точки М, N і K такі, що для трикутника з вершинами у цих точках виконується рівність MNK = NMK. Довести, що у трикутнику з вершинами в даних точках два кути рівні.
3. На площині позначено точки А, С і D такі, що для трикутника з вершинами у цих точках виконується рівність АСD = CDA. Довести, що у трикутнику з вершинами в даних точках усі кути рівні.
4. На площині позначено точки О, Р і K такі, що для трикутника з вершинами у цих точках виконується рівність OPK = PKO. Довести, що у трикутнику з вершинами в даних точках усі сторони рівні.
Другий ступінь високого рівня (бал 11)
1. Для трикутника з вершинами в точках А, В і С виконується рівність АВС = АCВ. Обчислити периметр цього трикутника, якщо АВ = 5 см, ВС = 6 см.
2. Знайти периметр трикутника з вершинами в точках P, О і K, якщо OP = 7 см, PK = 6 см і для трикутника виконується рівність POK = KOP.
3. Для трикутника з вершинами в точках А, С і D виконується рівність АСD = DАC. Чи можна визначити периметр даного трикутника, якщо відома довжина однієї сторони АС? Якщо можна, то знайти його за умови, що АС = а.
4. Знайти периметр трикутника з вершинами в точках М, О і K, якщо MK = 3 см і для трикутника виконується рівність MOK = KMO.
Третій ступінь високого рівня (бал 12)
1. Зобразити точки А, В і С так, щоб АВ = 5 см і АВС = ВСА.
2. Побудувати трикутник з вершинами в точках М, О і K такий, що МО = 4 см, а для вершин виконується рівність MOK = KMO.
3. Побудувати трикутник з вершинами в точках А, В і С такий, що АВ = 4 см, ВС = 3 см і для вершин виконується рівність АВС = АСВ.
4. Побудувати трикутник з вершинами в точках М, О і K такий, що МО = 4 см, ОK = 5 см і для трикутника виконується рівність MOK = MKO.
|
|
2. Дано шість точок А1, А2, А3, А4, А5 і А6, що лежать на прямій а, і точку О, що не лежить на цій прямій (рис. 298). Кожні дві з семи точок сполучено відрізком. Скільки утворилося трикутників з вершинами в даних точках, однією з яких є точка А3? Скільки всього утворилося трикутників? |
|
3. Дано вісім точок А1, А2, А3, А4, А5, А6, А7 і А8, що лежать на прямій а, і точку О, що не лежить на цій прямій (рис. 299). Кожні дві з дев’яти точок сполучено відрізком. Скільки всього утворилося трикутників, вершинами яких є три з даних точок? |
|
4. Дано сім точок, що лежать на прямій, і точку, що на ній не лежить. Кожні дві точки сполучено відрізком. Скільки всього утворилося трикутників, вершинами яких є три з даних восьми точок?

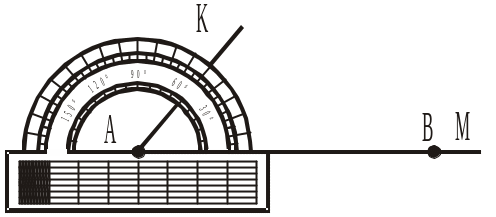
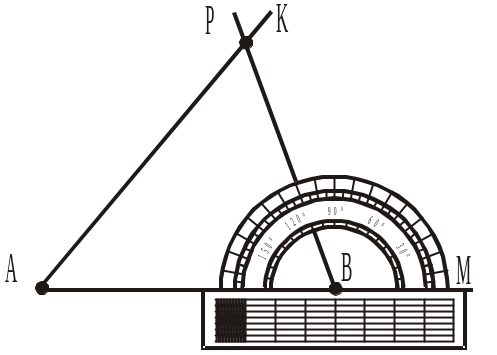
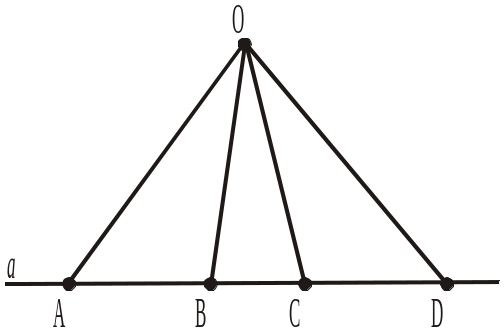 Рис. 297
Рис. 297 Рис. 298
Рис. 298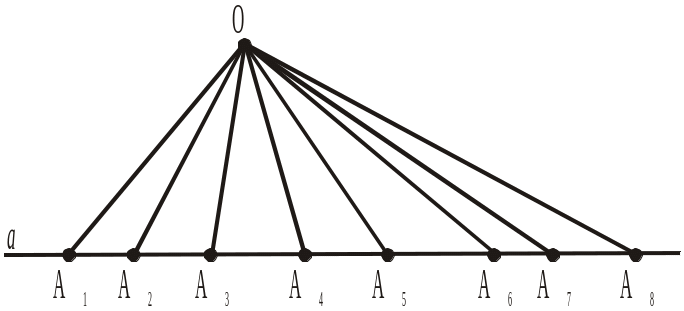 Рис. 299
Рис. 299