
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Другий ступінь початкового рівня (бал 2)
1) усі точки, що належать прямій а; 2) усі точки, що належать прямій b; 3) точки, що належать прямій a і не належать прямій b; 4) точку, що належить і прямій а, і прямій b; 5) точки, що належать прямій a і не належать прямій b; |
|
6) точки, що не належать прямій a і не належать прямій b;
7) точку перетину прямих.
1) усі точки, що належать прямій с; 2) усі точки, що належать прямій d; 3) точку, що належить і прямій c, і прямій d. |
|
1. Дано пряму а. Як розміщені відносно неї точки площини?
а) Усі точки належать прямій а;
б) усі точки не належать прямій а;
в) не можна визначити: є точки, що належать прямій а, і точки, що не належать прямій а.
2. Дано пряму b. Як розміщені відносно неї точки площини?
а) Не можна визначити: є точки, що лежать на прямій b, і точки, що не лежать на прямій b;
б) усі точки лежать на прямій b;
в) усі точки не лежать на прямій b.
3. Дано точку А. Як розміщені відносно неї прямі площини?
а) Усі прямі проходять через точку А;
б) усі прямі не проходять через точку А;
в) не можна визначити: є прямі, які проходять через точку А, і є прямі, які не проходять через точку А.
4. Дано пряму a. Як розміщені точки площини відносно цієї прямої за основною властивістю належності?
а) Усі точки площини належать прямій а;
б) усі точки площини не належать прямій а;
в) точки площини або належать прямій а, або не належать їй.
5. Доповнити запис основної властивості належності точок прямій.
Яка б не була пряма, на площині існують…
а) тільки точки, що їй належать;
б) тільки точки, що їй не належать;
в) точки, що належать цій прямій, і точки, що їй не належать.
6. Дано пряму а. Як може бути розміщена відносно неї деяка точка С?
7. Дано точку А. Як може бути розміщена відносно неї деяка пряма a?
1. Дано точку. Чи можна через неї провести пряму?
а) Так; б) ні;
в) існують точки, через які можна провести пряму, та існують точки, через які не можна провести пряму.
2. Дано точку А. Скільки прямих можна провести через неї?
а) Одну; б) дві; в) жодної; г) безліч.
3. На площині задано точку. Скільки прямих можна провести через неї?
1. Дано дві точки. Чи можна провести через них пряму?
а) Так; б) ні;
в) не можна визначити: існують такі дві точки, через які можна провести пряму, та існують такі дві точки, через які не можна провести пряму.
2. Дано дві точки. Чи існує пряма, якій належать обидві точки?
а) Так; б) ні; в) не можна визначити.
3. Дано дві точки. Скільки можна провести через них прямих?
а) Більше, ніж одну; б) одну або жодної; в) одну і тільки одну; в) дві.
4. Дано дві точки. Скільком прямим можуть належати обидві точки одночасно?
а) Безлічі; б) одній або жодній; в) одній і тільки одній; г) двом.
5. Скільки прямих можна провести через будь-які дві точки?
а) Одну або жодної; б) одну і тільки одну; в) більше, ніж одну.
6. Чи існують на площині дві точки, через які не можна провести пряму?
7. Чи існують на площині дві точки, через які можна провести більше, ніж одну пряму?
8. Скільком прямим належать точки М і K, зображені на рисунку 15? а) Одній і тільки одній; б) жодній; в) більше, ніж одній. |
|
9. Доповнити запис основної властивості належності точок і прямих.
Через будь-які дві точки…
а) можна провести більше, ніж одну пряму;
б) проходить або не проходить пряма;
в) можна провести одну і тільки одну пряму;
г) можна провести хоча б одну пряму.
1. На якому з рисунків 16, а)–г) точка А є точкою перетину прямих m і n?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 16
2. Яку точку називають точкою перетину двох прямих?
а) Точку, що належить одній із прямих;
б) точку, що належить кожній із двох прямих;
в) точку, що належить хоча б одній прямій.
3. Яка з наведених точок є точкою перетину прямих a і m?
а) Точка А, що лежить на прямій a і не лежить на прямій m;
б) точка М, що лежить на прямій m і не лежить на прямій a;
в) точка О, що лежить на прямій a і на прямій m;
г) точка D, що не лежить на прямій a і не лежить на прямій m.
4. Точка С називається точкою перетину прямих а і b, якщо вона…
а) лежить хоча б на одній з прямих a і b;
б) належить і прямій a, і прямій b;
в) належить прямій a;
г) належить прямій b.
1. Як називаються прямі, що мають спільну точку?
а) Паралельні прямі; б) прямі, що перетинаються.
2. Скільки спільних точок мають дві різні прямі, що перетинаються?
а) Одну і тільки одну; б) дві; в) більше, ніж одну.
3. У скількох точках можуть перетинатися дві прямі?
а) У двох; б) у декількох; в) в одній і тільки одній.
4. О — спільна точка прямих a і c. Чи можуть прямі a і c мати ще одну спільну точку?
а) Так; б) ні;
в) не можна визначити: можуть мати, а можуть і не мати.
5. Прямі АВ і CD перетинаються в точці О (рис. 17). Чи існує інша точка, у якій перетинаються прямі АВ і CD? а) Так; б) ні; в) не можна визначити. 6. Прямі MN і PK перетинаються в точці С. Чи існує інша точка, що належить прямій MN і прямі PK? |
|
7. Прямі b і с перетинаються в точці D. Скільки всього точок перетину вони мають?

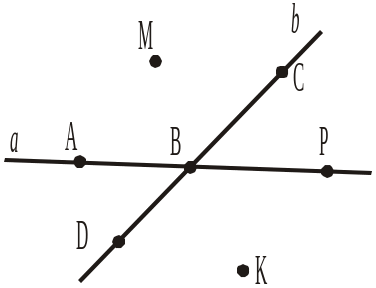 Рис. 13
Рис. 13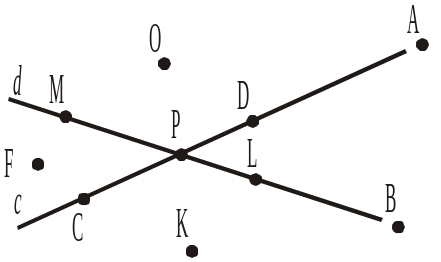 Рис. 14
Рис. 14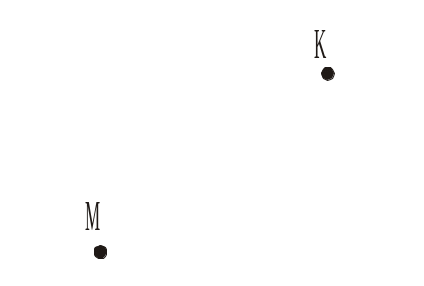 Рис. 15
Рис. 15
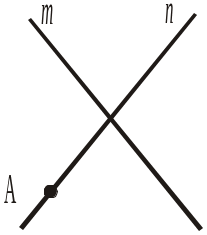
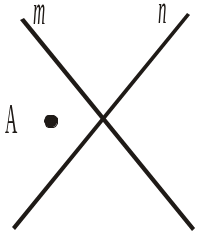

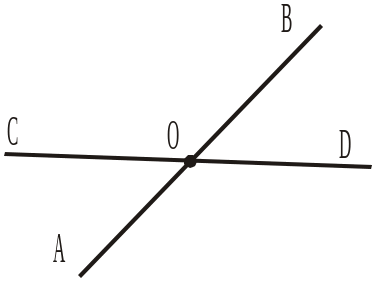 Рис. 17
Рис. 17