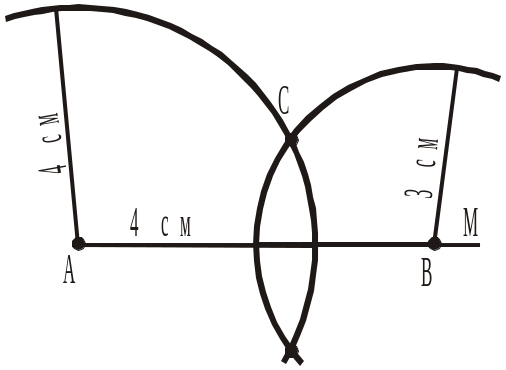- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Середній рівень Перший ступінь середнього рівня (бал 4)
Доповнити запис означення (1–2).
1. Трикутником називається ____________________, що складається із трьох ___________, які _______________, і трьох _______________, що попарно _____________________________.
2. Два трикутники називаються рівними, якщо три кути і протилежні їм _____________ одного трикутника відповідно дорівнюють _________ кутам і ______________________ другого трикутника.
3. Доповнити записи рівності сторін.
Дано: АВС = MOK.
АВ = __________ АС = __________ ВС = __________
4. Доповнити записи рівності кутів.
Дано: АСD = OPK.
О = __________ С = __________ K = __________
5. Доповнити записи рівності сторін.
Дано: АСD = POK.
PO = __________ OK = __________ PK = __________
6. Доповнити записи рівності кутів.
Дано: АMK = CBD.
C = __________ D = __________ B = __________
1. Дано АВО = МKN. Записати рівні сторони і рівні кути трикутників.
2. Дано АBC = МОK. АВ = 4 см, АС = 7 см і BC = 5 см. Знайти довжини сторін трикутника МОK.
3. Дано АСD = МОK. М = 20, K = 70 і О = 90. Знайти градусну міру кутів трикутника АСD.
4. АВС = PMK. Відомо, що В = 30°, Р = 100° і K = 50°. Знайти градусну міру кутів А, С і М.
5. АОС = BOD. ВО = 5 см, BD = 7 см, OD = 8 см. Знайти сторони трикутника АОС.
6. АОС = MPK. А = 50°, О = 70°, С = 60°. Знайти градусну міру найбільшого кута трикутника MPK.
1. Дано АBC = NОK. Знайти периметр трикутника NОK, якщо відомо, що АВ = 6 см, BC = 9 см і NK = 13 см.
2. Дано MOK = ACD. Знайти периметр трикутника ACD, якщо відомо, що МО = 6 см, MK = 7 см і CD = 11 см.
3. Дано ABD = MNK. Знайти периметр трикутника MNK, якщо відомо, що AB = 5 см, AD = 13 см і NK = 9 см.
4. Дано ACD = POK. Знайти периметр трикутника ACD, якщо відомо, що PO = 3,4 см, OK = 5,6 см і AD = 7 см.
На рисунках 280–282 зображено рівні трикутники і позначено однаково їхні рівні кути. Записати рівні сторони трикутників та рівність трикутників (1–3).
1.
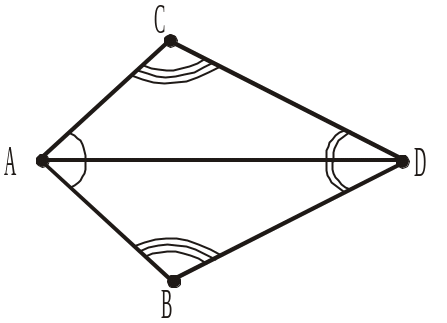
2.
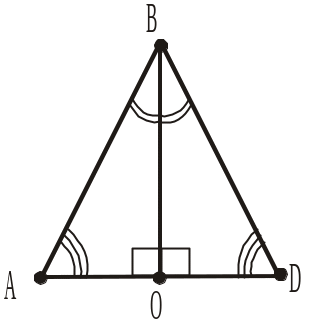
3.
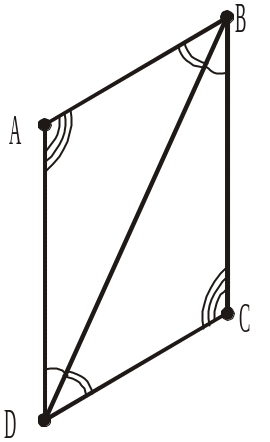
Рис. 280
Рис. 281
Рис. 282
На рисунках 283–285 зображено рівні трикутники і однаково позначено їхні рівні сторони. Записати рівні кути трикутників та рівність трикутників (1–3).
-
1.
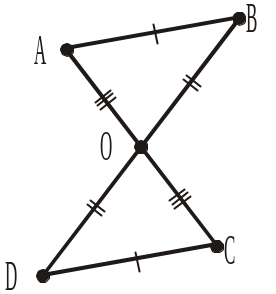
2.
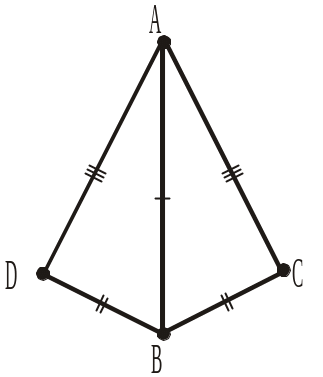
3.
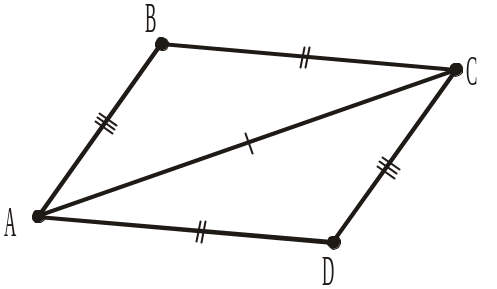
Рис. 283
Рис. 284
Рис. 285
Другий ступінь середнього рівня (бал 5)
1. Побудувати трикутник АВС, у якого А = 60°, АВ = 6 см і АС = 4 см за планом:
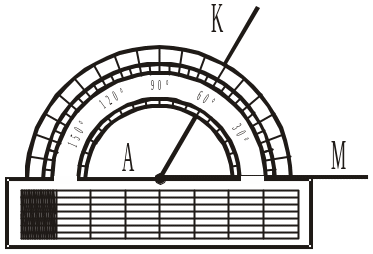
а) провести промінь АМ і побудувати KAM = 60° (рис. 286);
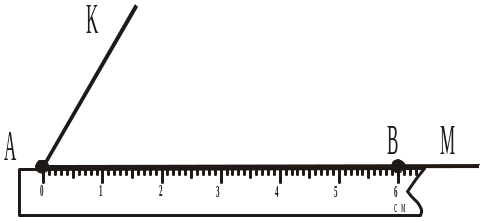
б) на промені АМ відкласти відрізок АВ = 6 см (рис. 287);
в) на промені AK відкласти відрізок АС = 4 см (рис. 288);
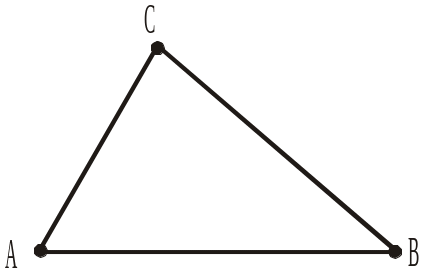
г) сполучити відрізком точки С і В (рис. 289).
|
|
Рис. 286 |
Рис. 287 |
|
|
Рис. 288 |
Рис. 289 |
2. Побудувати ABC, у якого А = 40°, АВ = 3 см, АС = 4,5 см.
3. Побудувати MOK, у якого M = 80°, MO = 2,5 см, MK = 4 см.
4. Побудувати OPK, у якого O = 100°, OP = 3 см, OK = 4 см.
5. Побудувати ACD, у якого А = 110°, АC = 4 см, АD = 2,5 см.
6. Побудувати ABD, у якого А = 80°, АВ = 3,5 см, АD = 5 см.
1. Побудувати трикутник АВС, у якого АВ = 6 см, АС = 4 см і ВС = 3 см за планом:
а) провести промінь АМ і відкласти на ньому AВ = 6 см (рис. 290);
б) описати коло з центром у точці А радіуса 4 см (рис. 291);
в) описати коло з центром у точці В радіуса 3 см; точку перетину кіл позначити через С (рис. 292);
г) сполучити точку С з точками А і В відрізками (рис. 293).
|
|
Рис. 290 |
Рис. 291 |
|
|
Рис. 292 |
Рис. 293 |
2. Побудувати ABC, у якого АВ = 3 см, АС = 4 см, ВС = 5 см.
3. Побудувати MOK, у якого MO = 4,5 см, MK = 3 см, OK = 4 см.
4. Побудувати ACD, у якого АC = 2,4 см, АD = 3,6 см, СD = 5 см.
5. Побудувати ABD, у якого АВ = 1,8 см, АD = 2,8 см, ВD = 3,8 см.
6. Побудувати OPK, у якого OP = 3 см, OK = 3,5 см, PK = 2 см.