
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Другий ступінь початкового рівня (бал 2)
1. На яких з рисунків 269, а)–г) три точки можуть бути вершинами трикутника, а на яких — ні?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 269
2. Дано трикутник АВС. Чи існує пряма, яка містить точки А, В і С?
а) Існує; б) не існує;
в) не можна визначити: або існує, або не існує.
3. Яка з наведених фігур називається трикутником АВС?
а) фігура, що складається з точок А, В і С, і трьох відрізків, що їх попарно сполучають;
б) фігура, що складається з відрізків АВ, АС і ВС;
в) фігура, що складається з точок А, В і С, які не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки.
4. Трикутником називається фігура, яка складається…
а) із трьох відрізків;
б) із трьох точок і трьох відрізків, що сполучають ці точки;
в) із трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки.
5. Що позначає запис «АВС»?
а) три точки А, В і С;
б) три точки А, В і С, що не лежать на одній прямій;
в) три точки А, В і С і три відрізки АВ, АС і ВС, що їх попарно сполучають;
г) три точки А, В і С, що не лежать на одній прямій, і три відрізки АВ, АС і ВС, що їх попарно сполучають.
1. Сторони трикутника дорівнюють 3 см, 4 см і 5 см. Чому дорівнюють сторони рівного йому трикутника?
2. Кути трикутника дорівнюють 30°, 40° і 110°. Яка градусна міра кутів трикутника, що рівний цьому трикутнику?
3. Одна зі сторін трикутника дорівнює 10 см, а кут, що лежить проти неї, дорівнює 30°. Яка градусна міра кута, що лежить проти сторони завдовжки 10 см у трикутнику, рівному даному?
4. Один з кутів трикутника дорівнює 15°, а протилежна йому сторона дорівнює 20 см. Чому дорівнює довжина сторони трикутника, що лежить проти кута 15° у трикутнику, що дорівнює даному?
1. Доповнити записи 1)–6).
Дано: АВС = MOK.
1) АВ = ...
а) ВС; б) АС; в) MO;
г) MK; ґ) OK;
2) АС = ...
а) АВ; б) BC; в) MO;
г) MK; ґ) OK;
3) ВC = ...
а) AВ; б) АС; в) MO;
г) MK; ґ) OK;
4) А = ...
а) В; б) С; в) M;
г) O; ґ) K;
5) B = ...
а) A; б) С; в) M;
г) O; ґ) K;
6) C = ...
а) A; б) B; в) M;
г) O; ґ) K.
2. Доповнити записи 1)–6). ACD = OPR.
1) А = ...; 2) D = ...; 3) P = ...;
4) AD = ...; 5) OP = ...; 6) PR = ... .
3. Доповнити записи 1)–6). ACD = ABM.
1) AC = …; 2) D = …; 3) AB = …;
4) M = …; 5) BM = …; 6) C = … .
1. ACD = PQR. AC = 15 см. Назвати сторону трикутника PQR, що дорівнює 15 см.
а) PQ; б) PR; в) QR.
2. AВС = PQR. R = 28°. Назвати кут трикутника АВС, що дорівнює 28°.
а) А; б) В; в) С.
3. ABD = OMK. D = 52°. Назвати кут трикутника OMK, що дорівнює 52°.
4. ABC = XOZ. OZ = 8 см. Назвати сторону трикутника ABC, що дорівнює 28 см.
Третій ступінь початкового рівня (бал 3)
На рисунку 270 від прямої а відкладено трикутник, що рівний трикутнику АВС, і відмічено дві пари відповідно рівних кутів. Дати відповідь на запитання 1–6.
|
|
Рис. 270
1. Якими є кути С і N?
а) Рівними; б) нерівними;
в) не можна визначити: або рівними, або нерівними.
2. Назвати сторони, що лежать проти кутів А і K.
3. Якими є сторони СВ і NM, що лежать проти відповідно рівних кутів А і K?
4. Назвати сторони, що лежать проти кутів В і М.
5. Якими є сторони АС і KN, що лежать проти відповідно рівних кутів В і М?
6. Якими є сторони АВ і MK, що лежать проти відповідно рівних кутів С і N?
На рисунку 271 від прямої с відкладено трикутник, що рівний трикутнику АВС, і відмічено дві пари відповідно рівних сторін. Дати відповіді на запитання 1–6.
|
|
Рис. 271
1. Якими є сторони АС і МО?
2. Назвати кути, що лежать проти сторін АВ і MP.
3. Якими є кути С і О, що лежать проти рівних сторін АВ і МР?
4. Назвати кути, що лежать проти сторін ВС і ОР.
5. Якими є кути А і М, що лежать проти рівних сторін ВС і ОР?
6. Якими є кути В і Р, що лежать проти рівних сторін АС і ОМ?
1. СВ = ... . 2. С = ... . 3. САВ = ... . 4. СВА = ... . 5. АСВ = ... . 6. АВС = ... . 7. САВ = ... . 8. СВА = ... . |
|
|
|
|
|
1. АСВ = ...
а) MOK; б) MKO; в) OKM;
2. ABC = ...
а) MOK; б) MKO; в) OKM;
3. CAB = ...
а) KOM; б) KMO; в) OKM;
4. CBA = ...
а) KOM; б) KMO; в) OKM;
5. BAC = ...
а) OMK; б) MKO; в) OKM;
6. BCA = ...
а) OMK; б) MKO; в) OKM.
|
|
1. ACD = ...
а) PKO; б) POK; в) KPO;
2. ADC = ...
а) PKO; б) POK; в) KPO;
3. DAC = ...
а) KPO; б) KOP; в) PKO;
4. CDA = ...
а) ОKP; б) KOP; в) PKO.
1. AВD = ... а) CDB; б) CBD; в) DBC; 2. ADВ = ... а) CDB; б) CBD; в) DBC; 3. ВАD = ... а) ВDС; б) BСD; в) DBC; 4. ВDА = ... а) ВDС; б) BСD; в) DСB. |
|
1) вершина А; 2) вершина В; 3) вершина С. |
|
4. Назвати трикутник з вершинами у точках D, О і K двома способами, щоб на першому місці в записі була вершина: D; О; K.
5. А, С і D — вершини трикутника. Скількома різними способами можна позначити трикутник з вершинами в цих точках?
а) Одним; б) двома; в) трьома; г) шістьма.
6. Записати шість можливих способів позначення трикутника з вершинами в точках А, С і О.
На площині позначено три точки А, В і С такі, що для трикутника з вершинами в цих точках виконується рівність: АВС = АСВ. Дати відповіді на питання 1–4.
1. Якими є кути В і С трикутника АВС?
а) Рівними; б) нерівними;
в) не можна визначити: або рівними, або нерівними.
2. Якими є кути А і С трикутника АВС?
а) Рівними; б) нерівними;
в) не можна визначити: або рівними, або нерівними.
3. Якими є кути А і В трикутника АВС?
а) Рівними; б) нерівними;
в) не можна визначити: або рівними, або нерівними.
4. Якими є сторони АВ і АС трикутника АВС?
а) Рівними; б) нерівними;
в) не можна визначити: або рівними, або нерівними.
На площині позначено три точки А, В і С такі, що для трикутника з вершинами у цих точках виконується рівність: АВС = ВСА. Дати відповідь на питання 1–8. Якими у трикутнику з вершинами у точках А,В і С є:
1) кути А і В; 2) кути А і С;
3) кути В і С; 4) усі кути А, В і С;
5) сторони ВС і СА; 6) сторони АВ і ВС;
7) сторони АС і АВ; 8) усі сторони АВ, ВС і АС?
1) три точки, що не є вершинами трикутника; 2) трикутник зі стороною АВ; 3) трикутник зі стороною АС; 4) трикутник зі стороною ВС; 5) трикутник зі стороною AD; |
|
6) трикутник зі стороною BD;
7) трикутник зі стороною DC.
1) А і В; 2) А і С; |
|
3) В і С; 4) А і О;
5) В і О; 6) С і О.
Назвати і вказати кількість трикутників із вершиною:
7) А; 8) В;
9) С; 10) О.
11. Скільки всього трикутників зображено на рисунку 278?
а) Один; б) два; в) три; г) чотири.
12. Яка точка є вершиною кожного із трьох трикутників, зображених на рисунку 278?
а) А; б) В; в) С; г) О.
1) А і В; 2) А і С; 3) А і D; 4) В і D. |
|
Назвати точки, з якими не утворюють трикутник точки:
5) А і В; 6) А і D;
7) В і С; 8) С і D.
9. Назвати точку, яка є вершиною кожного із трикутників, зображених на рисунку 279.
а) А; б) С; в) О; г) В.
Назвати трикутники, вершинами яких є точки:
10) А і О; 11) О і В;
12) О і С; 13) О і D.
14. Скільки всього трикутників зображено на рисунку 279?
а) Три; б) чотири; в) шість; г) вісім.

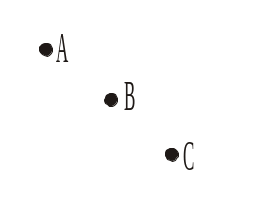
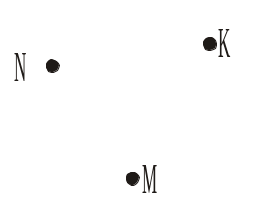

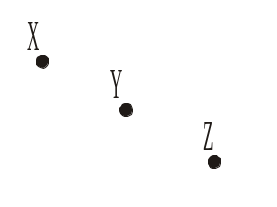

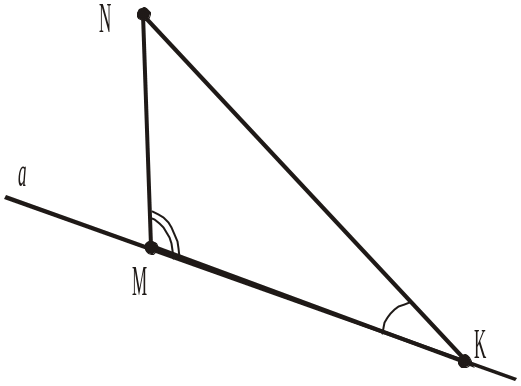
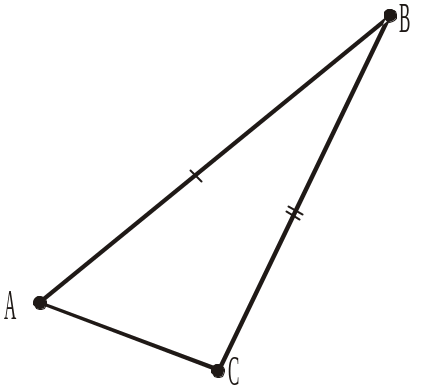
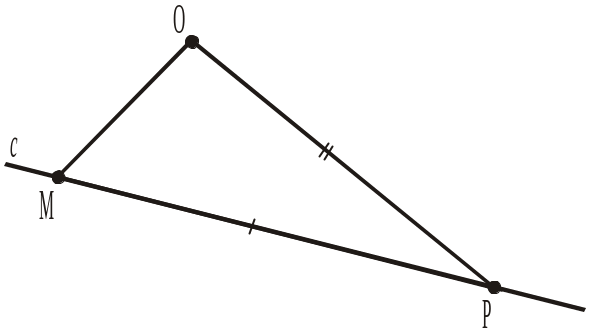
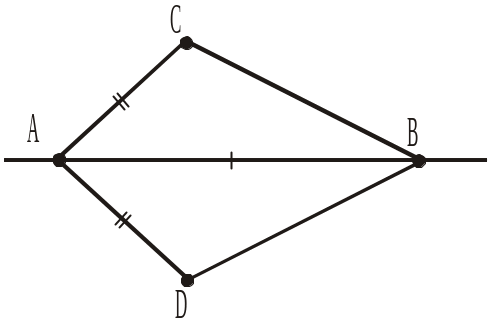 Рис. 272
Рис. 272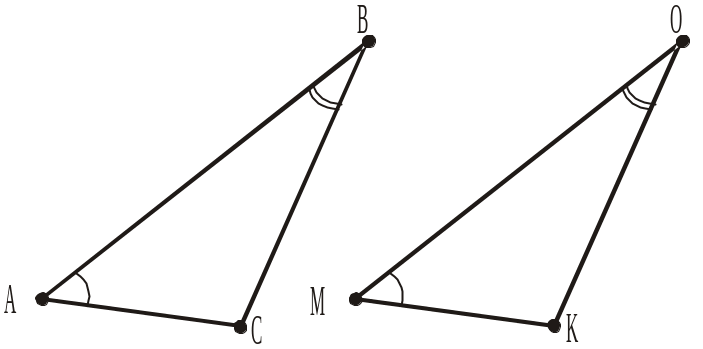 Рис. 273
Рис. 273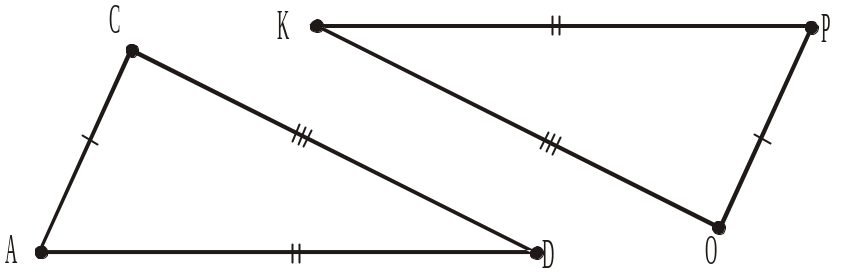 Рис. 274
Рис. 274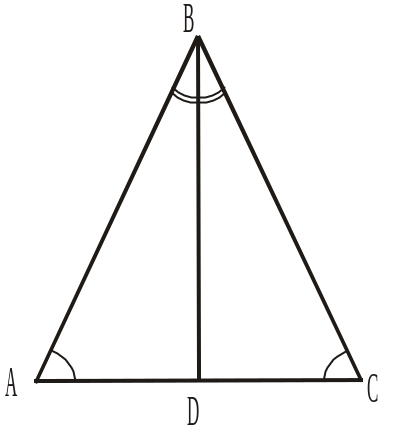 Рис. 275
Рис. 275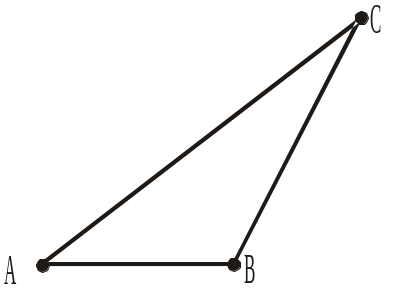 Рис. 276
Рис. 276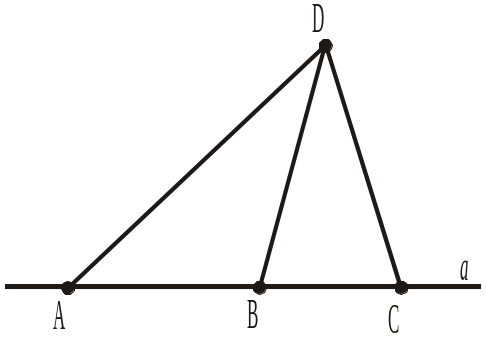 Рис. 277
Рис. 277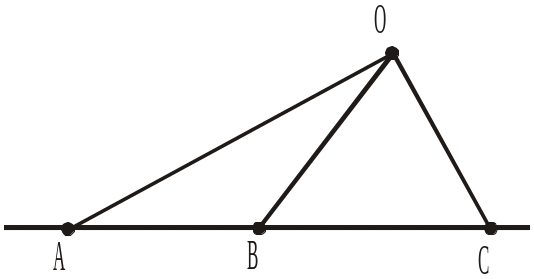 Рис. 278
Рис. 278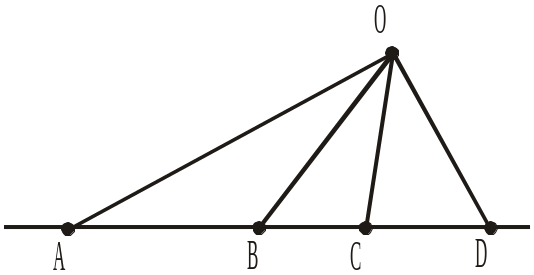 Рис. 279
Рис. 279