- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Третій ступінь високого рівня (бал 12)
1. Між сторонами кута (ab), що дорівнює 60°, проходить промінь с. Знайти градусну міру кута (ас), якщо 3(ас) + 2(cb) = 140°.
2. Між сторонами прямого кута (ab) проходить промінь d. Знайти градусну міру кутів (аd) і (bd), якщо 4(аd) + 3(bd) = 280°.
3. Між сторонами розгорнутого кута (aа1) проходить промінь m. Знайти градусну міру кутів (аm) і (ma1), якщо 5(аm) + 2(ma1) = 600°.
4. Між сторонами кута AOB, що дорівнює 40°, проходить промінь ОС. Знайти градусну міру кутів АОС і ВОС, якщо 5АОС + 2ВОС = 110°.
1. n = 51. 2. n = 10. 3. n = 6. |
|
4. Скільки нерозгорнутих кутів утворюють шість прямих, що перетинаються в одній точці?
7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
1. Як називається фігура, що складається з точок А, В і С, що не лежать на одній прямій, і трьох відрізків АВ, ВС і АС, які попарно сполучають ці точки? 2. Як називаються у трикутнику АВС точки А, В і С? 3. Як називаються у трикутнику АВС відрізки АВ, ВС і АС? |
|
4. Чим є для трикутника АВС фігура, утворена променями АВ і АС; ВА і ВС; СВ і СА?
5. За якими елементами позначають трикутник?
6. Який знак вживають замість слова «трикутник»?
1) вершини; 2) сторони; 3) кути; 4) сторону, що лежить проти кута: М; О; K; |
|
5) кут, що лежить проти сторони OK; ОМ; MK;
6) трьома буквами кути, що прилягають до сторони МK; ОK; OM;
7) кут між сторонами: а) ОМ і KM; б) MO і KO; в) MK і OK;
8) сторони, що прилягають до кута М; кута О; кута K.
За записом «АВС» назвати:
1) вершини трикутника;
2) сторони трикутника;
3) кути трикутника;
4) сторони, що лежать проти кута А; кута В; кута С;
5) кут, що лежить між сторонами: АВ і АС; АВ і ВС; АС і СВ;
6) кути, що прилягають до сторони: ВС; АВ; АС;
7) кути, що лежать проти сторони: АВ; ВС; АС.
Схематично (від руки) зобразити трикутник:
1) з вершинами М, О і K;
2) кути якого А, С і D;
3) дві сторони якого АС і AD, та назвати трикутник;
4) дві сторони якого MO і OP, та назвати трикутник;
5) ABC з тупим кутом А;
6) MOK з прямим кутом М.
|
|
2. Як називаються фігури, зображені на рисунку 265, а)–г)?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 265
3. Як називається фігура, яка складається із трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки? 4. Як називаються у трикутнику АBC: точки А, В і С; відрізки АВ, BC і АС (рис. 266)? |
|
5. Який кут лежить проти сторони АВ у трикутнику АBC (рис. 266)?
6. Яка сторона у трикутнику АВС лежить проти кута В (рис. 266)?
1. Як називаються два трикутники, якщо три кути і протилежні їм сторони одного трикутника дорівнюють відповідно трьом кутам і протилежним їм сторонам другого трикутника?
2. Як називаються два трикутники, якщо три сторони і протилежні їм кути одного трикутника дорівнюють відповідно трьом сторонам і протилежним їм кутам другого трикутника?
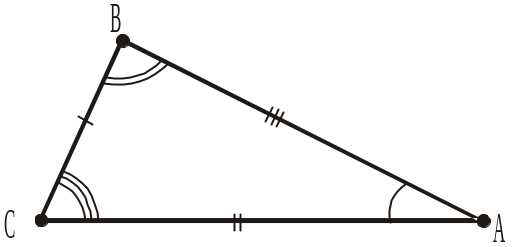
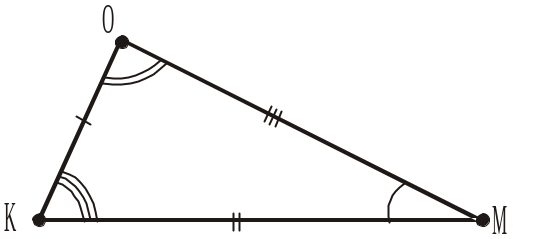
3. Як називаються трикутники АВС і MOK (рис. 338), якщо A = M, B = O, C = K і ВС = OK, AC = MK, AB = MO?
|
|
Рис. 267
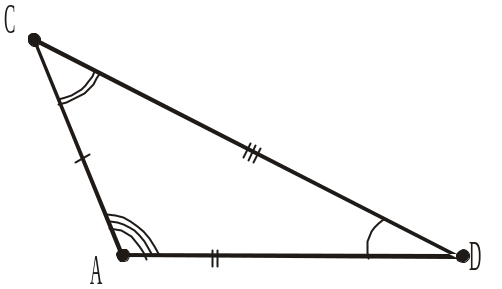
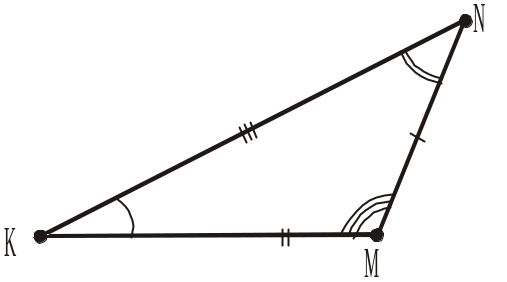
4. Якими є трикутники ACD і MNK (рис. 268), якщо AC = MN, CD = NK, AD = MK, D = K, A = M, C = N?
|
|
Рис. 268

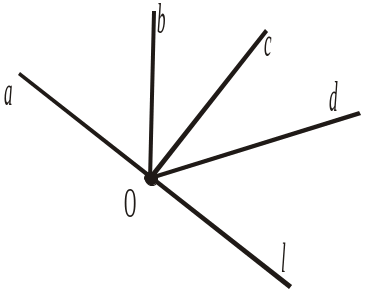 Рис. 261
Рис. 261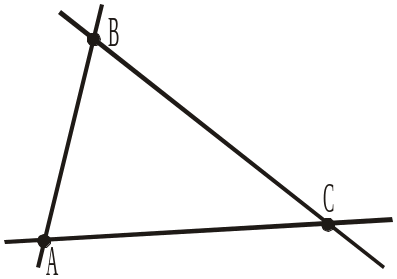 Рис. 262
Рис. 262 Рис. 263
Рис. 263
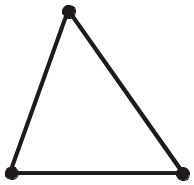

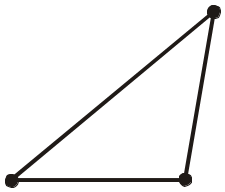
 Рис. 266
Рис. 266