
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
1. Поточний бал за перевірку досягнень на початковому рівні, яка проводиться відразу після вивчення теорії, виставляється в зошит і не виставляється в журнал і щоденник.
2. Поточні бали (оцінки) за проміжні успіхи учнів на середньому і достатньому рівнях виставляються в зошиті, а в журнал і щоденник — тільки за бажанням учнів.
3. За теми, на вивчення яких відводиться 1 год, або які вивчаються неповно чи оглядово, оцінка виставляється тільки за бажанням учня.
4. За теми, на вивчення яких відводиться 2–3 год, тематична (підсумкова) оцінка виставляється на основі перевірочної роботи та домашніх перевірочних і самостійних робот.
5. За теми, на вивчення яких відводиться 4 год, тематична оцінка виставляється за результатами контрольної роботи, в окремих випадках вона може бути підвищена на 1 бал за результатами поточного оцінювання.
Посібник можна використовувати і для проведення тематичних контрольних робіт. Із завдань, що входять до тематичного оцінювання, формуються варіанти робіт середнього, достатнього і високого рівнів. У кожний варіант рекомендуємо включати два завдання нижчого ступеня і по одному із двох інших ступенів.
Тематичне оцінювання за кількома темами чи розділами, як підтверджувальне, проводиться на основі результатів вивчення тем, що входять до тематичного оцінювання. Учневі рекомендується виконувати завдання того рівня, якому переважно відповідають оцінки за теми. При цьому нижчий бал кожного рівня гарантується автоматично. Учень може обрати для тематичного оцінювання і рівень, вищий від рекомендованого вчителем. У цьому випадку при невиконанні завдань вищий бал попереднього рівня йому не гарантується.
Оцінювання виконання тематичних робіт проводиться за кількістю правильно розв’язаних задач відповідно до викладених критеріїв для перевірочних робіт. Якщо учень правильно виконав усі завдання визначеного вчителем рівня і деякі завдання наступного рівня, то оцінка виставляється за кількістю правильно виконаних завдань вищого рівня. Якщо учень правильно виконав завдання вищого рівня, але не виконав чи припустився помилки в завданні вихідного для нього рівня, то завдання вищого рівня зараховуються йому як завдання вихідного.
Якщо учень, атестуючись на середньому рівні, не отримав балів, то йому виставляється оцінка за результатами перевірок початкового рівня у процесі вивчення тем або повторно проводиться така ж перевірка.
Кожен учень має право на перездачу тематичного оцінювання на вищий рівень або на вищий бал рівня від того, на якому він оцінювався. Перездача проводиться у визначений учителем час.
Розділ І. Основні властивості найпростіших геометричних фігур
1. Властивості належності точок і прямих
Початковий рівень
Перший ступінь початкового рівня (бал 1)
1. Які з наведених математичних об’єктів є геометричними фігурами?
а) Натуральні числа; б) точка; в) звичайні дроби; г) відрізок; д) рівняння; е) пряма.
2. Як називається наука про властивості геометричних фігур?
3. Як називається розділ геометрії, в якому вивчаються геометричні фігури на площині?
4. Як називається фігура, зображена на рисунку 1? 5. Як називається фігура, зображена на рисунку 2? 6. Які геометричні фігури вважають основними на площині? 7. Про яку з геометричних фігур Евклід говорив, що «це те, що не має частин»? 8. З яких геометричних фігур складена пряма? 9. Якою уявляють пряму? |
|
|
а) Обмеженою; б) необмеженою.
10. Геометричні рисунки прямої є зображенням усієї прямої чи її частини?
11. Чи вважають геометричними фігурами частини або об’єднання геометричних фігур?
12. Яка з наведених фігур є частинами прямої?
а) Відрізок; б) коло; в) трикутник; г) квадрат.
|
|
|
|
|
Рис. 3 |
Рис. 4 |
Рис. 5 |
|
|
|
|
|||
Рис. 6 |
Рис. 7 |
|||
Назвати:
1) точку, що належить прямій a (рис. 3);
2) точку, що не належить прямій а (рис. 3);
3) точку, що лежить на прямій b (рис. 4);
4) точку, що не лежить на прямій b (рис. 4);
5) точку, через яку не проходить пряма с (рис. 5);
6) точку, через яку проходить пряма с (рис. 5);
7) дві точки, через які проходить пряма a (рис. 6);
8) дві точки, через які не проходить пряма a (рис. 6);
9) три точки, що належать прямій c (рис. 7);
10) три точки, що не належать прямій c (рис. 7).
1. Як розміщена точка А відносно прямої а на рисунках 8, а)–г)?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 8
2. Як розміщена точка А відносно прямої b на рисунках 9, а)–г)?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 9
3. Як розміщена пряма m відносно точки K на рисунках 10, а)–г)?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 10
4. Як розміщена пряма b відносно точки K на рисунках 11, а)–г)?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 11
1) Як розміщена точка А відносно прямої a; прямої b? 2) Як розміщена точка B відносно прямої b; прямої a? 3) Як розміщена точка С відносно прямої a; прямої b? 4) Як розміщена точка О відносно прямої a; прямої b? 5) Як називається точка О, що належить прямій a і прямій b? |
|
6) У якій точці перетинаються прямі а і b?
7) Як називають спільну точку двох прямих?
8) Як називають точку, через яку проходять дві різні прямі?
Схематично (від руки) зобразити (1–10):
1) пряму CD;
2) пряму с і точку А, що їй належить;
3) точку Р і пряму b, що проходить через неї;
4) пряму m і точку, що їй не належить;
5) точку С і пряму m, що не проходить через неї;
6) точки С і D та пряму, що проходить через них;
7) точки А і С та пряму, якій вони обидві належать;
8) прямі b і c, що перетинаються;
9) прямі m і n, що перетинаються в точці K;
10) прямі а і с та точку О їхнього перетину.

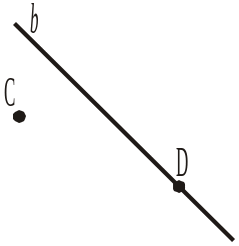
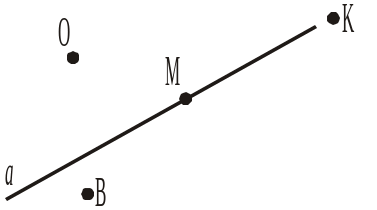
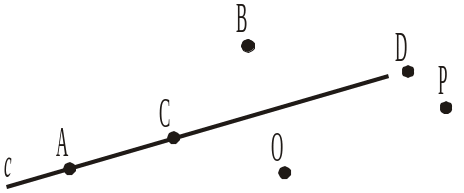






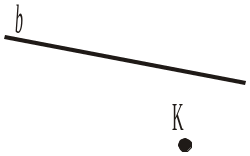
 Рис. 12
Рис. 12