- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Третій ступінь початкового рівня (бал 3)
|
|
1. АОР = ....
а) 15°; б) 5°; в) 10°;
2. АОС = ....
а) 50°; б) 55°; в) 45°;
3. АОD = ....
а) 80°; б) 85°; в) 75°;
4. АОM = ....
а) 115°; б) 120°; в) 125°;
5. АОN = ....
а) 155°; б) 170°; в) 160°.
|
|
а) Більша від 60°; б) менша від 60°; в) 60°.
2. Промінь AD, що проходить між сторонами кута BAC, ділить його на два кути так, що CAD = 20° і BAD = 110° (рис. 199). Чому дорівнює градусна міра кута ВАС? |
|
а) 110° – 20°; б) 110° + 20°; в) ![]() .
.
3. Промінь m (рис. 200) проходить між сторонами кута (ab). (am) = 25, (bm) = 35. Чому дорівнює градусна міра кута (ab)? а) 60; б) 10; в) 100. |
|
4. Промінь, що проходить між сторонами кута, ділить його на частини, градусна міра яких 30 і 40. Чому дорівнює градусна міра даного кута?
а) 40 + 30; б) 40 – 30; в) 2·(40 + 30).
5. Промінь, що проходить між сторонами кута А, ділить його на кути 35° і 45°. Чому дорівнює градусна міра кута А?
а) 35 + 45; б) 45 – 35;
в) ![]() ; г) не
можна визначити.
; г) не
можна визначити.
а) 75 + 20; б) 75 – 20; |
|
в) 90 – 20; г) не можна визначити.
2. На рисунку 202 АОС = 125°, промінь OD утворює зі стороною ОС кут DOC, що дорівнює 80°. Чому дорівнює градусна міра кута AOD? |
|
а) 125 + 80; б) 125 – 80; в) не можна визначити.
3. Від променя AD в одну півплощину відносно прямої AD відкладено кут MAD, що дорівнює 35°, і кут CAD, що дорівнює 100° (рис. 203). Чому дорівнює градусна міра кута САМ? |
|
4. Від променя a в одну півплощину відкладено кути (ba) і (ca) (рис. 204). Чому дорівнює кут між променями b і c? а) 80° + 30°; б) 80° – 30°; в) 100° – 30°. |
|
5. Від променя ОА в одну півплощину відносно прямої ОА відкладено кути ВОА і СОА (рис. 205). Чому дорівнює градусна міра кута між променями ОС і ОВ? а) 150; б) 70°; в) 80°. |
|
6. Від променя m в одну півплощину відкладено кути (mk) і (mn) (рис. 206). Чому дорівнює градусна міра кута (nk), що доповнює кут (km) до кута (mn)? а) 80°; б) 60°; в) 20°; г) 140°. |
|
а) 200° – 40°; б) 180° – 40°; в) 180° + 40°; г) не можна визначити. |
|
2. Промінь b проходить між сторонами розгорнутого кута (ас) і утворює зі стороною a кут (ab), що дорівнює 35° (рис. 208). Чому дорівнює кут (bc), що утворює промінь b зі стороною с? |
|
а) 180° – 35°; б) 180° + 35°;
в) 200° – 35°; г) не можна визначити.
3. Промінь ОС проходить між сторонами розгорнутого кута AOD і утворює зі стороною OA кут АОС, що дорівнює 130° (рис. 209). Чому дорівнює кут COD, що утворює промінь OC зі стороною OD даного розгорнутого кута? |
|
4. Промінь, що проходить між сторонами розгорнутого кута, утворює з однією із його сторін кут 70°. Який кут утворює цей промінь з іншою стороною кута?
1. Скільки кутів із градусною мірою 30° можна відкласти від променя а у верхню півплощину? |
|
а) Більше, ніж один; б) один або жодного; в) один і тільки один.
2. Скільки кутів з градусною мірою 30° можна відкласти від променя у нижню півплощину?
а) Більше, ніж один; б) один або жодного; в) один і тільки один.
3. Скільки всього кутів з градусною мірою 30° можна відкласти від променя а?
а) Два; б) один і тільки один; в) більше, ніж два.
4. Скільки кутів заданої градусної міри, меншої від 180°, можна відкласти від одного променя?
а) Один і тільки один; б) два; в) більше, ніж два.
5. Скільки кутів заданої градусної міри, меншої від 180°, можна відкласти від будь-якого променя в одну півплощину?
а) Один і тільки один; б) два; в) більше, ніж два.
|
|
1. Градусна міра якого з кутів (ab) чи (ас) менша?
2. Який із променів — b чи c — проходить між сторонами кута, утвореного променем а і іншим з цих променів?
а) Промінь с проходить між сторонами кута (ас);
б) промінь b проходить між сторонами кута (ас).
3. Сторона якого з кутів — з більшою чи з меншою градусною мірою — проходить між сторонами іншого кута?
Від променя a відкладено в одну півплощину кути (am) і (ad). Який із променів m (рис. 212а) чи d (рис. 212б) проходить між сторонами іншого кута, якщо: |
|
|
4. (am) = 30°, (ad) = 100°;
5. (am) = 75°, (ad) = 150°;
6. (am) = 150°, (ad) = 100°;
7. (am) = 90°, (ad) = 120°.
Від променя a в різні півплощини відкладено кути (ab) і (ac). На якому з рисунків 213, а)–б):
|
|
а) |
б) |
Рис. 213
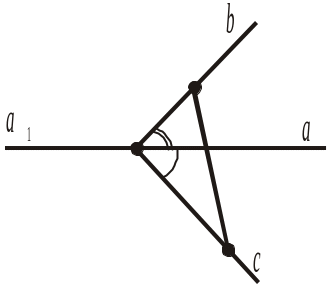
1) промінь a проходить між сторонами кута (bc);
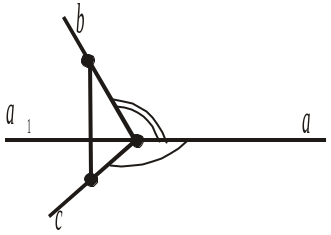
2) промінь a1 — доповняльний до променя а — проходить між сторонами кута (bc);
3) градусна міра кута (bc) дорівнює сумі градусних мір кутів (ab) і (ас);
4) градусна міра кута (bc) дорівнює сумі градусних мір кутів (a1b) і (а1с);
5) сума градусних мір кутів (ab) і (ас) більша від градусної міри розгорнутого кута, тобто від 180°;
6) сума градусних мір кутів (ab) і (ас) менша від градусної міри розгорнутого кута, тобто від 180°?
7. Який із променів а чи а1 проходить між сторонами кута (bc), якщо сума градусних мір кутів (ab) і (ас) менша від 180° (рис. 213)?
8. Який із променів а чи а1 проходить між сторонами кута (bc), якщо сума градусних мір кутів (ab) і (ас) більша від 180° (рис. 213)?

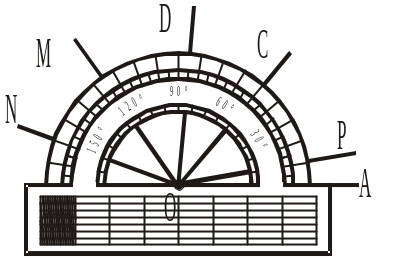 Рис. 197
Рис. 197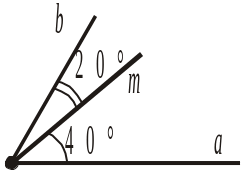 Рис. 198
Рис. 198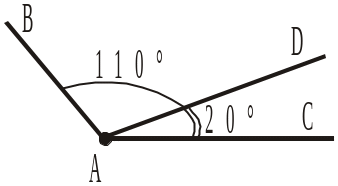 Рис. 199
Рис. 199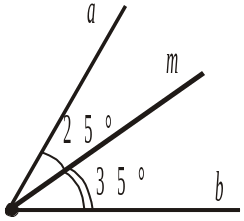 Рис. 200
Рис. 200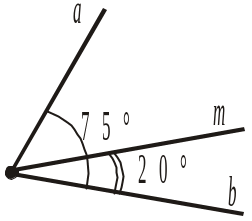 Рис. 201
Рис. 201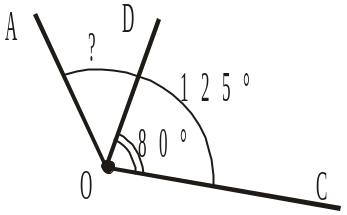 Рис. 202
Рис. 202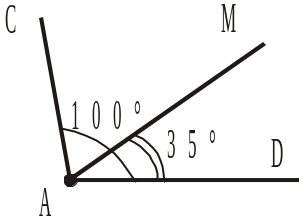 Рис. 203
Рис. 203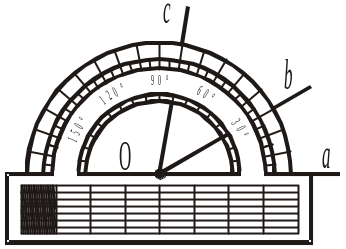 Рис. 204
Рис. 204 Рис. 205
Рис. 205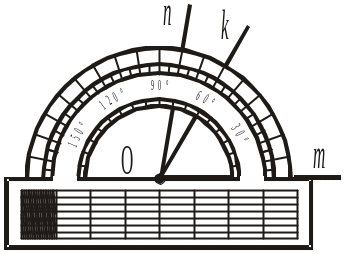 Рис. 206
Рис. 206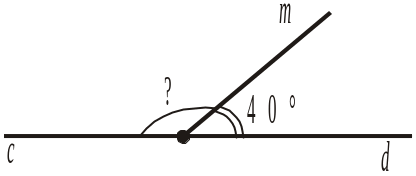 Рис. 207
Рис. 207 Рис. 208
Рис. 208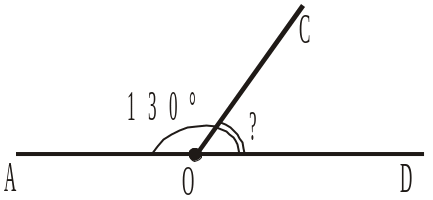 Рис. 209
Рис. 209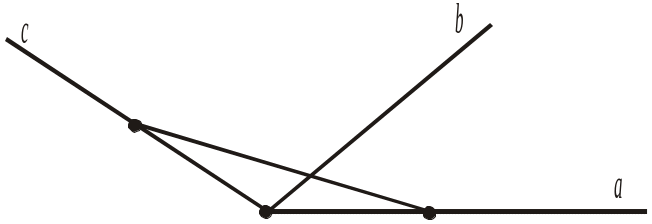 Рис. 211
Рис. 211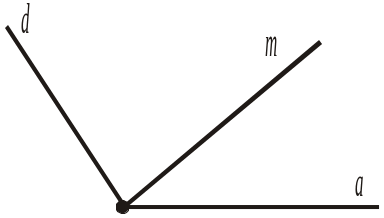 Рис. 212а
Рис. 212а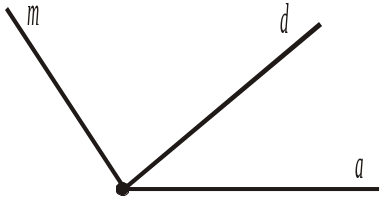 Рис. 212б
Рис. 212б