
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Другий ступінь початкового рівня (бал 2)
1. На яких з рисунків 184, а)–г) промені а і b утворюють кут?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 184
2. На яких з рисунків 185, а)–г) промені c і d утворюють кут?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 185
1) зі стороною а; 2) зі стороною с; 3) зі стороною d; 4) на які ділить промінь с кут (ad). |
|
Назвати на рисунку 187 кути: 5) зі стороною OD; 6) зі стороною OC; 7) зі стороною OA; 8) на які ділить промінь OC кут AOD. |
|
Назвати на рисунку 188 кути: 9) зі стороною OA; 10) зі стороною OD; 11) зі стороною OC; 12) на які ділить промінь OD кут AOC.
Фігура, що складається... |
|
а) із трьох променів зі спільною початковою точкою;
б) із двох різних променів, що перетинаються;
в) із двох різних променів зі спільною початковою точкою.
2. Яка з наведених фігур є розгорнутим кутом?
Фігура, утворена...
а) будь-якими двома променями однієї прямої;
б) двома різними променями однієї прямої, що мають спільну початкову точку;
в) будь-якими двома різними променями однієї прямої, що не мають спільної точки.
3. Яка з наведених фігур називається розгорнутим кутом?
Фігура, утворена...
а) будь-якими двома променями;
б) двома доповняльними променями;
в) двома різними променями, що утворюються при перетині двох прямих.
На якому з рисунків 189, а)–г):
1) промінь а проходить між сторонами кута (bc);
2) промінь b проходить між сторонами кута (ac);
3) промінь c проходить між сторонами кута (ab);
4) жоден із променів не проходить між сторонами кута, утвореного двома іншими променями?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 189
На якому з рисунків 190, а)–г):
5) промінь ОА проходить між сторонами кута ВОС;
6) промінь ОВ проходить між сторонами кута АОС;
7) промінь ОС проходить між сторонами кута АОВ;
8) жоден із променів не проходить між сторонами кута, утвореного двома іншими променями?
|
|
|
|
а) |
б) |
в) |
г) |
Рис. 190
1. Як називається кут, прийнятий за одиницю вимірювання всіх інших кутів?
а) Процентом; б) метром;
в) градусом; г) фунтом.
2. Яку частину від розгорнутого кута становить кут, названий градусом?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3. Чому дорівнює градусна міра розгорнутого кута?
4. Яким числом є градусна міра кута?
а) Додатним; б) невід’ємним; в) додатним або від’ємним.
5. Чи існують кути, що не мають градусної міри?
6. Доповнити запис основної властивості вимірювання кутів.
Кожний кут має певну градусну міру, ...
а) меншу від нуля;
б) більшу від нуля;
в) більшу від нуля або рівну нулю.
7. Доповнити запис основної властивості вимірювання розгорнутих кутів.
Градусна міра розгорнутого кута дорівнює...
а) 90°; б) 100°; в) 180°.
8. Чому дорівнює градусна міра розгорнутого кута за його основною властивістю?
9. Якою може бути градусна міра нерозгорнутого кута?
а) Будь-яким додатним числом;
б) додатним числом, меншим від 180°.
10. Чи існують кути з градусною мірою, більшою від 180°?
11. Доповнити запис до істинного твердження.
Градусна міра будь-якого кута...
а) не більша від 200° (менша або дорівнює 200°);
б) більша від 180°;
в) не більша від 180° (менша або дорівнює 180°);
г) менша від 180°.
1) 120°; 2) 150°; 3) 90°; 4) 30°; 5) 60°. |
|
1. Якими є кути А і В, якщо А = 30° і В = 30°?
а) Рівними; б) нерівними.
2. Як називаються два кути А і В, якщо вони мають однакову градусну міру?
3. (ab) = 130°, (bc) = 130°. Як називаються кути (ab) і (bc)?
4. А = 30°, С = 50°. Який з кутів більший?
а) А; б) С; в) не можна визначити.
5. Доповнити запис.
Із двох кутів більший той, у якого градусна міра...
а) менша; б) більша.
6. Доповнити запис.
Із двох кутів менший той, у якого градусна міра...
а) менша; б) більша.
|
|
а) Більша від 40°; б) менша від 40°;
в) дорівнює 40°; г) не можна визначити.
2. Промінь ОМ проходить між сторонами кута ВОА (рис. 193). Сума градусних мір кутів ВОМ і АОМ дорівнює 100°. Чому дорівнює градусна міра кута АОВ? |
|
а) Більша від 100°; б) менша від 100°;
в) дорівнює 100°; г) не можна визначити.
3. Доповнити запис основної властивості вимірювання кутів.
Сума градусних мір кутів, на які розбивається кут будь-яким променем, що проходить між його сторонами, ...
а) дорівнює градусній мірі кута;
б) більша від градусної міри кута;
в) менша від градусної міри кута.
4. Якими є градусна міра кута і сума градусних мір кутів, на які кут розбивається будь-яким променем, що проходить між його сторонами?
а) Рівними; б) нерівними;
в) не можна визначити: можуть бути рівними, а можуть бути і нерівними.
5. Доповнити запис основної властивості вимірювання кутів.
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається...
а) будь-яким променем, що проходить між його сторонами;
б) тільки деякими променями, що проходять між його сторонами.
а) Один і тільки один (відкладений); б) два; в) більше, ніж один. |
|
2. На рисунку 195 від променя ОА у нижню півплощину відносно прямої ОА відкладено кут DОА, що дорівнює 60°. Скільки всього кутів, що дорівнюють 60°, можна відкласти від променя ОА в дану півплощину? а) Два; б) один і тільки один (відкладений); в) більше, ніж один. |
|
3. На рисунку 196 від променя ОА в одну з півплощин відносно прямої ОА відкладено кут, що дорівнює 90°. Чи можна відкласти від променя ОА в дану півплощину інший кут, що дорівнює 90°? |
|
4. Скільки можна відкласти від даного променя в дану півплощину кутів, що дорівнюють 120°?
а) Один і тільки один; б) два; в) більше, ніж два.
5. Доповнити запис основної властивості відкладання кутів.
Від будь-якого променя в дану півплощину можна відкласти з даною градусною мірою, меншою від 180°, ...
а) більше, ніж один кут;
б) один або жодного кута;
в) один і тільки один кут.
6. Скільки можна відкласти від будь-якого променя у дану півплощину кутів з даною градусною мірою, меншою від 180°?
а) Більше, ніж один;
б) один або жодного;
в) один і тільки один.
7. Скільки можна відкласти від даного променя у дану півплощину кутів, що дорівнюють 100°?






 Рис. 186
Рис. 186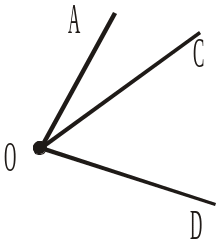 Рис. 187
Рис. 187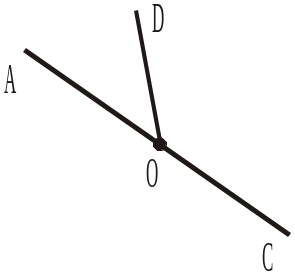 Рис. 188
Рис. 188

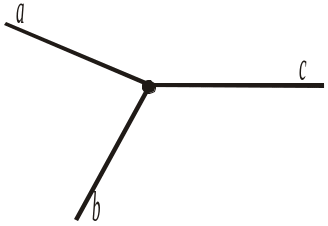
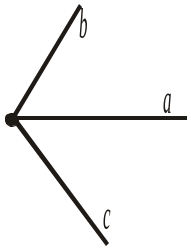
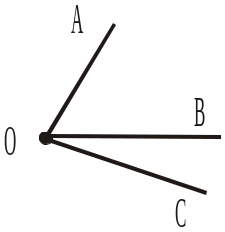
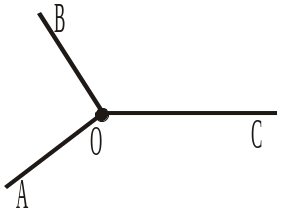
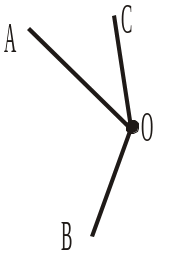
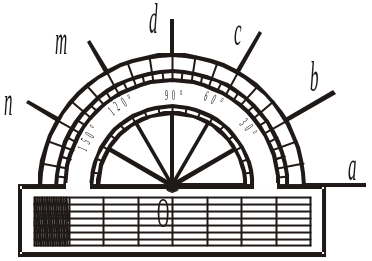 Рис. 191
Рис. 191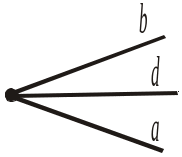 Рис. 192
Рис. 192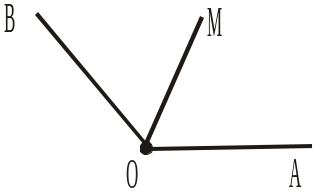 Рис. 193
Рис. 193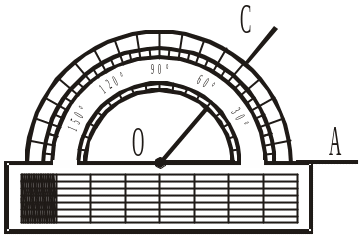 Рис. 194
Рис. 194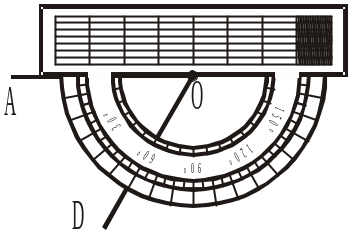 Рис. 195
Рис. 195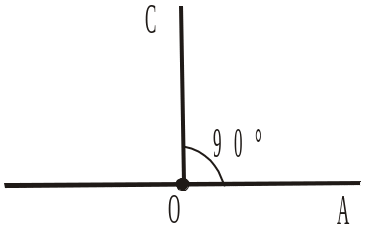 Рис. 196
Рис. 196