
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Високий рівень Перший ступінь високого рівня (бал 10)
1. Зобразити точки С і D, відстань між якими 5 см. Побудувати точки, що розміщені від точки С на відстані 3 см, а від точки D — на відстані 4 см. Сполучити побудовані точки відрізками з точками С і D.
2. Зобразити точки М і N, відстань між якими 4 см. Побудувати точки, що розміщені від точки M на відстані 5 см, а від точки N — на відстані 3 см. Сполучити побудовані точки відрізками з точками М і N.
3. Зобразити точки А і D, відстань між якими 4 см. Побудувати точки, що розміщені від точки A і від точки D на відстані 5 см. Сполучити побудовані точки відрізками з точками А і D.
4. Зобразити точки М і K, відстань між якими 3,6 см. Побудувати точки, що розміщені від точки M на відстані 4 см, а від точки K — на відстані 4,5 см. Сполучити побудовані точки відрізками з точками М і K.
Побудувати систему координат. Позначити точку А. Побудувати фігуру, яку утворюють усі точки координатної площини, що розміщені від точки А на відстані d одиничних відрізків (1–4):
1. А(–3; 2), d = 4. 2. А(4; 5), d = 5.
3. А(6; 0), d = 6. 4. А(0; 0), d = 3.
Побудувати систему координат.
1. Позначити точку А(1; 1) і шість точок, що розміщені від неї на відстані 6 одиничних відрізків.
2. Позначити точку С(–1; 2) і вісім точок, що розміщені від неї на відстані 8 одиничних відрізків.
3. Позначити точку М(–3; –2) і сім точок, що розміщені від неї на відстані 10 одиничних відрізків.
4. Позначити точку K(4; –2) і п’ять точок, що розміщені від неї на відстані 7 одиничних відрізків.
Другий ступінь високого рівня (бал 11)
|
|
1) має з першим колом тільки одну спільну точку. Скільки розв’язків має задача? Чому дорівнюють радіуси таких кіл?
2) має з першим колом дві спільні точки. Скільки таких кіл можна побудувати? Чому дорівнюють радіуси таких кіл?
3) має з першим колом дві спільні точки і радіус якого дорівнює цілому числу сантиметрів. Скільки таких кіл можна побудувати? Записати їхні радіуси.
4) не перетинає перше коло, а радіус його менший від довжини відрізка АВ і дорівнює цілому числу сантиметрів. Скільки існує таких кіл? Записати їхні радіуси.
Побудувати систему координат. Заштрихувати частину площини, яку утворюють усі точки, що розміщені від точки В на відстані, більшій, ніж d одиничних відрізків (1–4), якщо:
1. В(0; 0), d = 4. 2. В(1; 1), d = 3.
3. В(3; –2), d = 4. 4. В(–4; 2), d = 5.
Побудувати систему координат. Заштрихувати частину площини, яку утворюють усі точки, що розміщені від точки А на відстані, меншій, ніж d одиничних відрізків (1–4), якщо:
1. А(3; 2), d = 3. 2. А(5; 1), d = 4.
3. А(–2; 0), d = 5. 4. А(0; 0), d = 10.
Побудувати систему координат і коло з центром у початку координат радіусом 5 одиничних відрізків. Заштрихувати частину вказаної координатної чверті, яку утворюють усі її точки, що розміщені на відстані d (1–4) від початку координат:
1) І чверть, d < 5; 2) ІІ чверть, d > 5;
3) IIІ чверть, d > 5; 4) ІV чверть, d < 5.

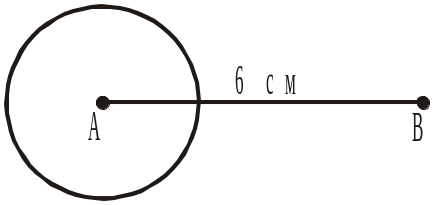 Рис. 115
Рис. 115