
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Другий ступінь високого рівня (бал 11)
Точки А, В і С, що не лежать на одній прямій, послідовно сполучено відрізками АВ, ВС і СА. Довести (1–4), що коли пряма, яка не проходить через точки А, В і С, ...
1) перетинає відрізок АВ, то вона перетинає або відрізок ВС, або відрізок АС;
2) перетинає відрізки АВ і ВС, то вона не перетинає відрізок АС;
3) не перетинає відрізки АВ і АС, то вона не перетинає відрізок ВС;
4) не перетинає відрізки АС і ВС, то вона не перетинає відрізок АВ.
|
|
1) в одній півплощині як відносно прямої а, так і відносно прямої b;
2) в одній півплощині відносно прямої а і в різних півплощинах відносно прямої b;
3) у різних півплощинах відносно прямої а і в одній півплощині відносно прямої b;
4) у різних півплощинах відносно прямої а і в різних півплощинах відносно прямої b.
Третій ступінь високого рівня (бал 12)
Дано пряму а і декілька точок, що не належать цій прямій. Кожну пару точок сполучено відрізком. Скільки з даних відрізків перетинають пряму, а скільки — не перетинають, якщо:
1) одна точка лежить в одній півплощині, а п’ять точок — в іншій півплощині відносно прямої а;
2) дві точки лежать в одній півплощині, а чотири точки — в іншій півплощині відносно прямої а;
3) чотири точки лежать в одній півплощині, а шість точок — в іншій півплощині відносно прямої а;
4) п’ять точок лежать в одній півплощині, а п’ять — в іншій півплощині відносно прямої а?
4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
2. Як називається фігура (рис. 110), яка складається з усіх точок площини, що розміщені на відстані 5 см від даної точки О?
3. Як називається фігура, яка складається з усіх точок площини, що розміщені на однаковій відстані від даної точки? 4. Як називається фігура, яка складається з усіх точок площини, що розміщені на відстані 10 км від даної точки М? 5. Як називається точка, від якої розміщені на однаковій відстані всі точки кола? |
|
|
|
1) відрізок ОА, що сполучає центр кола О і точку А на колі; 2) відрізок CD, що сполучає точки С і D кола та проходить через центр кола точку О; 3) число, що дорівнює відстані між точками О і А; |
|
4) число, що дорівнює відстані між точками D і C?
Другий ступінь початкового рівня (бал 2)
1. Яка з наведених фігур називається колом?
Фігура, яка складається з...
а) декількох точок площини, що розміщені на однаковій відстані від даної точки;
б) нескінченної кількості точок;
в) усіх точок площини, що розміщені на однаковій відстані від даної точки.
2. Яка з наведених фігур називається колом?
Фігура, яка складається з усіх точок площини, які розміщені на однаковій відстані...
а) від даної прямої; б) від даних двох прямих;
в) від даної точки; г) від двох даних точок.
3. Яка з наведених фігур є колом з центром у точці О радіуса 5 см?
Фігура, яка складається з...
а) усіх точок площини, які розміщені на відстані 2,5 см від точки О;
б) деяких точок площини, які розміщені на відстані 5 см від точки О;
в) усіх точок площини, які розміщені на відстані 5 см від точки О;
4. Яка з наведених фігур називається радіусом кола?
а) Відрізок, що сполучає дві точки кола;
б) пряма, що перетинає коло;
в) пряма, що проходить через центр кола;
г) відрізок, що сполучає центр кола і точку на ньому.
5. Яке з наведених чисел називають радіусом кола?
Число, що дорівнює відстані між...
а) двома будь-якими точками кола;
б) центром і точкою на колі;
в) деякими двома точками кола.
6. Який з наведених відрізків називають діаметром кола?
Відрізок, що сполучає...
а) дві точки кола;
б) центр кола і точку на ньому;
в) дві точки кола і проходить через центр кола;
г) дві точки кола і не проходить через центр кола.
1) довжина відрізка ОВ; 2) довжина відрізка АВ; 3) діаметр кола; 4) довжина відрізка ОМ? |
|
М, Р і K — точки кола радіуса 6 см з центром у точці О. Чому дорівнює довжина відрізка:
1) ОР; 2) ОМ;
3) MK, якщо точки М, K і О лежать на одній прямій;
4) MP, якщо пряма МР проходить через точку О?

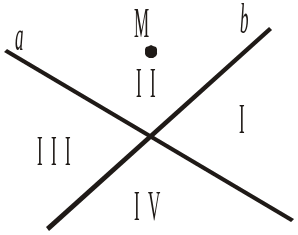 Рис. 108
Рис. 108 Рис. 109
Рис. 109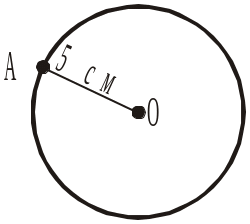 Рис. 110
Рис. 110 Рис. 111
Рис. 111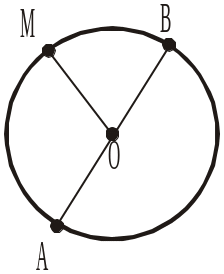 Рис. 112
Рис. 112