
- •Анатолій Капіносов Посібник для рівневого навчання з геометрії
- •Передмова
- •Особливості посібника і технологія його використання
- •Деякі рекомендації щодо оцінювання навчальних досягнень учнів з теми, що випливають з особливостей 12-бальної шкали
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Обґрунтування
- •Обґрунтування
- •Третій ступінь високого рівня (бал 12)
- •2. Відрізок. Вимірювання відрізків Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Розв’язання
- •Розв’язання
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Розв’язання (повний запис)
- •Розв’язання (короткий запис)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •3. Півплощини Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •4. Коло: Означення Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •5. Промінь Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другій ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Гострий, прямий і тупий кути. Бісектриса (підтема 2) Перший ступінь початкового рівня (бал 1)
- •2. Як називається кут аов, градусна міра якого дорівнює 90° (рис. 215)?
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Від променя а (рис. 243) відкласти у верхню півплощину кут (ас), що дорівнює:
- •Другий ступінь середнього рівня (бал 5)
- •Від променя d (рис. 254) відкласти у верхню півплощину кут (dc), що дорівнює:
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •7. Трикутник, рівність трикутників (Означення) Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •8. Паралельні прямі: означення, основна властивість Початковий рівень Перший ступінь початкового рівня (бал 1)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •Другий ступінь початкового рівня (бал 2)
- •Третій ступінь початкового рівня (бал 3)
- •Середній рівень Перший ступінь середнього рівня (бал 4)
- •Другий ступінь середнього рівня (бал 5)
- •Третій ступінь середнього рівня (бал 6)
- •Достатній рівень Перший ступінь достатнього рівня (бал 7)
- •Розв’язання
- •Другий ступінь достатнього рівня (бал 8)
- •Третій ступінь достатнього рівня (бал 9)
- •Високий рівень Перший ступінь високого рівня (бал 10)
- •Другий ступінь високого рівня (бал 11)
- •Третій ступінь високого рівня (бал 12)
- •10. Вертикальні кути. Перпендикулярні прямі Початковий рівень Перший ступінь початкового рівня (бал 1)
Третій ступінь середнього рівня (бал 6)
1. На відрізку АВ завдовжки 32 см взято точку О. Знайти довжину відрізка АО, якщо його довжина на 6 см більша від довжини відрізка ОВ.
2. Точка ділить відрізок завдовжки 48 см на частини, різниця довжин яких дорівнює 8 см. Знайти довжину кожної частини.
3. На відрізку MK завдовжки 26 см взято точку О. Знайти відстань між точками М і О, якщо вона на 8 см менша за відстань між точками О і K.
4. На відрізку АВ завдовжки 46 см взято точку K. Знайти відстань між точками В і K, якщо вона на 12 см більша за відстань між точками А і K.
Завдання-орієнтир
Різниця довжин відрізків АО і ОВ, на які ділить відрізок АВ точка О, дорівнює 3,2 см (рис. 79). Знайти довжину відрізка АО і ВО, якщо АВ = 8,6 см. |
|
Доповнити запис розв’язання задачі.
Розв’язання
Нехай х см — довжина відрізка ОВ (меншого з відрізків АО і ОВ). Тоді _________ (см) — довжина відрізка ОА.
За основною властивістю вимірювання відрізків АО + ОВ = _______.
Складаємо рівняння:
![]() .
.
Розв’язуємо рівняння: _________________, _________________. ОВ = _________, АО = __________.
1. На прямій а зображено точки М, О і K так, що точка О лежить між точками М і K. Відстань між точками М і K дорівнює 48 см. Знайти відстань між точками О і K, якщо вона вдвічі менша, ніж відстань між точками О і М.
2. Довжина відрізка АВ дорівнює 70 см. Точка М відрізка АВ ділить його на відрізки АМ і MB так, що довжина відрізка АМ у 2,5 разу більша від довжини відрізка МВ. Знайти довжину цих відрізків.
3. На відрізку АВ завдовжки 42 см взято точку С. Знайти довжини відрізків АС і BC, якщо вони відносяться як 3 : 4.
4. На якій відстані від кінців відрізка завдовжки 35 см лежить точка, що ділить його у відношенні 2 : 5?
Завдання-орієнтир
На відрізку MK завдовжки 8,4 см взято точку О (рис. 80). Знайти довжини відрізків МО і OK, якщо вони відносяться як 2 : 5. Доповнити запис розв’язання. |
|
Розв’язання
Нехай довжина відрізка МО 2х см, тоді _____ (см) — довжина відрізка OK. За основною властивістю вимірювання відрізка, що ділиться точкою, МО + OK = _____.
Складаємо рівняння:
![]() .
.
Розв’язуємо рівняння: ______________, х = ______. МО = _________, ОK = __________.
Достатній рівень Перший ступінь достатнього рівня (бал 7)
1. На відрізку АВ завдовжки 75 см взято точку О. Знайти довжини відрізків АО і ОВ, якщо довжина відрізка АО становить
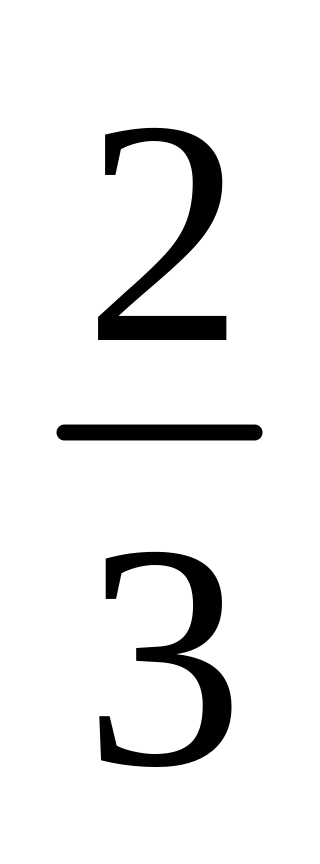 довжини відрізка OB.
довжини відрізка OB.
2. На прямій a взято точки A, B і C
такі, що AC = 56 дм і точка В лежить
між точками А і С. Знайти відстань між
точками А і В, якщо вона становить
![]() відстані між точками В і С.
відстані між точками В і С.
3. На відрізку CD завдовжки 56 дм взято точку О. Знайти довжини відрізків СО і OD, якщо довжина відрізка СО становить 75% довжини відрізка OD.
4. На відрізку CD завдовжки 77 дм
взято точку О. Знайти відстань між
точками О і D, якщо вона становить
![]() відстані між точками О і С.
відстані між точками О і С.
|
|
2. На прямій m позначено точки А і C. Чи може точка M цієї прямої лежати між точками А і С (рис. 82), якщо AM = 10 см, MC = 8 см і AC = 2 см? Відповідь пояснити. |
|
3. На прямій c позначено точки P і O. Чи належить точка М прямої с відрізку РО (рис. 83), якщо РM = 15 см, MО = 3 см і РО = 12 см? Відповідь пояснити. |
|
4. На прямій k позначено точки A і B. Чи належить точка С прямій k відрізку AB (рис. 84), якщо AB = 12 см, AC = 5 см і CB = 8 см. Відповідь пояснити. |
|
Завдання-орієнтир
На прямій с позначено точки А і Р такі, що АР = 7 см. Чи належить точка О прямої c відрізку AР (рис. 85), якщо ОР = 2 см, AО = 9. Відповідь пояснити. |
|

 Рис. 81
Рис. 81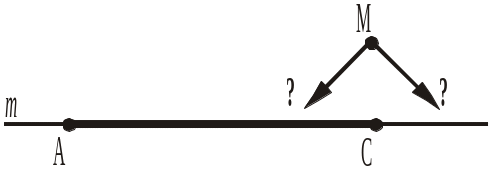 Рис. 82
Рис. 82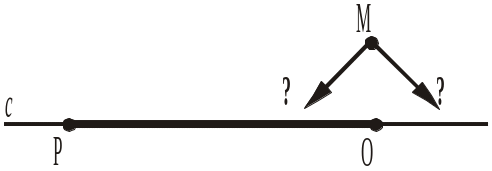 Рис. 83
Рис. 83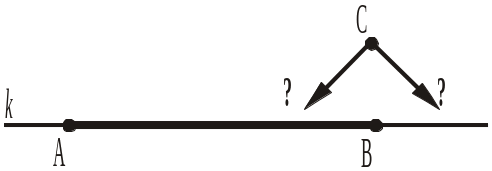 Рис. 84
Рис. 84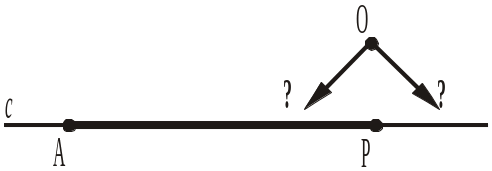 Рис. 85
Рис. 85