Відтворення і застосування теорії Самостійні роботи
№65. Варіант 1.
Середній рівень
1. 1) Дано функцію y = 
.
Знайти значення функції, якщо значення
аргументу дорівнює –2; 5.
2) Дано функцію f(x) = 
.
Знайти значення x, якщо f(x) = –2.
2. Побудувати схематично графік
функції y = 
,
склавши таблицю значень функції для
значень аргументу 1,
2, 4,
8.
3. Задати формулою залежність швидкості v (у км/год) проходження відстані 100 км від часу t (у год). Якою функцією є ця залежність?
Достатній рівень
1. Побудувати графік функції (1–2):
1) y = 
з областю визначення (0; +);
2) 
2. Графіку оберненої пропорційності y = належить точка A(12; –2). Знайти коефіцієнт k.
3. Знайти графічно корені рівняння x2 = –x + 2.
Високий рівень
1. 1) Встановити графічно значення x, за яких функція y = набуває значень, більших від значень функції y = 2.
2) Знайти точки графіка функції
y = 
,
у яких однакові абсциса й ордината.
Побудувати графік функції (2–3):
2. y = 2 – .
3. y = 
.
№66. Варіант 2.
Середній рівень
1. 1) Дано функцію y = –
.
Знайти значення функції, якщо значення
аргументу дорівнює –2; 10.
2) Дано функцію f(x) = 
.
Знайти значення x, якщо f(x) = 2.
2. Побудувати схематично графік
функції y = 
,
склавши таблицю значень функції для
значень аргументу 1,
2, 5,
10.
3. Задати формулою залежність часу t (у год) проходження відстані 200 км від швидкості v (у км/год). Якою функцією є ця залежність?
Достатній рівень
1. Побудувати графік функції (1–2):
1) y = з областю визначення (–; 0);
2) 
2. Графіку оберненої пропорційності y = належить точка A(–3; –7). Знайти коефіцієнт k.
3. Знайти графічно корені рівняння x2 = x + 2.
Високий рівень
1. 1) Встановити графічно значення
x, за яких функція y = 
набуває значень, менших від значень
функції y = 2.
2) Знайти точки графіка функції
y = 
,
у яких абсциса й ордината є протилежними
числами.
Побудувати графік функції (2–3):
2. y = 
.
3. y = 
.
№67. Варіант 3.
Середній рівень
1. 1) Дано функцію y = –
.
Знайти значення функції, якщо значення
аргументу дорівнює –3; 15.
2) Дано функцію f(x) = 
.
Знайти значення x, якщо f(x) = 3.
2. Побудувати схематично графік
функції y = 
,
склавши таблицю значень функції для
значень аргументу 1,
2, 3,
6.
3. Задати формулою залежність довжини прямокутника a (у м), площа якого дорівнює 100 м2, від його ширини b (у м). Якою функцією є ця залежність?
Достатній рівень
1. Побудувати графік функції (1–2):
1) y = з областю визначення (–; 0);
2) 
2. Знайти графічно значення змінної
x, за яких набувають однакових значень
функції y = 
і y = –3x.
3. Графіку оберненої пропорційності
y = 
належить точка A(–12; 12). Встановити,
чи належить графіку точка B(3; –8).
Високий рівень
1. 1) Встановити графічно значення
x, за яких функція y = 
набуває значень, менших від значень
функції y = 2x.
2) Знайти точки графіка функції
y = 
,
розміщені від осі ординат на відстані,
що дорівнює 3.
Побудувати графік функції (2–3):
2. y = 
.
3. y = 
.
№68. Варіант 4.
Середній рівень
1. 1) Дано функцію y = 
.
Знайти значення функції, якщо значення
аргументу дорівнює –4; 16.
2) Дано функцію f(x) = – . Знайти значення x, якщо f(x) = 5.
2. Побудувати схематично графік функції y = , склавши таблицю значень функції для значень аргументу 1, 2, 4.
3. Задати формулою залежність маси овочів (у кг), які можна придбати на 40 грн., залежно від ціни n одного кілограма овочів (у грн.). Якою функцією є ця залежність?
Достатній рівень
1. Побудувати графік функції (1–2):
1) y = – з областю визначення (–; 0);
2) 
2. Знайти графічно значення змінної
x, за яких набувають однакових значень
функції y =
і y = 
.
3. Графіку оберненої пропорційності
y =
належить точка A
.
Встановити, чи належить графіку точка
C
.
Високий рівень
1. 1) Встановити графічно значення x, за яких функція y = набуває значень, більших від значень функції y = .
2) Знайти точки графіка функції
y = 
,
розміщені від осі ординат на відстані,
що дорівнює 8.
Побудувати графік функції (2–3):
2. y = x2 – 1.
3. y = 
.
№69. Варіант 5.
Середній рівень
1. 1) Дано функцію y = 
.
Знайти значення функції, якщо значення
аргументу дорівнює –12; 9.
2) Дано функцію f(x) = 
.
Знайти значення x, якщо f(x) = 6.
2. Побудувати схематично графік функції y = , склавши таблицю значень функції для значень аргументу 1; 2; 4; 8.
3. Знайти значення аргументу x, за яких функції y = і y = набувають рівних значень.
Достатній рівень
1. Побудувати графік функції (1–2):
1) y = x2 з областю визначення (1; +);
2) 
2. Графіку оберненої пропорційності
y =
належить точка A
.
Знайти коефіцієнт k.
3. Розв’язати графічно рівняння x3 = –3x + 4.
Високий рівень
1. 1) Встановити графічно значення x, за яких функція y = набуває значень, менших від значень функції y = –3x.
2) Знайти точки графіка функції
y = 
,
розміщені від осі ординат на відстані,
що дорівнює 20.
Побудувати графік функції (2–3):
2. y = 
.
3. y = 
.
№70. Варіант 6.
Середній рівень
1. 1) Дано функцію y = –
.
Знайти значення функції, якщо значення
аргументу дорівнює –24; 6.
2) Дано функцію f(x) = 
.
Знайти значення x, якщо f(x) = 5.
2. Побудувати схематично графік функції y = , склавши таблицю значень функції для значень аргументу 1; 2; 3; 4; 6; 12.
3. Знайти значення аргументу x,
за яких функції y = 
і y = 
набувають рівних значень.
Достатній рівень
1. Побудувати графік функції (1–2):
1) y = x3 з областю визначення (–; 0);
2) 
2. Графіку прямої пропорційності
y =
належить точка B
.
Знайти коефіцієнт k.
3. Розв’язати графічно рівняння x3 = –2x – 3.
Високий рівень
1. 1) Встановити графічно значення x, за яких функція y = набуває значень, менших від значень функції y = –4x.
2) Знайти точки графіка функції
y = 
,
розміщені від осі абсцис на відстані,
що дорівнює 9.
Побудувати графік функції (2–3):
2. y = 
.
3. y = 
.
Контроль навчальних досягнень учнів
Контрольна робота №7
№71. Варіант 1.
Середній рівень
Побудувати графік функції (1–3):
1. 1) y = 2x; 2) y = –4.
2. 
.
3. y = –
.
Достатній рівень
1. Побудувати графік функції:
1) y = 
з областю визначення [–3; 3] і записати
область її значень;
2) 
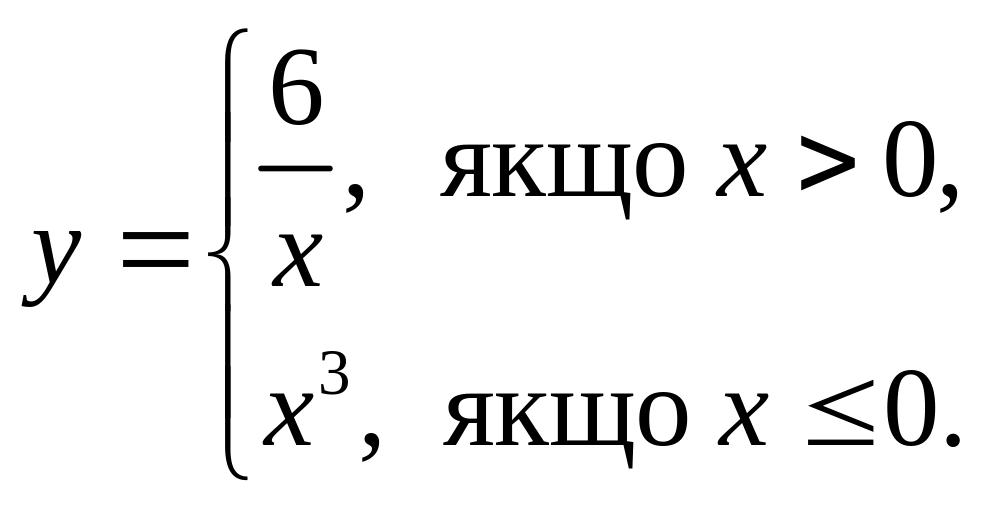
2. Графік лінійної функції y = ax + 5 проходить через точку A(2; 1). Знайти a.
3. Знайти графічно розв’язки рівняння
.
Високий рівень
1. 1) Знайти область визначення функції
і побудувати її графік.
2) Задати функцію без модуля і побудувати її графік.
2. Скласти формулу лінійної функції, графік якої проходить через точки A(0; 5) і B(1; 8).
3. Побудувати графік функції
.
№72. Варіант 2.
Середній рівень
Побудувати графік функції (1–3):
1. 1) y = –4x; 2) y = 7.
2. 
.
3. y = 
.
Достатній рівень
1. Побудувати графік функції:
1) y = 
з областю визначення [–4; 4] і записати
область її значень;
2) 
2. Графік лінійної функції y = 5x + b проходить через точку A(–2; 7). Знайти b.
3. Знайти графічно розв’язки рівняння
.
Високий рівень
1. 1) Знайти область визначення функції
і побудувати її графік.
2) Задати функцію
без модуля і побудувати її графік.
2. Скласти формулу лінійної функції, графік якої проходить через точки A(0; –4) і B(1; –1).
3. Побудувати графік функції
.
№73. Варіант 3.
Середній рівень
Побудувати графік функції (1–3):
1. 1) y = 4x; 2) y = –3.
2. .
3. y = –
.
Достатній рівень
1. Побудувати графік функції:
1) y = 
з областю визначення [–4; 4] і записати
область її значень;
2) 
2. Графіку прямої пропорційності належать точки A(2; –16) і B(–4; m). Знайти значення m.
3. Знайти графічно розв’язки рівняння
.
Високий рівень
1. 1) Знайти область визначення функції
і побудувати її графік.
2) Задати функцію
без модуля і побудувати її графік.
2. Скласти формулу лінійної функції, графік якої проходить через точки A(1; 4) і B(2; 7).
3. Побудувати графік функції
.
№74. Варіант 4.
Середній рівень
Побудувати графік функції (1–3):
1. 1) y = –3x; 2) y = 2.
2. 
.
3. y = 
.
Достатній рівень
1. Побудувати графік функції:
1) y = 
з областю визначення [–3; 3] і записати
область її значень;
2) 
2. Графіку прямої пропорційності належать точки A(3; 12) і B(–2; m). Знайти значення m.
3. Знайти графічно корені рівняння
.
Високий рівень
1. 1) Знайти область визначення функції
і побудувати її графік.
2) Задати функцію
без модуля і побудувати її графік.
2. Скласти формулу лінійної функції, графік якої проходить через точки A(1; 7) і B(2; 11).
3. Побудувати графік функції
.
ЗМІСТ
Передмова 3
Тематичне планування з алгебри у 8 класі (ІІ семестр) 5