Приложение 5
2
- распределение
|
|
| ||||||
|
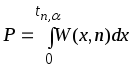
n |
0,01 |
0,02 |
0,05 |
............. |
0,95 |
0,98 |
0,99 |
|
1 |
0,000 |
0,001 |
0,004 |
............. |
3,840 |
5,410 |
6,640 |
|
2 |
0,020 |
0,040 |
0,103 |
............. |
5,990 |
7,820 |
9,210 |
|
3 |
0,115 |
0,165 |
0,352 |
............. |
7,820 |
8,840 |
11,34 |
|
4 |
0,297 |
0,428 |
0,711 |
............. |
9,430 |
11,87 |
13,28 |
|
5 |
0,554 |
0.752 |
1,145 |
............. |
11,07 |
13,38 |
15,09 |
|
6 |
0,672 |
1,134 |
1,635 |
............. |
12,59 |
15,03 |
16,81 |
|
7 |
1,238 |
1,564 |
2,170 |
............. |
14,07 |
16,62 |
18,48 |
|
8 |
1,646 |
2,030 |
2,730 |
............. |
15,51 |
18,17 |
20,10 |
|
9 |
2,090 |
2,530 |
3,320 |
............. |
16,92 |
18,66 |
21,70 |
|
10 |
2,560 |
3,080 |
3,940 |
............. |
18.31 |
21,20 |
23,20 |
|
11 |
3,050 |
3,610 |
4,580 |
............. |
19,88 |
22,80 |
24,70 |
|
12 |
3,570 |
4,180 |
5,230 |
............. |
21,00 |
24,10 |
26,20 |
|
13 |
4,110 |
4,760 |
5,890 |
............. |
22,40 |
25,50 |
27,70 |
|
14 |
4,880 |
5,370 |
6,570 |
............. |
23,70 |
26,80 |
28,10 |
|
15 |
5,230 |
5,980 |
7,280 |
............. |
25,00 |
28,30 |
30,60 |
|
16 |
5,810 |
6,610 |
7,960 |
............. |
26,30 |
28,60 |
32,00 |
|
17 |
6,410 |
7,260 |
8,670 |
............. |
27,60 |
31,00 |
33,40 |
|
18 |
7,020 |
7,810 |
9,390 |
............. |
28,80 |
32,30 |
34,80 |
|
19 |
7,630 |
8,570 |
10,12 |
............. |
30,10 |
33,70 |
36,20 |
|
20 |
8,260 |
8,240 |
10,85 |
............. |
31,40 |
35,00 |
37,60 |
|
21 |
8,900 |
9,920 |
11,58 |
............. |
32,70 |
36,30 |
38,90 |
|
22 |
9,540 |
10,60 |
12,34 |
............. |
33,90 |
37,70 |
40,30 |
|
23 |
10,20 |
11,29 |
13,09 |
............. |
35,20 |
39,00 |
41,80 |
|
24 |
10,86 |
11,99 |
13,85 |
............. |
36,40 |
40,30 |
43,00 |
|
25 |
11,52 |
12,70 |
14,61 |
............. |
37,70 |
41,60 |
44,30 |
|
26 |
12,20 |
13,41 |
15,38 |
............. |
38,80 |
42,90 |
45,80 |
|
27 |
12,88 |
14,12 |
16,15 |
............. |
40,10 |
44,10 |
47,00 |
|
28 |
13,56 |
14,85 |
16,93 |
............. |
41,30 |
45,40 |
48,30 |
|
29 |
14,26 |
15,57 |
17,71 |
............. |
42,60 |
46,70 |
49,60 |
|
30 |
14,95 |
16,31 |
18,49 |
............. |
43,80 |
48,10 |
50,80 |
Приложение 6
F - распределение Фишера для уровня значимости =0,05
|
|
n1 |
| ||||||
|
n2 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
|
4 |
6.39 |
6.26 |
6.16 |
6.09 |
6.04 |
6.00 |
5.96 |
5.91 |
|
5 |
6.19 |
5.05 |
4.95 |
4.88 |
4.82 |
4.76 |
4.74 |
4.68 |
|
6 |
4.53 |
4.39 |
4.28 |
4.21 |
4.15 |
4.10 |
4.06 |
4.00 |
|
7 |
4.12 |
3.97 |
3.87 |
3.79 |
3.73 |
3.88 |
3.63 |
3.57 |
|
8 |
3.84 |
3.69 |
3.58 |
3.50 |
3.44 |
3.39 |
3.34 |
3.28 |
|
9 |
3.63 |
3.48 |
3.37 |
3.29 |
3.23 |
3.18 |
3.13 |
3.07 |
|
10 |
3.48 |
3.33 |
3.22 |
3.14 |
3.07 |
3.02 |
2.97 |
2.91 |
|
12 |
3.26 |
3.11 |
3.10 |
2.92 |
2.85 |
2.80 |
2.76 |
2.68 |
|
16 |
3.01 |
2.85 |
2.74 |
2.66 |
2.59 |
2.54 |
2.48 |
2.42 |
|
20 |
2.87 |
2.71 |
2.60 |
2.52 |
2.54 |
2.40 |
2.35 |
2.28 |
|
30 |
2.69 |
2.56 |
2.42 |
2.34 |
2.27 |
2.21 |
2.18 |
2.08 |
|
40 |
2.81 |
2.45 |
2.34 |
2.25 |
2.18 |
2.12 |
2.07 |
2.00 |
|
50 |
2.56 |
2.40 |
2.29 |
2.20 |
2.13 |
2.07 |
2.02 |
1.95 |
|
100 |
2.46 |
2.30 |
2.18 |
2.10 |
2.03 |
1.97 |
1.92 |
1.85 |
|
200 |
2.41 |
2.26 |
2.14 |
2.05 |
1.98 |
1.92 |
1.87 |
1.80 |
|
|
2.37 |
2.21 |
2.08 |
2.01 |
1.94 |
1.88 |
1.83 |
1.75 |
|
|
n1 | |||||||
|
n2 |
16 |
20 |
30 |
40 |
50 |
100 |
200 |
|
|
4 |
5.84 |
5.80 |
5.74 |
5.71 |
7.70 |
5.66 |
5.65 |
6.63 |
|
5 |
4.60 |
4.56 |
4.50 |
4.46 |
4.44 |
4.40 |
4.38 |
4.36 |
|
6 |
3.92 |
3.87 |
3.81 |
3.77 |
3.75 |
3.71 |
3.69 |
3.67 |
|
7 |
3.49 |
3.44 |
3.38 |
3.34 |
3.32 |
3.28 |
3.25 |
3.23 |
|
8 |
3.28 |
3.15 |
3.08 |
3.05 |
3.03 |
2.98 |
2.96 |
2.93 |
|
9 |
2.98 |
2.93 |
2.86 |
2.82 |
2.80 |
2.76 |
2.73 |
2.71 |
|
10 |
2.82 |
2.77 |
2.70 |
2.67 |
2.64 |
2.59 |
2.56 |
2.54 |
|
12 |
2.60 |
2.54 |
2.46 |
2.42 |
2.40 |
2.35 |
2.32 |
2.30 |
|
16 |
2.33 |
2.28 |
2.20 |
2.16 |
2.13 |
2.07 |
2.04 |
2.01 |
|
20 |
2.18 |
2.12 |
2.04 |
1.99 |
1.96 |
1.90 |
1.87 |
1.84 |
|
30 |
1.99 |
1.93 |
1.84 |
1.79 |
1.76 |
1.69 |
1.66 |
1.62 |
|
40 |
1.90 |
1.84 |
1.74 |
1.69 |
1.66 |
1.59 |
1.55 |
1.51 |
|
50 |
1.85 |
1.78 |
1.69 |
1.63 |
1.60 |
1.52 |
1.48 |
1.44 |
|
100 |
1.75 |
1.68 |
1.57 |
1.51 |
1.48 |
1.39 |
1.34 |
1.28 |
|
200 |
1.69 |
1.62 |
1.52 |
1.45 |
1.42 |
1.32 |
1.28 |
1.19 |
|
|
1.64 |
1.57 |
1.46 |
1.40 |
1.35 |
1.24 |
1.17 |
1.00 |
1Приведенные здесь и далее по тексту далее определения соответствуют ГОСТ 16263-70
2 Смотри Приложение 1
3 Определение понятия коррелированности см. ниже.
4 Большев Л.В., Смирнов Н.И. Таблицы математической статистики. М.,ВЦ АН СССР 1968
5 В дальнейшем под исправленными экспериментальными данными будем понимать результаты наблюдения, из которых исключена систематическая погрешность