Проблемы.

1)

2) Что будет с рядом при t=0 ?

Необходимое условие существования классического решения:

3) Когда ряд (9) сходится равномерно?

Теорема 2.

Пусть и

Тогда ряд (11) сходится абсолютно и равномерно по .

Следствие (о классическом решении задачи).

Пусть и

Тогда формула (9) дает классическое решение задачи (1)-(3).

Пример (безопасность ядерного реактора).

Имеется ядерный реактор с ураном в центре.

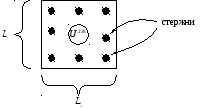
a – коэффициент диффузии нейтронов.

Вопрос:при каких a, L_x, L_y реактор не взорвется?

Сразу производим редукцию: т.к. f=qu, то , гдеудовлетворяет задаче:

Условие отсутствия взрыва:

Решение задачи.

, где V j удовлетворяет задаче:

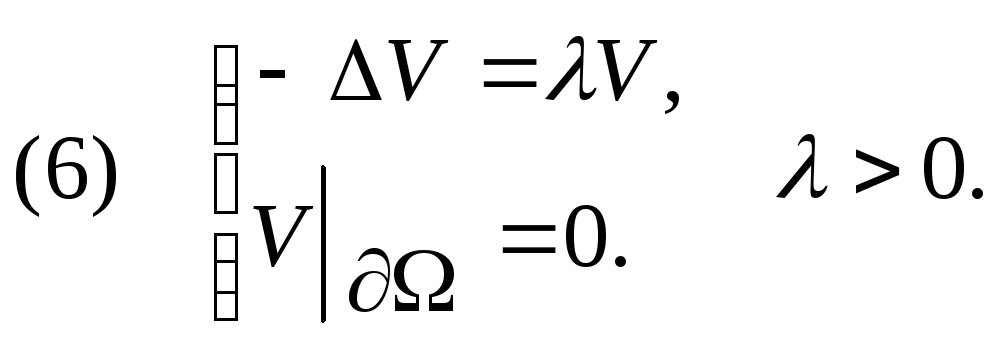
Т.о.

Решаем эту задачу.

X(x)=Acos(_xx) + Bsin(_xx).

X(0)=0=A  A=0.

X(L_x)=0=Bsin(_xL_x), B0  sin(_xL_x)=0  _xL_x= n, n N.

Обозначим

Аналогично

Решение задачи (6):

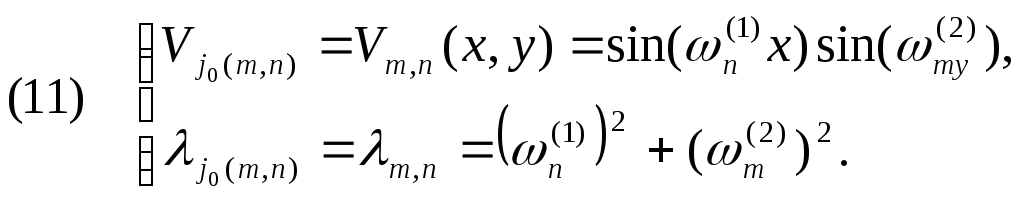
Заметим, что

Подставим (11) в (5), а затем (5) в (4). Т.о. мы получим:

Когда выполняется (*)?

Ответ: .

Т.к. , то достаточным условием выполнения (*) является условие: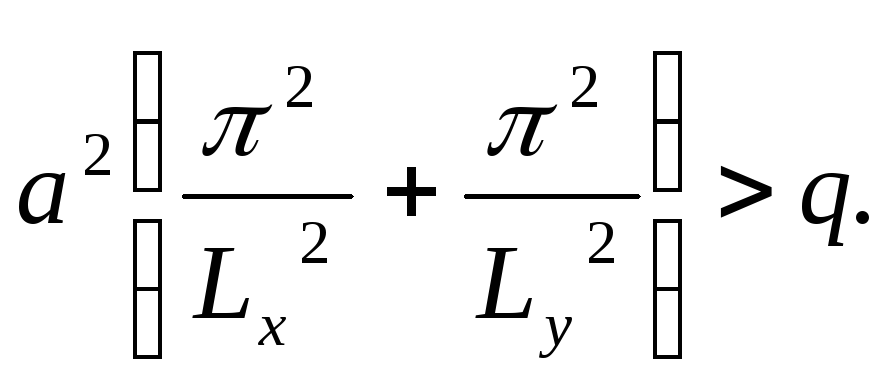

§5. Корректность начально-краевой задачи для уравнения диффузии с краевым условиемI-ого рода

Определение (корректная постановка задачи).

Задача (1)-(3) называется корректно-поставленной, если выполняются следующие три условия:

1) Решение существует в некотором классе функций K₁.

2) Решение единственно в некотором классе K₂. При этом K₁  K₂. .

3)Решение устойчиво (непрерывно зависимо) относительно правой части начальных и граничных условий.

Замечание 1.

Решение представляется в виде: , гдеu_I отвечает задаче с , а функцияu_II –

Замечание 2.

Рассмотрим вопрос непрерывной зависимости функции u_I от  , .

Пусть соответствует задаче с условиямиБудем считать, чтоТогда требуется, чтобыОтвет на этот вопрос следует из принципа максимумов для задачи (1)-(3).

Теорема 1 (принцип максимумов).

Пусть u_I(x,t) u(x,t) ( f  0) – классическое решение задачи (1)-(3).

Тогда наибольшее и наименьшее значения этого решения достигаются либо на нижнеи основании цилиндра ₀ , либо на его боковой поверхности _б ,т.е.

Строгое доказательство этой теоремы смотри в учебнике. Она доказывается от противного.

Эта теорема очевидна с точки зрения сути процесса, а именно с точки зрения второго начала термодинамики.

«Доказательство».

Рассмотрим случай  =1, n=1.

Пусть дано начальное распределение температур ( (x)). Согласно второму началу термодинамики, в дальнейшем энергия может только рассеиваться, т.е. температура только уменьшаться, т.е. максимум не может достигнуться в последующие моменты времени.

Пусть   0. Пусть нам дана температура на концах. В последующем от концов она будет распространяться по всему объему. Опять же, по второму началу термодинамики, где-то посередине она не может стать больше, чем на концах.

Т.о. теорема «доказана».

Теорема 2 (о единственности классического решения).

Пусть f0.

Тогда классическое решение задачи (1)-(3) единственно.

Доказательство.

Предположим противное. Пусть u₁ , u₂ – 2 решения задачи. Положим w=u₁ - u₂.

Тогда w удовлетворяет задаче:

По теореме 1 , что и требовалось.

Теорема 3 (о непрерывной зависимости классического решения).

Пусть f  0.

Тогда классическое решение задачи (1)-(3) непрерывным образом зависит от начальных и граничных условий, а именно:

Доказательство.

Положим . По условию теоремы:и, аналогично,

Согласно теореме 1 , где

Т.о. мы получаем, что

.Теорема доказана.